こんにちは!
それでは今回も化学のお話ししていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(isochoric and isobaric process)
それでは内容に入っていきます!
熱力学第一法則と熱量
まずは、前回お話した熱力学第一法則から始めていきます。
熱力学第一法則とは、内部エネルギーの変化量が、系に与えられた熱量と系にされた仕事の和で表せるというものでした。

詳しくは、こちらの記事を参照してください。
この式を使うと、系が外部へした微小な仕事\(-\rm{d’}\)\(w\)は、\(\rm{d’}\)\(q-\rm{d}\)\(U\)ということになります。
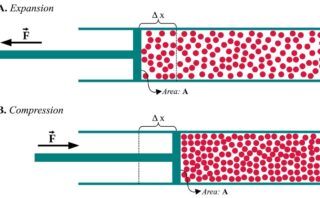
また、↓の図のようなピストンを考えると、\(-\rm{d’}\)\(w\)は\(pA\rm{d}\)\(z\)となります。
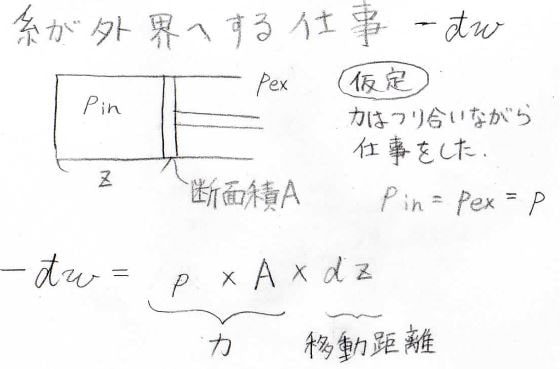
ここで、ピストンが動いている間は常に力が釣り合っているという仮定をしています。
その場合、中と外の圧力は等しく、ここではその値を\(p\)としています。
\(A\)は動く壁の面積、\(\rm{d}\)\(z\)はピストンが外界の方向へ動いた微小距離を指します。
そして、微小な体積変化\(\rm{d}\)\(V\)は\(A\rm{d}\)\(z\)であるため、\(-\rm{d’}\)\(w\)は\(p\rm{d}\)\(V\)と表すことができます。
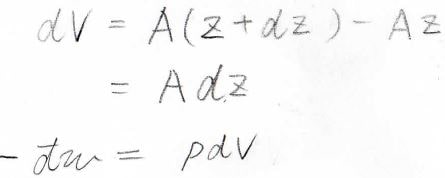
したがって、系にされた仕事\(\)\(w\)は、\(-p\rm{d}\)\(V\)で表されることになります。

これを熱力学第一法則の式に入れると、\(\rm{d}\)\(U=\rm{d’}\)\(q-p\rm{d}\)\(V\)となるため、このときに系に与えられた熱量\(\rm{d’}\)\(q\)は、\(\rm{d}\)\(U+p\rm{d}\)\(V\)だということになります。
定積変化
それでは、以上のことを踏まえて定積変化、すなわち体積一定条件下における内部エネルギーの変化を考えていきましょう。
ちなみに定積変化は定容変化、等積変化とも言います。
体積一定下で、系へ与えられた熱量を\((\rm{d’}\)\(q)_V\)と表すことにすると、これは\((dU)_V\)\(+p\rm{d}\)\(V\)となり、体積一定で\(\rm{d}\)\(V=0\)となるので、結局内部エネルギーの変化だけになります。
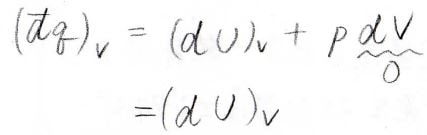
ここで、熱容量というものを定義します。
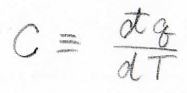
意味としては、単位温度分だけ温度上昇させるために必要な熱量であり、微小な熱量\(\rm{d’}\)\(q\)を微小な温度変化\(dT\)で割ったものになります。
今熱量は内部エネルギーの変化量と等しいため、定積熱容量\(C_V\)は体積一定下で内部エネルギーを温度で偏微分した値となります。
定圧変化
続いて定圧変化、すなわち圧力一定条件下における内部エネルギーの変化を考えていきましょう。
これも補足ですが、定圧変化は等圧変化とも言います。
圧力一定下において系へ与えられた熱量\((\rm{d’}\)\(q)_p\)は\((\rm{d}\)\(U)_p\)\(+p\rm{d}\)\(V\)となります。
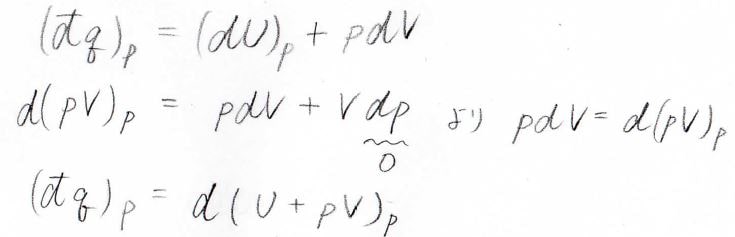
ここで、\(pV\)の全微分を考えると\(p\rm{d}\)\(V+V\rm{d}\)\(p\)であり、今は\(\rm{d}\)\(p=0\)なので、\(p\rm{d}\)\(V=\rm{d}\)\((pV)_p\)となります。
全微分についてはこちらを参照してください。

これを上の式に代入すると、結局熱量は内部エネルギー\(U\)に圧力と体積の積\(pV\)を足した値の変化量に等しくなります。
したがって、この\(U+pV\)を新たな状態量\(H\)として定義すると、定圧熱容量\(C_p\)は圧力一定下で\(H\)を温度で偏微分した値となります。
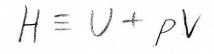
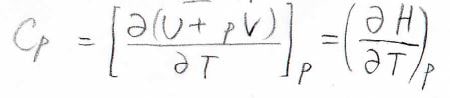
ここで、状態量\(H\)はエンタルピーと言います。
このエンタルピーというのは、化学をやるうえでとても重要な量となります。
同じことを繰り返しますが、圧力一定下でのエンタルピー変化は、系へ与えられた熱量と等しくなります。
化学反応の多くはその前後で温度や圧力の変化はほとんど起こっていないと考えることができるため、例えば反応によって発生した熱量はエンタルピーの変化量として考えることができます。
また、発熱反応はより熱力学的に安定な方向への反応ですが、この時エンタルピー変化はマイナスの値になります。
したがって、エンタルピーとはその系、あるいは化合物の熱力学的な安定性を表す値だということになります。
詳しくはまた別の記事でやっていくので、ひとまず頭の片隅においてもらえればと思います。
まとめ
それでは、今回の内容は以上なので、最後おさらいをやって終わります。
今回は定積変化、定圧変化における内部エネルギー変化と熱容量を考えました。
系へ与えられる微小な仕事は\(-pdV\)となるため、系へ与えられる熱量は熱力学第一法則より\(dU+pdV\)となります。
これを使うと、まず定積変化において系へ与えられる熱量は内部エネルギーの変化量と等しくなります。
そして単位温度を上昇させるのに必要な熱量を熱容量とすると、定積熱容量は体積一定下で内部エネルギーを温度で偏微分した値になります。
定圧変化においては、内部エネルギー\(U\)に圧力と体積の積\(pV\)を足したエンタルピーの変化量が系へ与えられた熱量になります。
定圧熱容量は圧力一定下でエンタルピーを温度で偏微分したものです。
化学反応の多くはその前後で圧力変化がほとんどないと考えることができるため、エンタルピー変化は反応熱と等しくなり、エンタルピー自身は系の安定性を表す指標になります。
それではどうもありがとうございました!