こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(gas mixture)
それでは内容に入っていきます!
部分モル量
始めに、部分モル量の概念についてお話します。
部分モル体積
ここでは、水を例に説明していきます。
まずある温度と圧力のもと、\(1\ \rm{mol}\)の水は液体で、その体積が\(18\ \rm{mL}\)だったとします。
これを大量の水の中に注ぐと、当然ながら、全体の体積が\(18\ \rm{mL}\)だけ増加します。
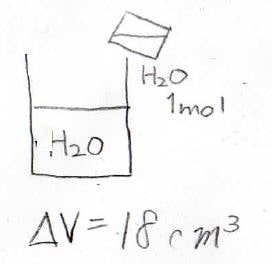
このとき、新たに加えた水が全体に占める体積は、\(18\ \rm{mL}\)です。
では、大量のエタノールの中に水を\(1\ \rm{mol}\)入れるとどうなるでしょうか?
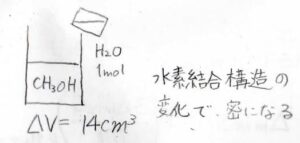
このときの全体の体積変化は、わずか\(14\ \rm{mL}\)と純粋なときの体積より小さくなります。
これは、水素結合によってできた立体的な構造の違いが原因です。
このとき、水が全体に占める体積は\(\rm{14\ mL}\)になります。
水が全体に対して\(1\ \rm{mol}\)あたりどれだけの体積を占めるのかというのは、こちらの偏微分の式で与えられ、これを部分モル体積と言います。
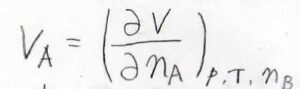
\(V\)が全体の体積、\(n_\rm{A}\)は加えた水の物質量、\(p\)は圧力、\(T\)は絶対温度、\(n_\rm{B}\)は水もしくはエタノールの物質量です。
この\(V_\rm{A}\)の値は、水分子の周りにどれだけエタノールが存在しやすいのかという確率によって変化するため、エタノールと水の組成に依存します。
エタノールのモル分率を\(x_\rm{B}\)として、横軸を\(x_\rm{B}\)、縦軸を\(V_\rm{A}\)とすると、このような依存性になります。

最初の例のように、すべて水だったときなど単成分系については、部分モル体積とモル体積は等しくなります。
そして、水とエタノールの系に限らず、一般的な混合系についても、部分モル体積は下のように定義されます。
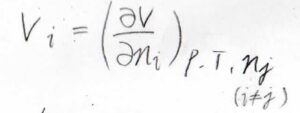
着目している成分以外のすべての成分の物質量を固定して、全体の体積を物質量について偏微分します。
横軸に\(n_i\)、縦軸に\(V\)をとると、このグラフの傾きがその組成における部分モル体積になります。
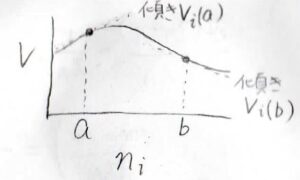
物質を加えることで全体の体積が減少する場合もあるため、\(V\)は常に正でも、\(V_i\)が負の値になることがあります。
温度と圧力を一定とすると、全体の体積は各成分の物質量にのみ依存する関数となりますが、その全微分\(\displaystyle \rm{d}\)\(V\)は、\(\displaystyle V_1\rm{d}\)\(n_1+V_2\rm{d}\)\(n_2+\cdots\)と書けます。
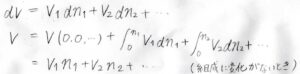
これを全体の物質量が\(0\)のときから現在の状態まで積分します。
物質量が\(0\)のときの体積である\(V(0,0,…)\)は、当然ながら\(0\)です。
部分モル体積は、組成には依存しますが、全体の物質量には依存しないため、組成をそのままにしたまま積分をしたとすれば、各成分の部分モル体積を定数として、積分の前に出すことができます。
したがって、全体の体積\(V=V_1n_1+V_2n_2+…\)と書くことができます。
つまり、組成とその組成における部分モル体積さえわかっていれば、全体の物質量によって全体の体積もわかるという関係になります。
そして、体積は経路に依存しない状態量であるため、各成分を混ぜる順番などは関係なく、最終的な組成だけが重要になります。
部分モルギブズエネルギー
ここまでやってきたことは、示量性の物質量でさえあれば、体積以外の量についても考えることができます。
例えば、以前から紹介している化学ポテンシャルもギブズエネルギーの部分モル量です。
化学ポテンシャル\(\mu\)は温度、圧力、そして着目している成分以外のすべての成分の物質量を固定して、全体のギブズエネルギー\(G\)をその成分の物質量について微分したものです。
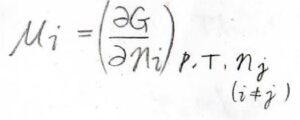
単成分系であれば、ギブズエネルギーが物質量に比例するため、微分するのと物質量で割るのとで、結果は同じになります。
混合系のギブズエネルギー\(G\)の全微分\(\rm{d}\)\(G\)は、下の形で与えられます。

温度と圧力が一定のとき、非膨張の最大仕事\(\rm{d’}\)\(w_\rm{add, max}\)は\(\rm{d}\)\(G\)と等しくなるため、\(\rm{d’}\)\(w_\rm{add, max}\)\(=\mu_1\rm{d}\)\(n_1+\mu_2\rm{d}\)\(n_2+\cdots\)という関係になります。
それで、温度と圧力が一定、さらに組成に変化がなかったものとすると、先ほど同様に全体のギブズエネルギー\(G=\mu_1n_1+\mu_2n_2+\cdots\)と書けます。
つまり、組成とその組成における化学ポテンシャルがわかっていれば、全体の物質量によって全体のギブズエネルギーがわかります。
ただし、ここで少し変なことが起こります。
この式について全微分を書くと、\(n_1\rm{d}\)\(\mu_1\)のような項が出てきます。
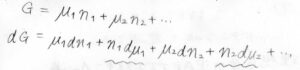
ギブズエネルギーは状態量であり、この式と最初に考えた全微分の式はどちらも正しい式のはずなので、\(\displaystyle \sum_i n_i\rm{d}\)\(\mu_i=0\)という式が成り立つことになります。
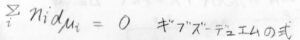
この式は、ギブズ-デュエムの式と呼ばれます。
その意味は、混合系における1つの成分の化学ポテンシャルは、ほかの成分の化学ポテンシャルと独立に変化できないということです。
例えば、成分\(\rm{A}\)と成分\(\rm{B}\)の2成分系について、この式を変形すると\(\rm{d}\)\(\mu_\rm{A}\)\(\displaystyle =-\frac{n_\rm{B}}{n_\rm{A}}\rm{d}\)\(\mu_\rm{B}\)となるので、一方の化学ポテンシャルが増大すると、もう一方は減少する関係になっていることがわかります。
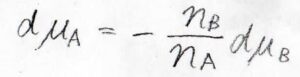
部分モル体積についても、このようにギブズ-デュエムの式が書けます。
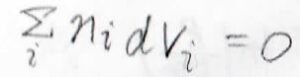
実験的には、一方の成分の部分モル体積を測定し、その結果からもう一方の成分の部分モル体積を求める際にこの式が使われます。
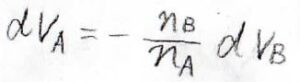
部分モル内部エネルギー、部分モルエンタルピー、部分モルヘルムホルツエネルギー
ここで少し話が変わりますが、ギブズエネルギー\(G\)は、内部エネルギー\(U\)を使って\(U+pV-TS\)と書けるため、\(U=G-pV+TS\)となります。
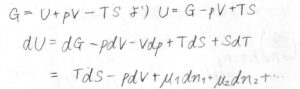
その全微分\(\rm{d}\)\(U\)は\(T\rm{d}\)\(S-p\rm{d}\)\(V+\mu_1\rm{d}\)\(n_1+\mu_2\rm{d}\)\(n_2+\cdots\)となります。
つまり、\(\displaystyle \mu_i=(\frac{\partial U}{\partial n_i})_{S, V, n_j}\)となるため、化学ポテンシャルは部分モルギブズエネルギーであると同時に、内部エネルギーの組成依存性も表していることになります。
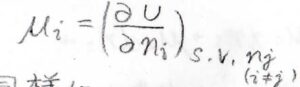
同様にエンタルピー\(H\)、ヘルムホルツエネルギー\(A\)の組成依存性も化学ポテンシャルで書くことができます。
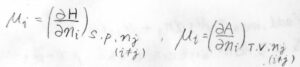
これが、化学という分野において、化学ポテンシャルが重要とされる根本的な理由です。
混合ギブズエネルギー
最後に、2種類の理想気体を混合したときのギブズエネルギー変化について考えます。
温度と圧力を一定としたまま、2つの気体を隔てている仕切りを外して、長時間放置します。
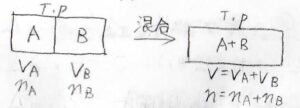
このとき、化学ポテンシャルは、それぞれが純粋なときの式を使って書くことができます。
つまり、化学ポテンシャルは純粋なときのモルギブズエネルギーに等しく、温度と圧力の関数になります。
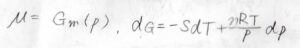
さらに、理想気体の状態方程式から体積\(V\)を\(\displaystyle \frac{nRT}{p}\)と書くことができるため、ギブズエネルギーの全微分\(\rm{d}\)\(G=-S\rm{d}\)\(\displaystyle T+\frac{nRT}{p}\rm{d}\)\(p\)となります。
ただし、混合系における\(p\)は、全圧ではなくてその成分の分圧として考えます。
温度を一定としたまま、モルギブズエネルギーを積分によって求めると、\(\displaystyle \mu=\mu^\circ+RT\ln{(\frac{p}{p^\circ})}\)という式が得られます。
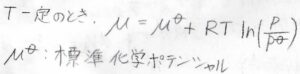
ここで、\(p^\circ\)は標準圧力、\(\mu^\circ\)は標準圧力におけるモルギブズエネルギーを指し、標準化学ポテンシャルと呼びます。
そして2つの気体について、それぞれの化学ポテンシャルから混合ギブズエネルギー\(\Delta_\rm{mix}\)\( G\)を求めると、最終的に\(\Delta_\rm{mix}\)\( G=n_\rm{A}\)\(\displaystyle RT\ln{(\frac{p_\rm{A}}{\mathit{p}})}+n_\rm{B}\)\(\displaystyle RT\ln{(\frac{p_\rm{B}}{\mathit{p}})}\)となります。

ここで、\(p_\rm{A}\)と\(p_\rm{B}\)は分圧で、必ず全圧\(p\)よりも小さくなります。
それぞれのモル分率を\(x_\rm{A}\)、\(x_\rm{B}\)とすると、ドルトンの法則より、\(p_\rm{A}\)\(=x_\rm{A}\)\(p\)、\(p_\rm{B}\)\(=x_\rm{B}\)\(p\)と書けます。
\(\Delta_\rm{mix}\)\( G\)をモル分率を使って書くと、\(\Delta_\rm{mix}\)\( G=nRT(x_\rm{A}\)\(\ln{x_\rm{A}}+x_\rm{B}\)\(\ln{x_\rm{B}})\)となります。
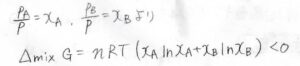
ここで、\(n\)は全体の物質量で、\(n=n_\rm{A}\)\(+n_\rm{B}\)です。
モル分率は\(0\)より大きく\(1\)より小さい値をとるため、対数部分はかならず負の値となります。
したがって、気体の混合によってギブズエネルギーは減少するということになります。
このことは、理想気体がどんな組成であっても自発的に混ざり合うということを説明しています。
また、\(\displaystyle (\frac{\partial G}{\partial T})_{p, n_\rm{A}, \mathit{n}_B}=-\mathit{S}\)より、混合エントロピー\(\Delta_\rm{mix} \)\(\displaystyle S=-(\frac{\partial \Delta_\rm{mix} \mathit{G}}{\partial \mathit{ T}})_{\mathit{p, n}_\rm{A}, \mathit{n}_\rm{B}}\)となります。
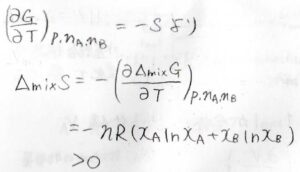
上の式を代入すると、\(\Delta_\rm{mix}\)\( S=-nR(x_\rm{A}\)\(\ln{x_\rm{A}}+\mathit{x}_\rm{B}\)\(\ln{x_\rm{B}})\)と求められます。
かっこの中が負の値で、それにマイナスが付いているので、この値の符号は正になります。
外界との熱のやり取りはないので、この値は外界も含んだ孤立系としてのエントロピー変化と等しくなります。
そして、混合エンタルピー\(\Delta_\rm{mix}\)\( H=\Delta_\rm{mix}\)\( G+T\Delta_\rm{mix}\)\( S=0\)となります。
これは、理想気体では分子間相互作用を考えていないためです。
横軸を\(\rm{A}\)のモル分率として、グラフを書くとこうなります。
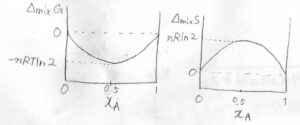
左が混合ギブズエネルギーで、右が混合エントロピーです。
理想気体であれば、どちらも\(x_\rm{A}\)\(=0.5\)のところで極値をとります。
それぞれの極値の値は、\(-nRT\ln{2}\)、\(nR\ln{2}\)となります。
そして、グラフの両端、すなわち\(x_\rm{A}\)を\(0\)と\(1\)にそれぞれ近づけていったときの傾きの極限は、ギブズエネルギーについて\(-\infty\)、エントロピーについて\(\infty\)となります。
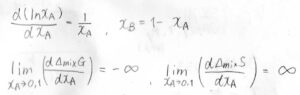
このことは、分子間相互作用がある系について考えるときに非常に重要な意味をもちますので、ぜひ知っておいてください。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




