こんにちは!
今回も化学のお話やっていきます。
今回のテーマはこちら!
動画で使ったシートはこちら(perturbation)
摂動法の計算条件
まず、摂動法がどういうものか、おさらいします。
摂動法ではまず、ハミルトニアンを下のように置き換えます。

\(\hat{H}’\)というのが補正項、\(\hat{H}_0\)は補正前のハミルトニアンです。
ここで、\(g\)は定数です。
\(g=0\)は無補正を表し、そこから\(g\)が増加するとともに、波動関数やエネルギーも徐々に変化していき、\(g=1\)が補正後を表します。
そして、ハミルトニアンに補正を加えると、エネルギーと波動関数も変わります。
ここでは、\(g\)のべき級数の形で考えます。
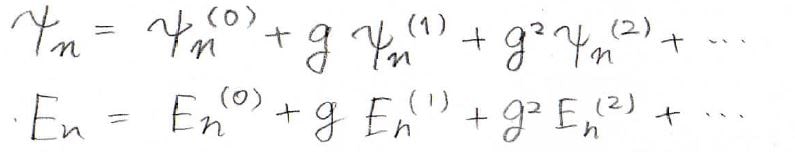
ここで、\(n\)は量子数、かっこの中の数字が補正項の次数です。
\(\displaystyle (0)\)は補正してないという意味なので、\(\psi _n^{(0)}\)と\(E_n^{(0)}\)は補正前の値と一致します。
シュレディンガー方程式の係数比較
以上の値をシュレディンガー方程式に入れてみます。

すると、両辺が\(g\)のべき級数になりますが、この等式が常に成り立つためには、各項の係数が同じにならないといけません。
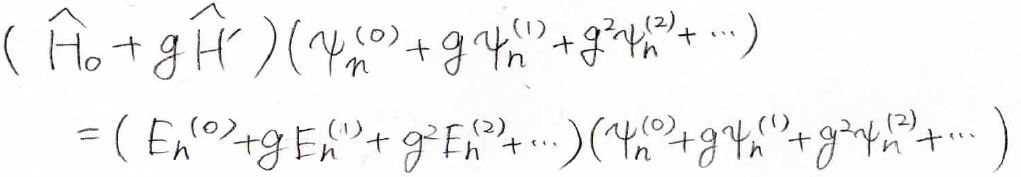
例えば、\(g^0\)の係数を取り出してみると、\(\hat{H}_0\psi_n^{(0)}=E_n^{(0)}\psi_n^{(0)}\)となりますが、補正前のシュレディンガー方程式と同じなので、これは常に成り立ちます。

同様に、\(g^1\)については、下記の等式が成り立ちます。

\(g^2\)についても、下記のようになります。

波動関数とエネルギーの補正項
直交系の線形結合を利用
ここから波動関数とエネルギーの補正項を考えるためには、補正前の波動関数が直交性を満たすことを利用します。
例えば、一次独立な2つの二次元ベクトルがあったときに、平面上の任意のベクトルは、この2つのベクトルの線形結合として表すことができます。

同様に、互いに直交している\(\psi_n^{(0)}\)の線形結合で任意の波動関数を表すことができます。
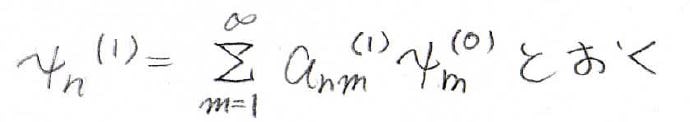
ここでは係数部分を\(a_{nm}^{(1)}\)として、上記のように表すことにします。
エネルギーの一次補正項
\(g^1\)についての等式に、上式を代入します。
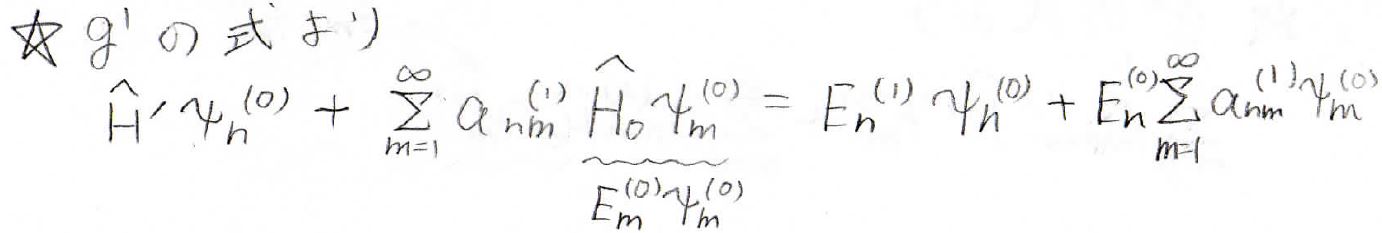
ここで、\(\hat{H}_0\psi_n^{(0)}\)の部分は、補正前のエネルギー\(E_n^{(0)}\)が固有値になります。
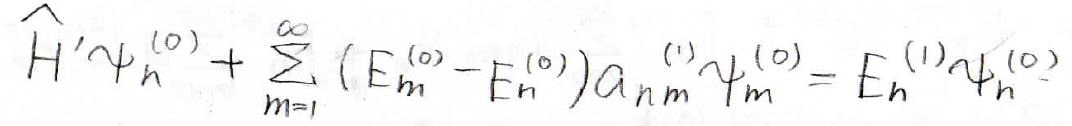
そして、この式の両辺に左から\(\psi_n^{(0)\ast}\)をかけて、全空間について積分します。
まず、左辺だけやってみましょう。

ここで第二項目に注目すると、\(E_n^{(0)}\)と\(a_{nm}^{(1)}\)は定数なので、積分の外に出すことができます。
そして、\(\psi_n^{(0)}\)は直交性を満たしているので、\(n\)と\(m\)が異なる場合、この積分は\(0\)になります。
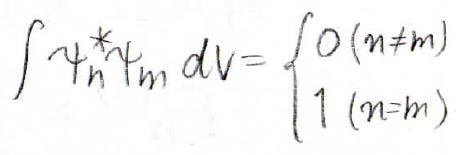
\(n\)と\(m\)が等しい場合は、\(\displaystyle E_m^{(0)}-E_n^{(0)}=0\)になります。
したがって、第二項は\(0\)となります。
一方、規格化条件より右辺は、\(E_n^{(1)}\)となります。
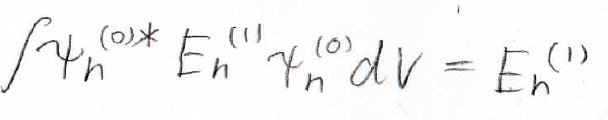
最終的には、下の式が得られます。
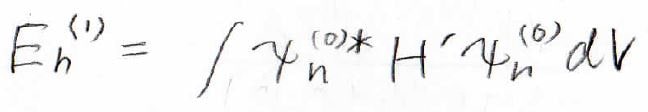
これは、エネルギーの一次の補正項が補正前の波動関数とハミルトニアンの補正項から計算できることを表しています。
波動関数の一次補正項
続いて、波動関数の補正も考えていきましょう。
先ほど\(\psi _n^{(0)\ast}\)をかけたところを\(\psi_m^{(0)\ast}\)に変えて、また左からかけて積分します。
すると、まず左辺は下のようになります。
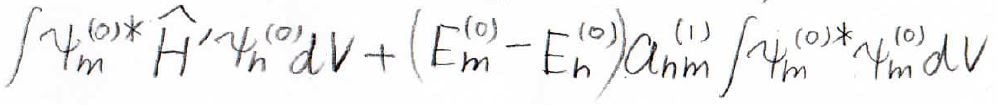
また、右辺は直交性より\(0\)となります。

左辺が\(\displaystyle 0\)となることから、\(a_{nm}^{(1)}\)は下のように書けます。
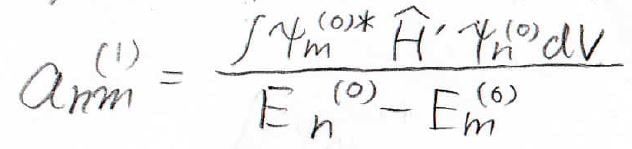
\(a_{nm}^{(1)}\)がすべてわかれば\(\psi_n^{(1)}\)、すなわち波動関数の一次の補正項がわかったことになります。
エネルギーの二次補正項
補正項は無限にあるので、すべてをやりつくすことはできませんが、、エネルギーの二次の補正項を導出して終わります。
まず、\(\psi_n^{(2)}\)も補正前の波動関数の線形結合で書けるものだと考えます。
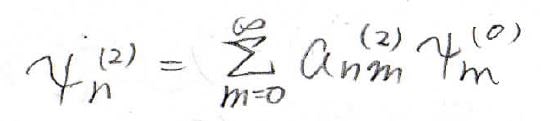
これを\(g^2\)についての等式に代入すると、下記のようになります。
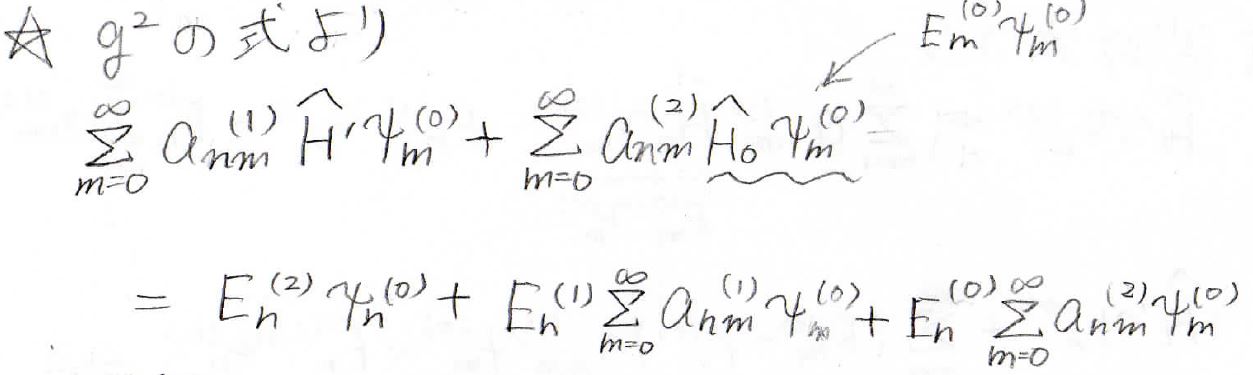
左から\(\psi_n^{(0)\ast}\)をかけて積分すると、先ほどのようなキャンセルが左辺の第二項と右辺の第三項で起こります。
そして、右辺の第二項を移項して、\(\displaystyle E_n^{(1)}=\int \psi_n^{(0)\ast}\hat{H’}\psi_n^{(0)} \rm{d}\mathit{V}\)を代入すると、左辺の\(\displaystyle \sum\)の中で\(n=m\)の場合だけキャンセルします。
さらに、\(\displaystyle a_{nm}^{(1)}\)の式を代入すれば、エネルギーの二次の補正項は、下のように求められます。
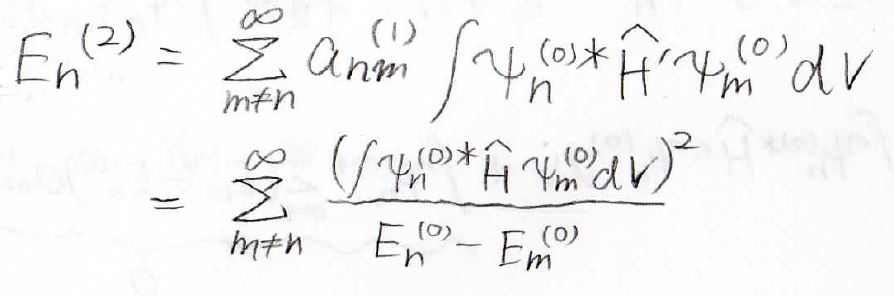
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




