こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(Raman spectroscopy)
それでは内容に入っていきます!
ラマン散乱
前回は、マイクロ波を使って純回転遷移を観測する方法について、お話ししました。
こちらの記事を参照してください。

この方法では、分子に電磁波を照射して、透過光の強度を測ります。
照射する電磁波の波長を変えていき、ちょうど回転準位間のエネルギー差に相当する波長になったときに、光の吸収と放出の両方が起こり、実質の吸収分だけ透過光の強度が減少します。
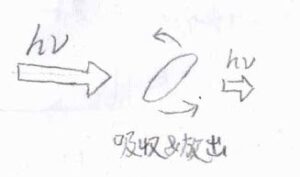
強度を測定する透過光の波長は、入射光の波長と同じです。
対して、今回のテーマであるラマン分光法では、入射光の波長を固定して、分子から散乱される光の強度を測定します。
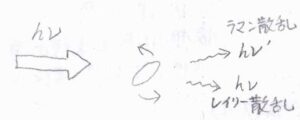
散乱光の波長は、入射光と同じものもありますが、異なるものも出てきます。
まず、波長が変化しない散乱は、レイリー散乱と言います。
電磁波の波長に対して、散乱体がとても小さいときに起こる散乱です。
波長が短いほど、また分子が大きいほど散乱高強度は大きくなります。
空が青く見える理由にもなっています。
ちなみに、散乱体が波長に対してある程度以上大きくなると、ミー散乱という散乱になります。
強度が波長にほとんど依存しないため、白色光の散乱光は白く見えます。
コロイドのチンダル現象はミー散乱です。
話は逸れましたが、入射光と波長が変化して光が散乱される現象のことをラマン散乱といいます。
その原理は、まず遷移前の分子が光を吸収して、ある状態に励起されます。

それから、この状態から別の状態へと緩和が起こります。
緩和した後の状態は、必ずしも遷移前の状態と一致するとは限らないため、入射光のエネルギーに遷移前後のエネルギー差が加算されて、それに相当する波長の散乱光が観測されることになります。
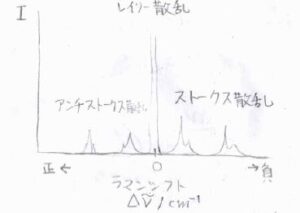
波長が長くなる散乱をストークス散乱、短くなる散乱をアンチストークス散乱といいます。
中間の状態は、仮想状態と呼ばれており、実際ここにエネルギー準位がなかったとしても、ラマン散乱は起こります。
そのときには、複数の振動状態や電子状態の組み合わせとして解釈されます。
入射光のエネルギーだけ励起されたところの近傍に実際のエネルギー準位が存在していた場合には、著しく散乱光の強度が大きくなることが知られており、これを共鳴ラマン散乱といいます。
共鳴ラマン散乱を用いた分光法では、酵素の中の活性中心など、ある一部分の結合について調べることも可能です。
回転ラマン分光法の選択律
ラマン散乱は、前回お話しした純回転遷移と機構が異なり、選択律も異なるものになります。
選択概律
回転ラマン分光法の選択概律は、分子の分極率に異方性があるということです。
分子に一様な外部電場をかけると、その方向に応じて分極が起こります。
その分極によって生じた誘起双極子モーメント\(\boldsymbol{\mu}\)と外部電場\(\boldsymbol{E}\)は向きが平行となるため、\(\alpha\)を定数として、\(\boldsymbol{\mu}=\alpha \boldsymbol{E}\)と書けます。
この\(\alpha\)を分極率と言います。
この分極率は、回転子が球対称ではないとき、方向依存性をもつことになります。
例えば、水素分子のような等核二原子分子は、永久双極子モーメントをもたないため、純回転不活性となりますが、回転ラマン活性となります。
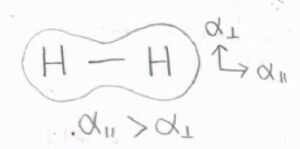
これは、主軸方向に電場がかかっているときと、主軸に対して垂直な方向に電場がかかっているときで、分極の度合いに差が生じるためです。
ほかの例を見てみると、分子が属する点群がラマン活性の判別に役立つことがわかります。
点群については、こちらを参照してください。

例えば、すべての単原子分子は全回転群、四塩化炭素は正四面体群、六フッ化硫黄は正八面体群です。
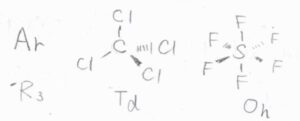
これらの分子は、球対称回転子であり、分極率が方向によって変化しないため、回転ラマン不活性となります。
一方\(C_\rm{\infty v}\)群の塩化水素や\(D_\rm{\infty h}\)群の二酸化炭素、\(C_\rm{3v}\)群のアンモニアなどは、分極率が方向依存性をもつため、回転ラマン活性となります。
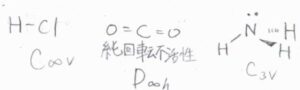
二酸化炭素も水素分子と同様に、永久双極子モーメントをもっていないため純回転不活性ですが、回転ラマンは活性になります。
個別選択律
個別選択律は、まず直線型回転子について回転量子数\(J\)の変化\(\Delta J\)が\(0\)、\(+2\)、\(-2\)のいずれかになります。

\(0\)がレイリー散乱、\(+2\)がストークス散乱、\(-2\)がアンチストークス散乱に対応します。
対称回転子の場合は、さらに\(\Delta J=\pm 1\)の遷移も起こります。
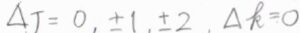
もう1つの回転量子数\(k\)はレイリー散乱、ラマン散乱によって変化しません。
ここでは、個別選択律の古典的な起源を説明するにとどめます。
二原子分子に電磁波を照射したとき、電場の振幅を\(E_0\)、角周波数を\(\omega_\rm{i}\)として、誘起双極子モーメントの大きさ\(\mu_\rm{ind}\)を考えると、\(\alpha E_0 \cos{(\omega_\rm{i} \mathit{t})}\)となります。
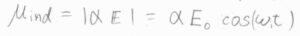
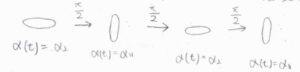
\(\alpha\)に方向依存性があるので、分子の回転周期に応じた\(\alpha\)の変化も考えます。
振動の中心は2方向の分極率の平均で\(\alpha_0\)とし、振幅は分極率差を\(2\)で割った値で、これを\(\Delta \alpha\)と表すことにすると、\(\alpha(t)=\alpha_0+\Delta \alpha \cos{(2\omega_\rm{R} \mathit{t})}\)と書けます。

ここで\(\omega_\rm{R}\)は、分子の古典的な回転運動の角周波数です。
\(\cos\)の中が\(2\omega_\rm{R}\)\( t\)となっているのは、1回転につき分極率のサイクルは2周するということを反映しています。
これが個別選択律\(\Delta J=\pm 2\)の古典的な起源になります。
上の\(\alpha\)に\(\alpha(t)\)を代入して整理すると、遷移双極子モーメントは3つの波の足し合わせとして書けるということになります。
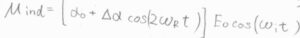
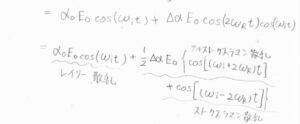
角周波数が入射光のものと一致するものが、レイリー散乱に対応します。
角周波数が入射光のものより小さくなるのがストークス散乱で、大きくなるのがアンチストークス散乱です。
回転ラマンスペクトル
ここからは、直線型回転子の回転ラマンスペクトルの概形を考えていきます。
ここでは、遠心ひずみを考えていません。
\(J+2\leftarrow J\)のときのラマン散乱光の波数は、入射光の波数\(\tilde{\nu}_\rm{i}\)と回転定数\(\tilde{B}\)を使って、\(\tilde{\nu}_\rm{i}\)\(-2\tilde{B}(2J+3)\)となります。
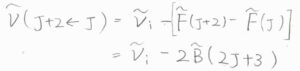
隣り合うスペクトル線の間隔は、\(4\tilde{B}\)となります。
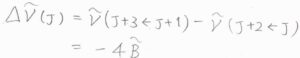
ただし、\(2\leftarrow 0\)の線とレイリー散乱の線の間隔だけは\(6\tilde{B}\)になります。
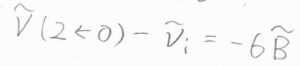
\(J-2\leftarrow J\)の場合は、ラマン散乱光の波数が\(\tilde{\nu}_\rm{i}\)\(+2\tilde{B}(2J+1)\)となります。
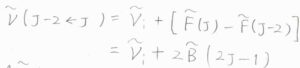
スペクトル線どうしの間隔は、\(\Delta J=+2\)のときと変わりません。
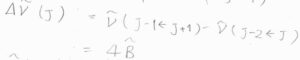
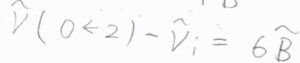
以上のことより、回転ラマンスペクトルの概形はこのような形になります。
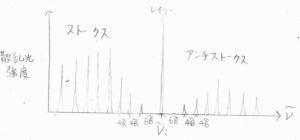
横軸が散乱光の波数で、縦軸が散乱光の強度です。
一般的に、レイリー散乱光の強度に比べると、ラマン散乱光の強度はとても小さいです。
強度には、分極率差や遷移前後の占有数差が影響します。
核統計
ただ実際のスペクトルの概形を理解するには、これだけでは不十分なことがあります。
例えば、二酸化炭素の回転ラマンスペクトルでは、\(J\)が奇数のときのスペクトル線が消失するということが知られています。
この現象は、パウリの原理から説明されます。
二酸化炭素分子を半回転させるという操作は、2つの酸素原子のラベルを交換する操作と同じになります。

電子など半整数のスピンをもつフェルミ粒子の交換では、全波動関数の符号が変化します。
対して、整数のスピンをもつボース粒子の交換では、全波動関数の符号は変化しません。
これがパウリの原理です。
\(^{16}\rm{O}\)の原子核は、スピンが\(0\)のボース粒子であることから、半回転により全波動関数の符号が変わってしまうようなときに、分子はその回転状態をとれなくなり、スペクトル線が消失します。
\(J\)が小さいときの球面調和関数を考えると、\(J\)が\(0\)や\(2\)のときには、半回転させても符号は入れ変わらないので、遷移は許容されます。

\(J=1\)のときには、半回転で符号が逆になるため、禁制となります。
さらに大きな\(J\)についても、ラベルを交換したときの全波動関数は、交換前の全波動関数の\((-1)^J\)倍と書けるため、\(J\)が奇数のときにスペクトル線が消失するということになります。
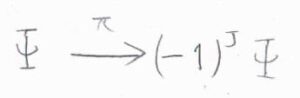
このように、パウリの原理による回転状態の選択的な占有のことを核統計と言います。
回転によりラベルの交換が起こる分子については、核統計を考慮する必要があります。
スペクトル線が消失するのは、核スピンが\(0\)であるときのみであり、一般的には、核スピンの向きの組み合わせの数に応じて、スペクトル線の強度を複雑に変化させます。
例えば、2つの等価な\(1/2\)の核スピンをもつ水素分子では、半回転により全波動関数の符号が反転する必要があります。
2つの核スピンが平行であるときには、これら3つのスピンの組み合わせが考えられますが、ラベルを交換してもスピン状態が変化しないため、回転で符号が反転しなければならず、\(J\)は奇数である必要があります。
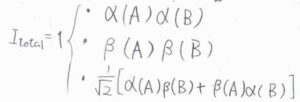
この状態にある水素分子をオルト水素と言います。
対して、スピンが対をなす場合は、1通りのスピン状態が考えられ、\(J\)は偶数をとることになります。
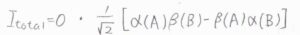
これをパラ水素と呼びます。
相対的な配向が異なる核スピンの交換は非常に遅く、非常に低い温度でもオルト水素は回転し続けます。
実質的に\(J=1\)の状態が基底状態となり、零点エネルギーをもつことになります。
回転ラマンスペクトルの概形は、こちらのようになります。

\(J\)が奇数をとる場合の数は偶数をとる場合の数の\(3\)倍となるため、\(J\)が奇数のときに相対的に大きなピークが現れます。
その結果、強いピークと弱いピークが交互に並んで、観測されることになります。
一般的に、2つの等価な核スピン\(I\)をもつ等核二原子分子で、\(J\)が奇数の場合の数と偶数の場合の数の比は、次のようになります。

まず、核スピンが半整数の場合は、\(\displaystyle \frac{I+1}{I}\)となり、\(J\)が奇数のときの強度が相対的に大きくなります。
核スピンが整数のときには、\(\displaystyle \frac{I}{I+1}\)となり、\(J\)が偶数のときの強度が大きくなります。
その特別な例として、\(I=0\)のときにこの比が\(0\)となり、\(J\)が奇数のピークは観測されなくなります。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!