こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマは、こちら!
動画はこちら↓
動画で使ったシートはこちら(point cloud 1、point cloud 2)
それでは内容に入っていきます!
点群とは?
まず、点群とは何かからお話しします。
点群とは、どんな対称操作によっても動かない共通の点を有するものに存在する対称要素の集合です。
例えば、水分子の酸素原子やアンモニア分子の窒素原子は、回転させても鏡映をとっても動きようがないです。

どんな対称操作によっても動かない共通の点とは、つまりこれらのことで、並進操作は考えることができません。
その条件下で立体、特に分子がもつ対称要素の集合を点群と言います。
同じ点群に属する分子は同じ対称性を持っていることになりますから、これで相互作用を考えられるということです。
点群のフローチャート
それで、点群の種類は無限にあるわけではないので、こんなフローチャートに則って、その分子がどの点群に属するのか機械的に分類することができます。
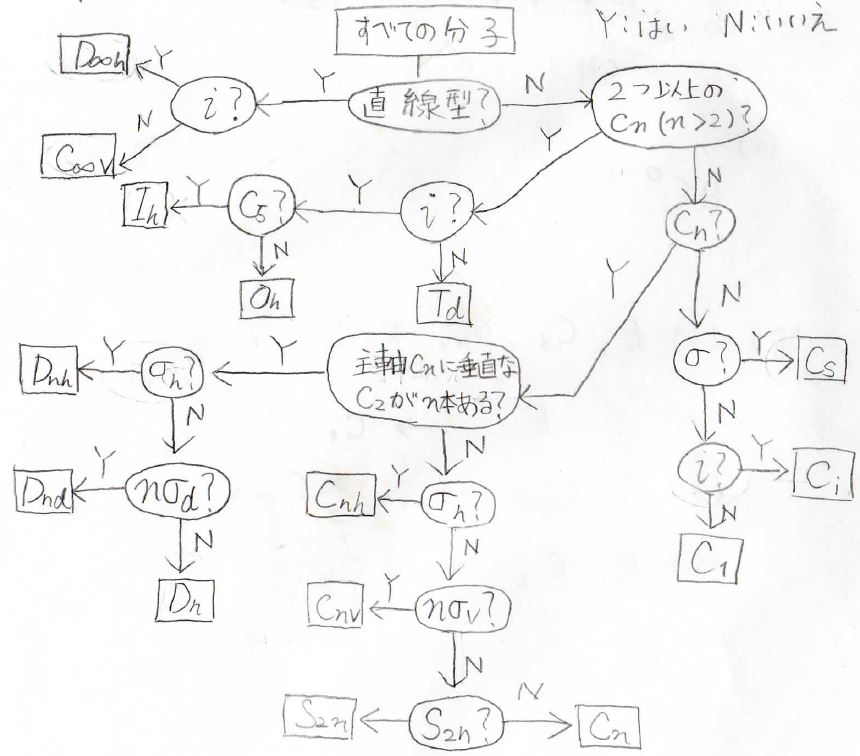
お持ちの無機化学や物理化学の教科書にも、似たようなものが載っていると思うので、そっちを見てもらってもいいです。
点群の表記法
それで、\(C\)とか\(D\)とか書いてあっても、訳がわからないので、まず表記法について話します。
点群の表記方は、シェーンフリース(Schoenflies)系とヘルマン-モーガン(Hermann-Mauguin)系の2種類があって、さっきのフローチャートは前者で書かれています。
この2つの対応はこちらの表のとおりです。
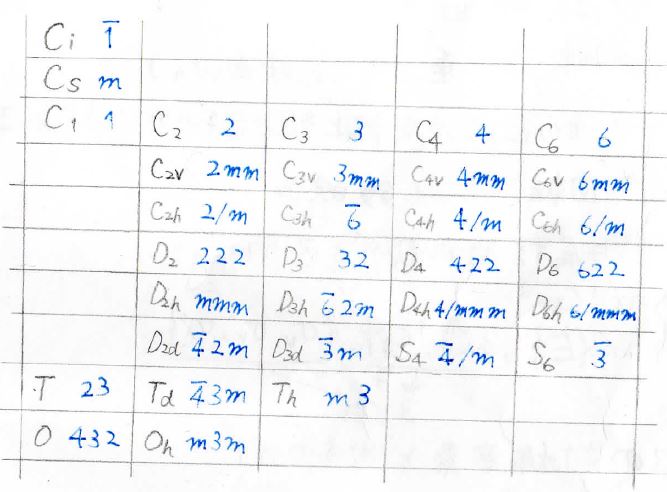
シェーンフリース系を黒、ヘルマン-モーガン系を青で示しています。
一般的に、今回のように分子1個の対称性を議論する際には黒のシェーンフリース系、たくさんの分子が並んでできる結晶の対称性を議論する際には青のヘルマン-モーガン系が使われます。
それで、シェーンフリース系の\(C\)や\(D\)という大文字と、\(\rm{h}\)や\(\rm{v}\)あるいは数字といった添字が意味するものを抽象的に示したのが、こちらの表です。
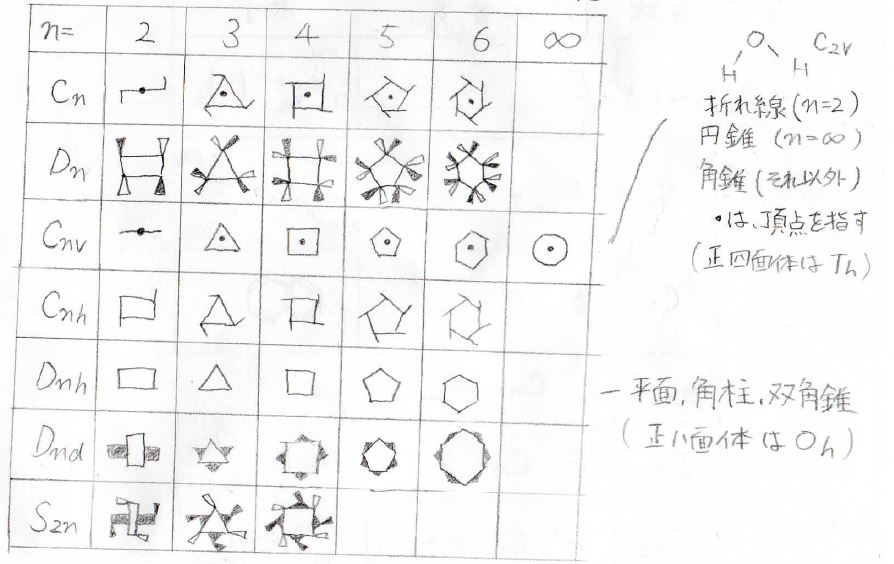
また、それぞれについて個別にお話しますので、それを見た後にここに戻ってきてもらえたらと思います。
ざっくりとしたイメージをいうと、数字が対称軸の次数に対応してるので、例えば\(3\)とついてたら、主軸方向から見たときに三角形になってるといった具合です。
あとは、その立体が正多面体なのかとか角錐なのか折れ線なのか直線なのかなどで、\(C\)とかDの分類が決まっています。
それでヘルマン-モーガン系の数字と文字の意味はこんな感じです。

数字は回転軸の次数、\(m\)は鏡映面があることを意味します。
\(/m\)は、その鏡映面が主軸に垂直なことを示します。
数字の上にバーがついているのは、その回転が反転と組み合わされていることを指します。
\(\bar{2}\)は鏡映要素を指すため、\(m\)となります。
そして、普通は\(m\)の前に数字が来ますが、その逆の表記をしているものがあって、これはその回転軸を含む鏡映面を持っていることを指します。
あと、\(mm\)のように表記されているものがあって、この\(m\)の文字数は鏡映面がいくつの類に分けられるかということを意味しています。
例えば、↓の対称操作についての記事で、練習問題としてアンモニア分子のすべての対称操作を考えました。

そのときに、\(2\)つの回転操作と\(3\)つの鏡映操作はまとめて類と呼ぶとお話しました。
同じ類に属する\(2\)つの対称操作は、その分子が持ついずれかの対称操作によって相似変換ができます。
もし、同じ類に属さない鏡映面があった場合には、\(mm\)となっていくわけです。
点群がもつ対称要素と分子例
はい、ここまで抽象的な話が続いて、わかりにくかったと思いますが、ここからはシェーンフリース系の表記で、それぞれの点群がもつ対称要素についてお話していきます。
また具体的に、どんな分子がその群に属するのか、その例も見ていきましょう。
\(C_1\)群、\(C_\rm{i}\)群、\(C_\rm{s}\)群
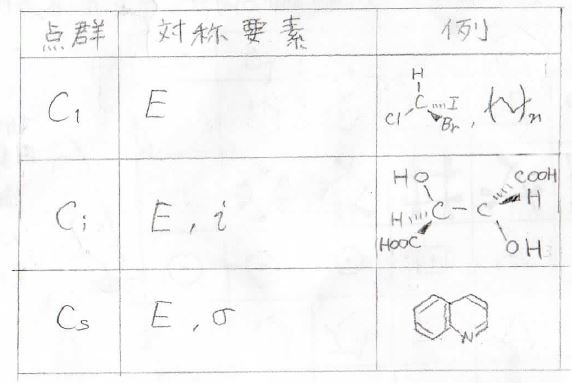
\(C_1\)群
まずは\(C_1\)群です。
これは、恒等操作以外の対称操作を持たない群で、最も対称性が低い分子が属します。
その例としては、不斉炭素を1つ持つキラルな分子、あとは高分子もそうです。
むちゃくちゃ硬くて短くない限り、対称操作を考えることは無理です。
\(C_\rm{i}\)群
続いての点群は\(C_\rm{i}\)群です。
恒等操作と反転操作のみが対称操作となる分子が属します。
その例は、メソ酒石酸です。
\(C_\rm{s}\)群
続いて、\(C_\rm{s}\)群です。
恒等操作と鏡映操作のみが可能な群です。
キノリンがその一例です。
\(C_n\)群、\(C_{n\rm{v}}\)群、\(C_{n\rm{h}}\)群

\(C_n\)群
続いて、\(C_n\)群です。
この群に属する分子は、\(n\)回回転軸を1つだけ持ちます。
例えば、トリフェニルホスフィンは\(C_2\)群に属します。
\(C_{n\rm{v}}\)群
そして次の\(C_{n\rm{v}}\)群では、さらにその主軸を含む鏡映面を\(n\)個持ちます。
アンモニアは\(C_{3\rm{v}}\)群に属します。
それで、塩化水素などの異核二原子分子はすべて、\(C_{\infty \rm{v}}\)群に属します。
回転軸は、2つの原子を結ぶ直線です。
\(C_{n\rm{h}}\)群
そして、今回紹介する最後の点群は、\(C_{n\rm{h}}\)群です。
主軸に対して垂直な鏡映面を持ちます。
例えば、トランス-1,2-ジクロロエチレンは、紙面に対して垂直な方向に\(2\)回回転軸を持ち、紙面と平行な鏡映面を持つので、\(C_{2\rm{h}}\)群に属します。
また、反転操作\(i\)は\(2\)回回転\(C_2\)と\(\sigma_\rm{h}\)の積であるため、\(C_{2\rm{h}}\)群では反転操作も対称操作になります。
ただし、点群の分類方法は、対称操作ではなく、あくまで対称要素で分類しているため、反転中心を持っているという書き方はしません。
\(D_n\)群、\(D_{n\rm{h}}\)群、\(D_{n\rm{d}}\)群
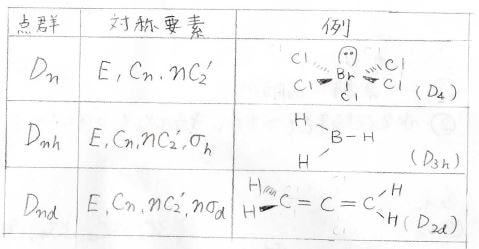
\(D_n\)群
次は、\(D_n\)群です。
これは、複数の回転軸を持つ群で、最も次数が大きい主軸と、それに垂直な\(n\)本の\(C_2\)軸があります。
五フッ化臭素などのように、同一平面上に同じものがあって、でもその平面に対しては非対称なものがこれにあたります。
\(D_{n\rm{h}}\)群
この平面に対しても対称なものは、次の\(D_{n\rm{h}}\)群になります。
ボランやベンゼンなど正多面体型の分子のほか、角柱型、そして一部例外はありますが、双角錐型の分子がこれに当たります。
また、水素や塩素などの同核二原子分子はすべて\(D_{\infty \rm{h}}\)群に属します。
\(D_{n\rm{d}}\)群
次の\(D_{n\rm{d}}\)群では、\(D_n\)群の要素に加えて、\(\sigma_\rm{d}\)面を\(n\)枚持ちます。
\(\sigma_\rm{d}\)面とは、主軸に垂直な隣り合う\(2\)本の\(C_2\)軸がなす角を二等分線するような鏡映面を指します。
主軸に垂直な\(\sigma_\rm{h}\)面は持っていません。
例えば、1,2-プロパジエン(アレン)は\(D_{n\rm{d}}\)群に属します。
\(S_n\)群
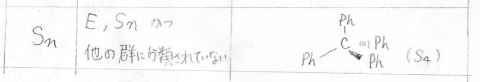
続いての点群は\(S_n\)群です。
これは回転軸、鏡映面、反転中心を持っておらず、回映軸だけ持っている群です。
特徴的なのが、他の群に分類されていないという条件です。
これは、\(2\)回回映操作が結局反転操作と同じになってしまうからです。
\(S_2\)群を考えようとしても、すでに\(C_\rm{i}\)群に分類されているので、\(S_2\)群を別に考えることはしませんよということです。
そして、\(S_n\)群に属する分子は、そのほとんどが\(S_4\)群に属していまして、例えばテトラフェニルメタンが該当します。
立方群
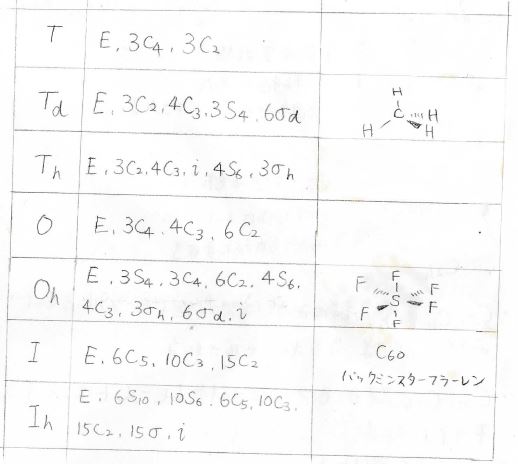
そして、ここからは立方群というものに入っていきます。
これらは主軸を複数本持っているという特徴があります。
\(T\)、\(O\)、\(I\)という大文字は、多面体の面の数を表しており、それぞれ四面体、八面体、二十面体に対応しています。
\(\rm{h}\)がついているのは、\(\sigma_\rm{h}\)面を持っていることを指し、\(\rm{d}\)がついている\(T_\rm{d}\)群は反転中心を持ちます。
添字がついていない\(T\)群、\(O\)群、\(I\)群は鏡映面も反転中心も持っていない立方群です。
それぞれの分子の例はこちらに示した通りです。
メタンは\(T_\rm{d}\)群、六フッ化硫黄は\(O_\rm{h}\)群に属します。
二十面体を書く画力はなかったので楽をしてますが、バックミンスター・フラーレンは\(I\)群に属します。
化合物の例で空欄になっているところは、今回自分が調べた限りでは見つけられなかったものです。
自分はもう自由に論文を読める環境におりませんので、誰かわかる方いらっしゃったらコメントで教えていただけますと、非常に助かります。
全回転群
そして、最後に紹介する点群は、全回転群です。
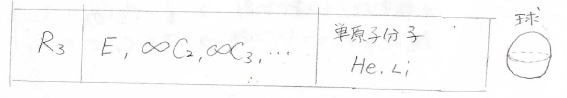
これは\(R_3\)群と表記し、全方向に対して任意の回転軸を何本でも考えることができます。
そんな立体は球しかありえず、球状の多原子分子はないので、原子だけが\(R_3\)群に属します。
点群からすぐにわかること
はい、点群の紹介は以上です。
ここからは点群からすぐにわかることについて、見ていきます。
永久双極子
まず、分子全体で永久電気双極子を持ちえない群があります。
それは、\(C_\rm{i}\)、\(C_n\)、\(C_{n\rm{h}}\)群以外のすべての群です。
例えば、\(C_{2\rm{v}}\)群に属する水分子は、酸素原子側が負、水素原子側が正に分極します。

分子全体でみたときには、主軸に垂直な方向についてキャンセルが起こるため、主軸と平行な双極子モーメントを持つことになります。
対して、\(C_{2\rm{h}}\)群に属するtrans-1,2-ジクロロエチレンでは、局所的な分極は起こっているものの、分子全体でみたときにはキャンセルされるので、永久双極子は持ちません。

ここで注意してもらいたいのは、\(C_\rm{i}\)、\(C_n\)、\(C_{n\rm{h}}\)群に属する分子であったとしても、絶対に永久双極子を持っているというわけではありません。
あくまで双極子を持ちうるという話です。
また、\(C_n\)、\(C_{n\rm{h}}\)群に属する分子が永久双極子を持っていた場合、その方向は必ず主軸と平行になります。
キラリティ
そして、点群がわかればキラリティの判別も可能です。
こっちはシンプルで、回映軸を持っていない群だけが、キラルになる可能性があります。
ただし、\(S_n\)群だけがアキラルになるわけではなくて、例えば反転操作は\(2\)回回映操作にあたるので、反転中心を持つ群もアキラルになります。
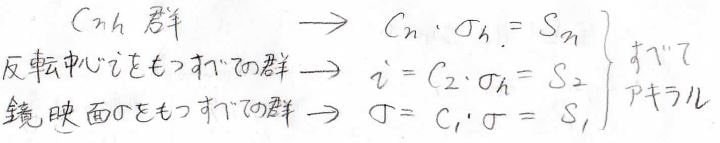
また、鏡映操作も\(1\)回回映操作と言えるため、鏡映面を持つ群もアキラルになります。
練習問題
それでは最後、練習問題をやってみましょう。
①これらの分子は、どの点群に分類されるでしょうか?
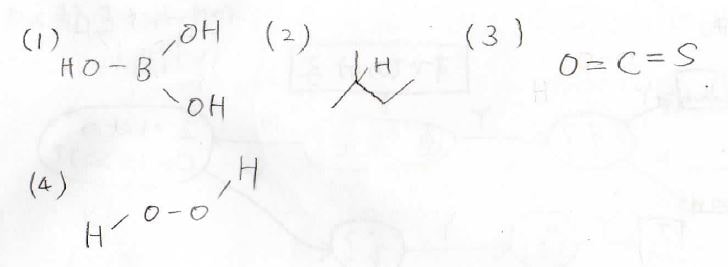
②これらの分子は、どの点群に分類されるでしょうか?
また、この中で永久双極子を持たない分子とアキラルな分子をすべて挙げてください。
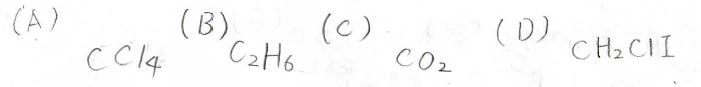
①
まず(1)のホウ酸は、\(3\)回回転軸があり、それに垂直な鏡映面も持ちます。
従って\(C_{3\rm{h}}\)群に属します。
続いて(2)の2-メチルブタンは、恒等操作以外の対称操作を持たないので\(C_1\)群に属します。
(3)の硫化カルボニルは、異核二原子分子同様に左右非対称な直線分子なので、\(C_{\infty \rm{v}}\)群となります。
(4)の過酸化水素は、\(2\)回回転軸を持ちますが、それ以外はないので\(C_2\)群です。
②
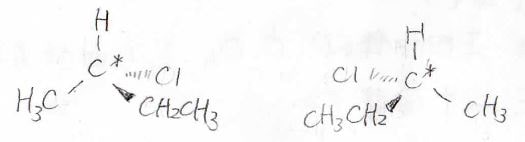
まず、Aの四塩化炭素は、正四面体型で、\(3\)本の\(C_2\)軸、\(S_4\)軸と\(4\)本の\(C_3\)軸、そして、\(6\)つの鏡映面を持ちます。
したがって、メタンと同じ\(T_\rm{d}\)群に属します。
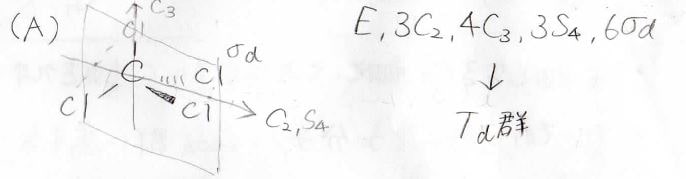
続いて、Bのエタンはちょっとややこしくて、配座によって対称性が変わります。
より安定である左のねじれ型配座は\(D_{3\rm{d}}\)群、右の重なり配座は\(D_{3\rm{h}}\)群です。

Cの二酸化炭素は左右対称な直線型分子なので、等核二原子分子同様に、\(D_{\infty \rm{v}}\)群に属します。
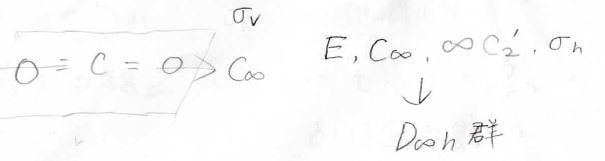
最後、Dのクロロヨードメタンは、鏡映面を1つ持つだけなので、\(C_\rm{s}\)群に属します。

そして、この中で永久双極子を持つのは、\(C_\rm{s}\)群に属するDのヨードクロロメタンだけです。
また、キラルな分子はありません。
ねじれ型配座のエタンは反転、それ以外は鏡映が対称操作になるため、いずれも回映軸を持っていることになります。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!



