こんにちは!
それでは今回も化学のお話やっていきます。
今日のテーマは、こちら!
動画はこちら↓
動画で使ったシートはこちら(reaction enthalpy)
それでは内容に入っていきます!
エンタルピーと熱量の関係
それではまず、エンタルピーと熱量の関係を軽く復習しておきましょう。
エンタルピーは内部エネルギー\(U\)に圧力\(p\)と体積\(V\)の積を足した量として定義されます。
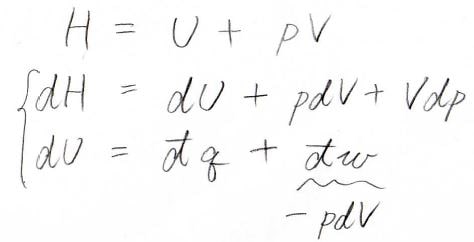
その微小変化量\(\rm{d}\)\(H\)は、全微分として\(\rm{d}\)\(U+p\rm{d}\)\(V+V\rm{d}\)\(p\)と表すことができます。
また、熱力学第一法則より、\(\rm{d}\)\(U\)は微小な熱量\(\rm{d’}\)\(q\)と微小な仕事\(\rm{d’}\)\(w\)の和であり、さらに\(\rm{d’}\)\(w=-p\rm{d}\)\(V\)となります。
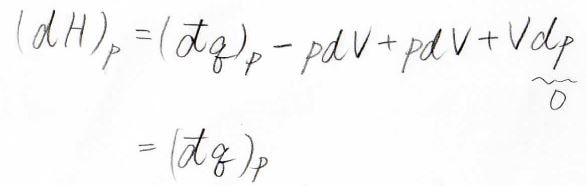
これらの式を組み合わせると、\(\rm{d}\)\(H=\rm{d’}\)\(q+V\rm{d}\)\(p\)となります。
化学で扱う反応の多くは、その前後で温度と圧力は変わらないとみなすことができるため、その場合は\(\rm{d}\)\(p=0\)から\(\rm{d}\)\(H=\rm{d’}\)\(q\)となります。
すなわち、エンタルピーの変化量は、圧力一定条件下において、反応に伴って吸収される熱量と一致します。
高校の化学で、反応が起こる際の熱量の収支を反応熱と言い、その符号から発熱反応と吸熱反応を判別しましたが、大学からは、エンタルピーの増減で判別することになります。
標準状態
続いて、標準状態というものを考えます。
理想気体のエンタルピーが温度に比例することからもわかるように、反応エンタルピーは温度に依存します。

また、一般的には圧力にも依存します。
そのため、ユニバーサルな値として、文献等に載せる場合には、ある温度と圧力に固定する必要があります。
そこで用いられるのが標準状態です。
圧力は\(1\ \rm{bar}\)、すなわち\(10^5\ \rm{Pa}\)で、温度には\(25^\circ \rm{C}\)がよく使われ、これは約束温度と呼ばれています。

しかし、常にこの値である必要はなく、明記してあれば他の値でも構いません。
例えば、ひと昔前だと標準圧力として\(1\ \rm{atm}\)、すなわち\(1.013×10^5\ \rm{Pa}\)が使われていました。
そして、標準状態におけるエンタルピー変化は、このような記号をつけて表します。
![]()
この記号はプリムソル記号と呼ばれ、標準であることを意味します。
( \(^\circ\) が同じ意味で、使われることもあります。)
元々は、貨物船に載せられる最大の積載量を海面の高さで表した満載喫水線というものに由来しています。
そして、この標準反応エンタルピーは、ユニバーサルな量にしたいので、\(\rm{mol}\)あたりの量として表します。
安定性の指標
ここからは実際に、標準状態における氷から水への融解を例に、反応エンタルピーを考えていきます。
縦軸をエンタルピー、横軸を反応座標としたポテンシャルカーブ※は下のようになり、固体から活性化障壁を超えて液体に変化します。
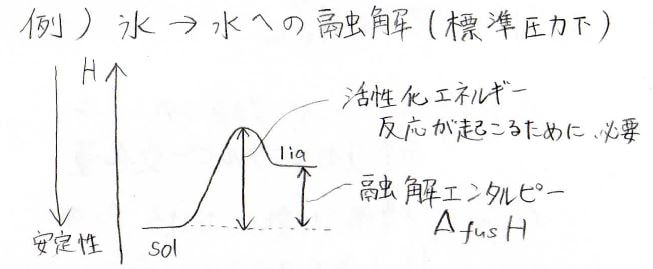
活性化障壁の頂点の状態は遷移状態と呼ばれ、変化が起こりやすい不安定な状態になります。
つまり、エンタルピーが大きいほど、変化が起こりやすいということなので、安定性は下向きに大きくなっていきます。
より厳密には、ポテンシャルカーブが上に凸(遷移状態)か下に凸(中間体)かという違いによって、系中に存在している時間に大きな差が生じます。
融解や蒸発などの状態変化に伴う反応エンタルピーは、そのときの温度を標準温度とすることが多いので、融点\(0\rm{^\circ C}\)を標準とすると、標準融解エンタルピーは\(+6.008\ \rm{kJ/mol}\)となります。

氷が溶けるときには、周りから熱を奪うので、この反応は吸熱反応になります。
このとき、反応前の氷は反応後の水より安定です。
反対に反応エンタルピーが負の値をとる場合は、発熱反応であり、生成物のほうが安定となります。
※アレニウスパラメータである活性化エネルギーと、反応系から遷移状態までのエンタルピー変化は一致しないため、本来、グラフの縦軸はポテンシャルエネルギーとするのが正しいです。
化学量数
それでは、もっと一般的にこんな反応式を考えていきましょう。

ここで、\(n\)は係数、\(\rm{A}\)は化学種です。
まず、化学量数\(\nu\)を下のように定義します。

言葉で説明すると、反応式の矢印より左側についてのみマイナスを付ける操作を行った係数が化学量数です。
(上記の「化学量論係数」は「化学量数」の誤りです。「化学量論係数」は、化学反応式の係数のことで、原系のものにマイナスを付けないものです。)
つまり、\(\nu_1=-n_1\)で、\(\nu_2=-n_2\)となります。
右側の生成系については、そのまま\(n=\nu\)となります。
そして、標準反応エンタルピーは、さっき定義した\(\nu\)を使って、下のように表されます。
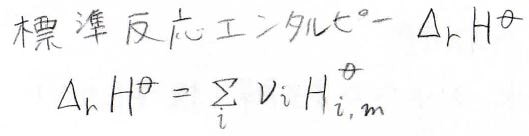
ここで注意してもらいたいのは、まず標準反応エンタルピーは、化学種\(\rm{A_i}\)の\(n_\rm{i}\ \rm{mol}\)あたりの量になります。

そして、\(H_{\rm{i, m}}\)は化学種\(\rm{A_i}\)の\(1\ \rm{mol}\)あたりの量です。
多くの場合、エンタルピーのゼロ点は絶対零度における値で考えますが、反応エンタルピーはあくまで変化量なので、違うところをゼロ点にして計算しても、同じ値になります。
練習問題
それでは最後、実際に標準反応エンタルピーを求めてみましょう。

右側の生成系は、そのままです。
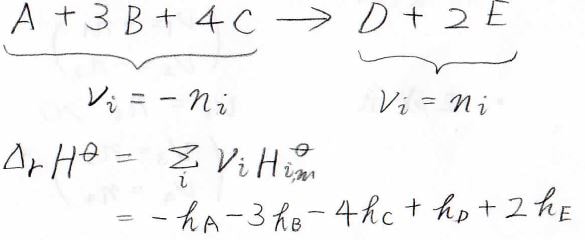
あとは、これに標準モルエンタルピーをかけて足し上げれば、標準反応エンタルピーは\(-h_\rm{A}\)\(-3h_\rm{B}\)\(-4h_\rm{C}\)\(+h_\rm{D}\)\(+2h_\rm{E}\)となります。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




