こんにちは!
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(group definition)
それでは内容にはいっていきます!
置換(線形代数学)で成り立つ積の演算
始めに、行列式の定義で出てきた置換というものを思い出してみましょう。
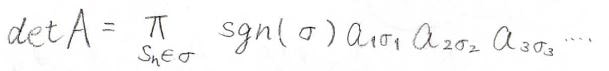
ここで\(\displaystyle \bf{\rm{A}}\)は行列、\(a_{i, j}\)は\(\bf{\rm{A}}\)の\((i, j)\)成分です。
\(\sigma\)が置換というもので、数の入れ替えを表します。
上の行に入れ替え前の順番、下の行に入れ替え後の順番を書きます。
詳しくは、こちらの記事でお話ししています。

\(S_n\)は、すべての\(n\)次置換の集合であり、例えば\(S_3\)に含まれる置換は、こちらに示したとおりになります。

順番を入れ替えないという置換もあって、これは恒等置換と呼びます。
そして、\(\sigma\)と\(\tau\)を置換としたとき、その積\(\sigma \tau\)はこのように考えることができます。
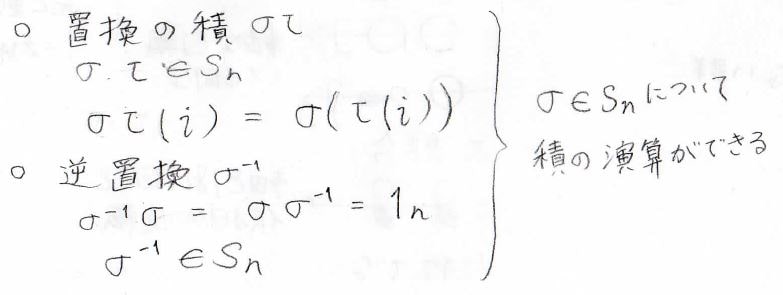
ここでは\(\sigma\)の入れ替えをしたあと、\(\tau\)の入れ替えをしています。
また、置換\(\sigma\)にかけることで恒等置換となる置換を考えることができます。
これを逆置換と呼び、\(\sigma^{-1}\)と表記します。
このとき、\(\sigma^{-1}\)は一意的に決まり、\(\sigma \sigma^{-1}=\sigma^{-1}\sigma\)という交換もできます。
以上のように、集合\(S_n\)に含まれる置換同士だと、積の演算ができるという特徴があります。
剰余類で成り立つ和の演算
一方で、その集合の中で積を考えることができないものもあります。
その1つが剰余類です。
まず、小学校で習う余りのある割り算を考えます。

\(a\)、\(n\)、\(r\)を自然数、\(q\)を整数として\(a=qn+r\)が成り立ち、また先ほどとは異なる自然数\(a’\)、\(r’\)と整数\(q’\)についても\(a’=q’n+r’\)が成り立つとします。
ここで2つの余りの値\(r\)と\(r’\)が同じとき、下のように表記し、「\(n\)を法として\(a\)と\(a’\)は合同である」と言います。
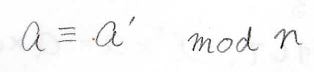
そして、\(n\)で割ったときに余りが\(a\)となる整数の集合を\([a]\)と表すことにします。
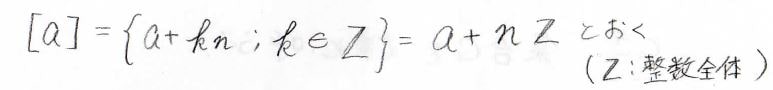
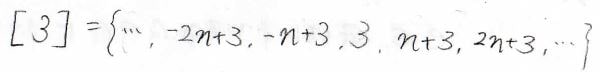
例えば、\([3]\)は\(3\)や\(n+3\)、\(2n+3\)、それに\(-n+3\)、\(-2n+3\)を含む集合になります。
この\([a]\)のことを剰余類と呼びます。
さらに、剰余類同士の足し算\([a]+[b]\)を\([a+b]\)と定義すると、足し算の結合法則や交換法則を満たすことが確認できます。
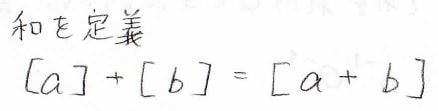
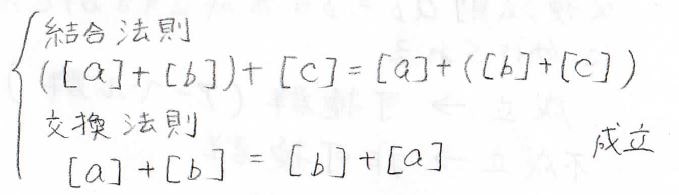
また、余りが\(0\)になる剰余類も\([0]\)と考えることができ、下のようにに負の剰余類\([-a]\)も考えることができます。

群の定義
そして、置換の積の演算が成り立つ状況や剰余類の和の演算が成り立つ状況を統一的に扱うため、Cayleyによって群というものが定義されました。
こちらがその定義で、まず集合\(G\)に含まれる\(a\)と\(b\)について、その積\(ab\)を考えることができ、また\(ab\)も集合\(G\)に含まれます。

そして、\(a(bc)=(ab)c\)という結合法則も成り立ちます。
また、集合\(G\)に含まれるすべての元に対して、積をとっても同じ元のままになる単位元も集合\(G\)に含まれます。
最後、集合に含まれるそれぞれの元に対して、積をとって単位元となるような逆元が存在し、これも集合\(G\)に含まれるとき、集合\(G\)のことを群と呼びます。
回りくどいですが、ここで言っていることはさっき置換について確認したことです。
群の性質
群に含まれる元について、その性質を一部紹介すると、まず、すべての元に対して、単位元は一意的に決まります。
逆元は、それぞれの元に対して、一意的に決まります。

そして、\(ab\)の逆元は\(b^{-1}a^{-1}\)になります。
\(ab=ba\)という積の交換法則は、すべての群で成り立つわけではなく、成り立つ群は可換群もしくはアーベル群、成り立たない群は非可換群と呼ばれます。
ちなみに、置換は非可換群に該当します。
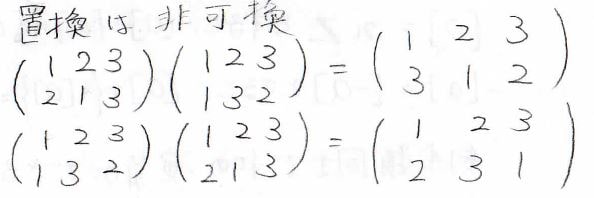
群論と化学
最後に、なぜ化学で群の考え方が必要になってくるのかを、ざっくりと説明します。
思い出してほしいのは、分子軌道法です。
水素分子を例にしますが、電子は2つの陽子のそれぞれと静電的相互作用をしていて、全体の波動関数\(\varphi\)は\(C_\rm{A} \phi_\rm{A}+C_\rm{B} \phi_\rm{B}\)と書かれます。
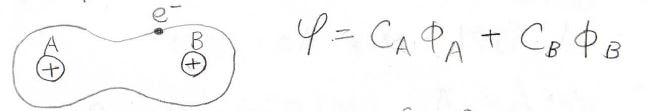
ここで\(\rm{A}\)と\(\rm{B}\)は、2つの原子核に対応し、\(\phi\)は原子の波動関数、\(C\)は変分法に使う未知定数です。
詳しくは、こちらを参照してください。

結果だけを示すと、水素分子中の電子のエネルギーは2つの解を持ち、複号同順で\(\displaystyle \frac{\alpha \pm \beta}{1 \pm S}\)となります。
ここで、\(\alpha\)、\(\beta\)、\(S\)はそれぞれクーロン積分、共鳴積分、重なり積分と呼ばれ、このような式で表されます。
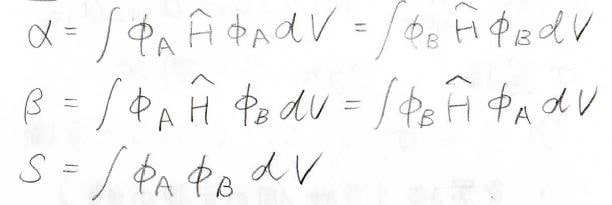
ここで\(\hat{H}\)は、ハミルトニアンです。
水素原子と水素分子のエネルギーを図にするとこのようになり、低いエネルギー側である結合性軌道に電子が入ることで安定な分子になります。
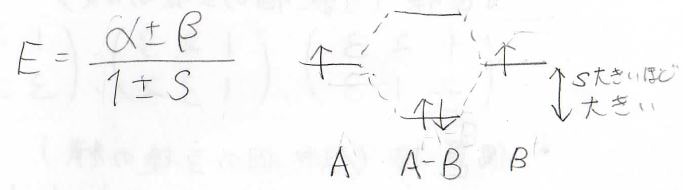
ここで重要なのが重なり積分\(S\)で、\(S\)は(1\)に近い値であるほど、原子から分子になったときのエネルギー差が大きくなり、より安定な結合を形成することができます。
\(S\)は、2つの原子軌道がどれだけ重なっているかを表すため、結合を作る2原子の距離が短いほど大きくなります。
そして、もう1つ\(S\)に影響するのが、軌道の対称性です。
例えば、\(x\)軸方向へ向いている\(p_x\)軌道と\(y\)軸方向へ向いている\(p_y\)軌道の組み合わせでは、軌道の重なりがないため、\(S=0\)となります。

このような関係は、直交していると言います。
それに対して、\(\displaystyle \sigma\)結合では、2つの原子を結ぶ軸をどれだけ回しても、回す前とまったく同じ形になります。
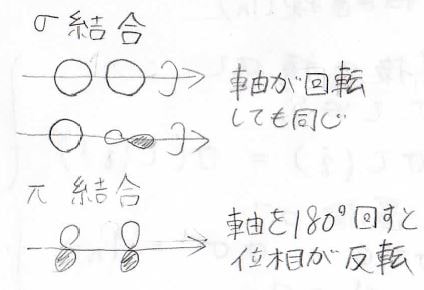
元の形と重なるような動かし方のことは対称操作と呼ばれます。
対称操作については、こちらを参照してください。

そして、\(\displaystyle \pi\)結合では、2つの原子を結ぶ軸を\(180^\circ\)回したときに位相が反転します。
同じ対称性をもつ軌道どうしでは、原子間距離がとても長い場合を除き、重なり積分は\(\displaystyle 0\)ではない値をとります。
詳しくは、こちらで説明しています。

そのため、対称性は軌道同士、あるいは分子同士の相互作用を考えるのに大切な要素になっています。
ある分子に対して、可能なすべての対称操作を群として分類すると、相互作用がわかりやすくなるということで、化学に群論が使われています。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




