こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(relation between partition function and equilibrium constant)
それでは内容に入っていきます!
ギブズエネルギーの統計学的表現
始めに、集合分配関数を使って、熱力学量がどのように表せたのかをおさらいします。
詳しい導出の過程は、こちらの記事を参照してください。

前回、エントロピーと分子運動の関係について考えたときに、エントロピーと集合分配関数の関係を利用しました。
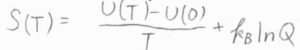
ヘルムホルツエネルギーの定義\(U-TS\)の\(S\)にその式をあてはめると、絶対温度\(T\)におけるヘルムホルツエネルギー\(A(T)=A(0)-k_\rm{B}\)\(T\ln{Q}\)となります。
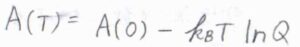
ここで、\(U\)は内部エネルギー、\(S\)はエントロピー、\(k_\rm{B}\)はボルツマン定数、\(Q\)は集合分配関数(正準分配関数)です。
\(A(0)\)は、絶対零度におけるヘルムホルツエネルギーです。
さらに、熱力学基本式より、ヘルムホルツエネルギーの完全微分\(\rm{d}\)\(A\)は、\(-S\rm{d}\)\(T-p\rm{d}\)\(V\)で与えられるので、\(\displaystyle p=-(\frac{\partial A}{\partial V})_T\)と書けます。
ここで、\(p\)は圧力、\(V\)は体積です。
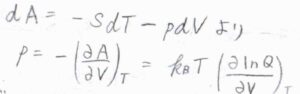
\(A(T)=A(0)-k_BT\ln{Q}\)を圧力の式に代入すると、\(p=k_\rm{B}\)\(\displaystyle T(\frac{\partial \ln{Q}}{\partial V})_T\)となり、\(A+pV\)で定義されるギブズエネルギー\(G\)も分配関数を使って表せることになります。
絶対温度\(T\)におけるギブズエネルギー\(G(T)\)は、\(G(0)-k_\rm{B}\)\(T\ln{Q}+k_\rm{B}\)\(\displaystyle TV(\frac{\partial \ln{Q}}{\partial V})_T\)で与えられます。
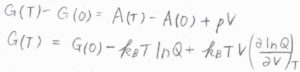
分子分配関数とギブズエネルギーの関係
ここからは、理想気体の系について考えていきます。
理想気体の状態方程式\(pV=nRT\)が成り立つとき、\(G=A+nRT\)であり、\(G(T)=G(0)-k_BT\ln{Q}+nRT\)と書けます。
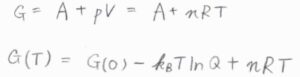
さらに、分子が区別できない場合について、分子分配関数を使ってギブズエネルギーを表すことを考えます。
分子数を\(N\)として、分子分配関数\(q\)と集合分配関数\(Q\)の関係は、\(\displaystyle Q=\frac{q^N}{N!}\)で与えられます。
大きな自然数の階乗について、スターリングの近似式を利用すると、\(\ln{Q}\approx N\ln{q}-N\ln{N}+N\)と近似できます。

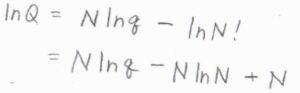
これを\(G(T)\)の式に代入すると、\(G(T)=G(0)-Nk_\rm{B}\)\(\displaystyle T\ln{(\frac{q}{N})}\)という関係が得られます。
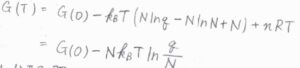
真数である\(\displaystyle \frac{q}{N}\)は、1分子あたりの熱的に励起可能な状態の数の平均値を意味します。
これをモルあたりの平均値にしたもの、すなわち\(\displaystyle \frac{q}{n}\)をモル分配関数\(q_\rm{m}\)と定義すると、平衡定数などを考えるのに便利な形になります。
アボガドロ数を\(N_\rm{A}\)と表すと、\(\displaystyle G(T)=G(0)-nRT\ln{(\frac{q_\rm{m}}{N_\rm{A}})}\)と書けます。
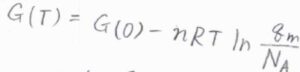
モル分配関数と平衡定数の関係
ここから、本題である分配関数と平衡定数の関係を考えていきます。
ある化学反応\(\displaystyle \sum_\rm{J}\)\(\nu_\rm{J}J=0\)についての平衡定数\(K\)と標準反応ギブズエネルギー\(\Delta_\rm{r}\)\( G^\circ\)の関係は、\(\Delta_\rm{r}\)\( G^\circ=-RT\ln{K}\)で与えられます。
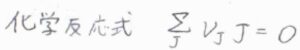
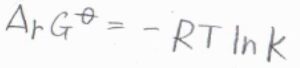
ここで、\(\nu_\rm{J}\)は化学量数、\(\rm{J}\)は化学種です。
標準反応ギブズエネルギー\(\Delta_\rm{r}\)\( G^\circ\)は、それぞれの化学種の標準化学ポテンシャル、すなわち純粋なときの標準モルギブズエネルギーを使って表すことができるため、先ほどのモル分配関数を用いた式を代入します。
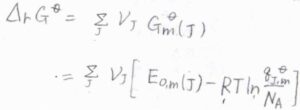
ここで、絶対零度におけるモルギブズエネルギー\(G_\rm{m}\)\((0)\)をモルあたりの零点エネルギー\(E_\rm{0, m}\)\((J)\)と書き換えています。
さらに、化学反応による零点エネルギー変化\(\Delta_\rm{r}\)\( E_0\)とすると、\(\Delta_\rm{r}\)\(\displaystyle G^\circ=-RT[-\frac{\Delta_\rm{r}\mathit{E}_0}{RT}+\ln{\{\prod_\rm{J}(\frac{\mathit{q}_{J, m} ^\circ}{\mathit{N}_{A}})^{\nu_{J}}}\}]\)と書けます。
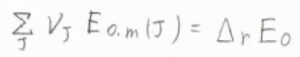
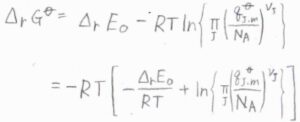
ここで、\(\displaystyle \prod\)は積を表します。
\(\Delta_\rm{r}\)\( G^\circ=-RT\ln{K}\)と照らし合わせると、上の式の右辺が\(-RT\ln{K}\)と等しいことになります。
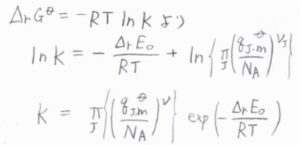
したがって、\(\displaystyle \ln{K}=-\frac{\Delta_\rm{r}\mathit{E}_0}{RT}+\ln{[\prod_\rm{J}(\frac{\mathit{q}_{J, m} ^\circ}{\mathit{N}_A)^{\nu_J}}]}\)となります。
対数を外すと、\(\displaystyle K=\prod_\rm{J}\)\(\displaystyle (\frac{q_\rm{J, m}^\circ}{N_\rm{A}})^{\nu_\rm{J}}\)\(\displaystyle \exp{(-\frac{\Delta_\rm{r} \mathit{E}_0}{RT})}\)と書けます。
これが、それぞれの化学種のモル分配関数と平衡定数の一般的な関係です。
解離平衡の例
このままだと、複雑な式でわかりにくいので、解離平衡を例に具体的に考えてみましょう。
二原子分子\(\rm{X}_2\)が解離して、2つの単原子分子\(\rm{X}\)になるという反応を順反応として、逆反応も起こることを考えます。

\(\rm{X}_2\)と\(\rm{X}\)は、いずれも理想気体です。
それぞれの分圧を\(p_\rm{X_2}\)、\(p_\rm{X}\)としたとき、平衡定数\(K\)は、\(\displaystyle \frac{p_\rm{X}^2}{p_\rm{X_2}\mathit{p}^\circ}\)で与えられます。
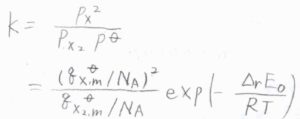
ここで、\(p^\circ\)は標準圧力です。
先ほどのモル分配関数を使った形で書くと、\(\displaystyle \frac{(q_\rm{X, m}^\circ)^2}{q_\rm{X_2, m}^\circ \mathit{N}_\rm{A}}\exp{(-\frac{\Delta_\rm{r} \mathit{E}_0}{RT})}\)となります。
\(\Delta_\rm{r}\)\( E_0\)は、モルあたりの結合エネルギーであり、\(N_\rm{A}\)\(hc\tilde{D}(\rm{X-X}\)\()\)と書けます。
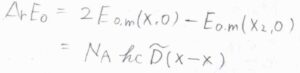
ここで、\(\tilde{D}(\rm{X-X}\)\()\)は波数で表した結合エネルギー、\(h\)はプランク定数、\(c\)は光の速さです。
実験的には、モル分配関数を分光学的データから算出するために、並進や回転、振動運動の寄与に分けて考える必要があります。
まず、単原子分子のモル分配関数である\(q_\rm{X, m}\)\(^\circ\)は、回転運動と振動運動を考えなくてもよいので、絶対零度近傍を除けば、\(\displaystyle \frac{g_\rm{X, 0}^\rm{E}\mathit{V}_\rm{m}^\circ}{\Lambda_\rm{X}^3}\)と表すことができます。
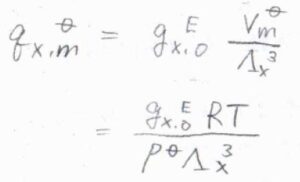
ここで、\(g_\rm{X, 0}\)\(^\rm{E}\)は基底電子状態の縮退度、\(V_\rm{m}\)\(^\circ\)は標準圧力におけるモル体積、\(\Lambda_\rm{X}\)は熱波長(または熱的ド・ブロイ波長)です。
理想気体の状態方程式より\(V_\rm{m}\)\(\displaystyle ^\circ=\frac{RT}{p^\circ}\)であるため、\(q_\rm{X, m}\)\(\displaystyle ^\circ=\frac{g_\rm{X, 0}^\rm{E}\mathit{RT}}{p^\circ \Lambda_\rm{X}^3}\)とも書けます。
一方、二原子分子である\(\rm{X}_2\)については、回転と振動も考慮する必要がありますが、ここではそれぞれの分子分配関数への寄与を\(q_\rm{X}\)\(_2^\rm{R}\)、\(q_\rm{X}\)\(_2^\rm{V}\)と表すことにします。
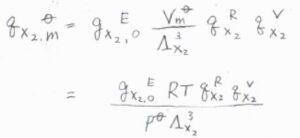
すると、\(\rm{X}_2\)についてのモル分配関数\(q_\rm{X_2, m}^\circ\)は、\(\displaystyle \frac{g_\rm{X_2, 0}^\rm{E}\mathit{RTq}_\rm{X_2}^\rm{R}\mathit{q}_\rm{X_2}^\rm{V}}{p^\circ \Lambda_\rm{X_2}^3}\)と表されます。
最後に、以上の結果を平衡定数の式に代入して整理すると、\(\displaystyle K=\frac{(g_\rm{X, 0}^\rm{E})^2\mathit{k}_\rm{B}\mathit{T}\Lambda_\rm{X_2}^3}{g_\rm{X_2, 0}^\rm{E}\mathit{p}^\circ \mathit{q}_\rm{X_2}^\rm{R}\mathit{q}_\rm{X_2}^\rm{V}\Lambda_\rm{X}^6}\exp{[-\frac{hc\tilde{D}(\rm{X-X})}{k_\rm{B}\mathit{T}}]}\)となります。
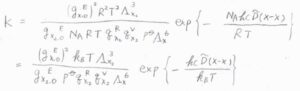
温度と分子の質量から熱波長を計算し、分光法から回転と振動の分配関数、分光法や熱量測定から結合エネルギーがわかれば、平衡定数も計算することができます。
この式の中には、遷移状態の情報は含まれておらず、平衡定数の算出に反応速度定数を使うことはありません。
反応機構が未知の反応についても、適用することができます。
分子論的解釈
最後に、平衡定数の物理的な意味を分子論的に考えて終わります。
ここでは、なるべく単純に視覚化するために、1分子から1分子への反応を例に考えます。
反応系の化学種を\(\rm{R}\)、生成系の化学種を\(\rm{P}\)とします。
こちらの図では、\(\rm{P}\)よりも\(\rm{R}\)の方が基底状態のエネルギーは低く、エネルギー準位の間隔はとても大きくなっています。
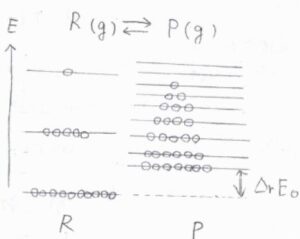

熱力学的な安定性だけを考えれば、より安定な\(\rm{R}\)に反応物側へと傾くため、平衡定数は\(1\)よりも小さくなると予想されます。
ただ、励起可能な状態の数にあまりにも大きな差がある場合は、\(\rm{P}\)が多く存在することになる可能性があります。
高温であるとして近似すれば、\(\rm{P}\)の分子分配関数\(q_\rm{P}\)と\(\rm{R}\)の分子分配関数\(q_\rm{R}\)の関係が\(q_\rm{P}\)\(\displaystyle \gt \frac{q_\rm{R}}{1-\Delta_\rm{r} \mathit{E}_0/\mathit{RT}}\)となるとき、吸熱反応が起こる方向へと平衡が傾くと考えられます。
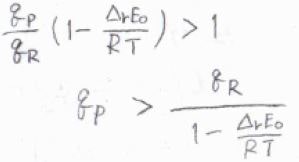
ただ、絶対零度近傍では、励起可能な状態の数が基底状態の縮退度とほとんど等しくなるため、熱力学的な安定な方向、すなわち発熱反応が起こる方向へと平衡が傾きます。
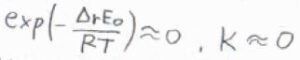
低温でなくとも、反応物と生成物でエネルギー準位の間隔が同じくらいのときには、熱力学的に安定な方向へ傾くことになります。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




