こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(Van der Waals)
それでは内容に入っていきます!
理想気体の状態方程式
始めに、理想気体の状態方程式について、少しだけお話しします。
まず、理想気体と似た言葉に完全気体という言葉があるのですが、これを区別することはあまり多くありません。
厳密には、理想気体は分子間相互作用がすべて同じ大きさのものを指し、完全気体はさらにその相互作用がすべて\(\displaystyle 0\)のものを指します。
理想気体と一般に呼ばれているものは、厳密には完全気体になるのですが、あまり気にしないことが多いです。
当サイトにおいても、理想気体の方を使いますが、厳密には完全気体のことであることを言っておきます。
その理想気体の状態方程式は、ボイルの法則、シャルルの法則、アボガドロの法則から導かれ\(pV=nRT\)となります。

\(p\)が圧力、\(V\)が体積、\(n\)が物質量、\(R\)が気体定数、\(T\)が絶対温度です。
この式を補正して実在気体を表そうというのが、今回のテーマです。
理想気体では無視される要素
それでは、どういう補正をしたらよいのでしょうか?
理想気体では無視されている重要な要素は、2つあります。
その1つ目は、分子の大きさです。
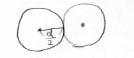
理想気体では、分子は質点として存在していますが、実際には、分子は必ず体積をもちます。
その結果、分子の中心同士の間には近づける限界があり、その距離は分子の直径\(d\)になります。
分子の中心が存在しえない領域の体積のことを排除体積と言います。
分子が\(N\)個あるときには、全体の排除体積はこの式で求められます。
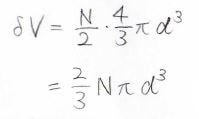
\(2\)で割るのは、2つの分子間で排除体積を考えているからです。
そして、もう1つ実在気体の非理想性に関係するのが、分子間相互作用です。
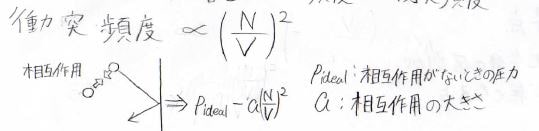
上の図のように、分子間で仮に引力が生じたとすると壁に衝突したときに、壁に与える力積の大きさが相互作用のないときよりも少し小さくなります。
この相互作用が起こる確率は、つまり2つの分子が十分に近づく確率と考えることができ、それは2分子の衝突確率に比例します。
分子の衝突確率は、体積\(V\)の空間中の同じ位置に2つの分子の中心が存在する確率になります。
1つの分子中心がある決まった位置にいる確率は分子数\(N\)に比例し、また体積\(V\)に反比例します。
2分子については、これが二重に起こる確率を考えるので、\(\displaystyle (\frac{N}{V})^2\)に比例します。
ここで、比例定数の\(a\)は相互作用の大きさを表すパラメータであり、物質定数となります。
以上、分子の排除体積と分子間相互作用を考慮すると、圧力は下の式で書けます。

ここで、\(b\)は\(1\ \rm{mol}\)あたりの排除体積です。
\(V-nb\)は分子の中心が存在できる空間の体積になります。
また、示量性である体積を示強性のモル体積\(V_\rm{m}\)に書き換えることもできます。
そして、この式の両辺に\(V_\rm{m}-b\)をかけて整理すると、下の式が出てきます。
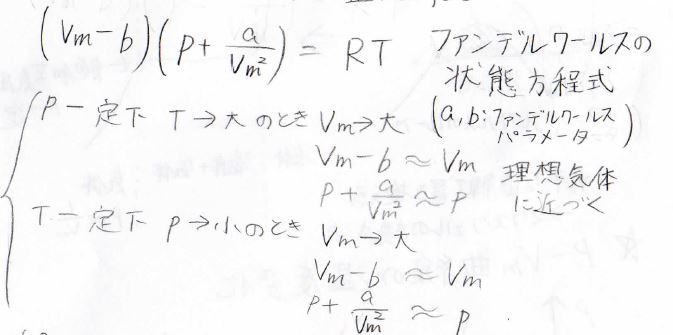
この式が、実在気体のための補正を加えた状態方程式で、ファンデルワールスの状態方程式と呼ばれます。
そして、補正のための定数\(a\)と\(b\)は、ファンデルワールスパラメータと言います。
この式からわかることとして、まず圧力一定にして温度を上げた場合には\(V_\rm{m}\)が大きくなり、\(b\)を無視できるようになります。
したがって、温度を上げると実在気体は理想気体に近い挙動になります。
同様に、温度を一定にして圧力を小さくした場合にも\(V_\rm{m}\)は大きくなるため、高温もしくは低圧条件下で理想気体に近いふるまいを見ることができることになります。
圧力とモル体積の関係
続いて、圧力\(p\)とモル体積\(V_\rm{m}\)の関係について、調べてみましょう。
関数の概形を調べるために偏微分すると、下記の上側の式になります。
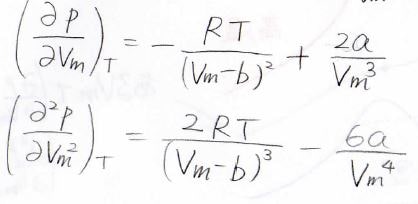
もう一度偏微分すると、下側の式のようになります。
ここで、二階の偏微分を考えると、第一項が正、第二項が負になるため、温度によっては圧力が変曲点をもつことになります。
そして、そのときの\(p\)-\(V_\rm{m}\)グラフは、下のような概形になります。
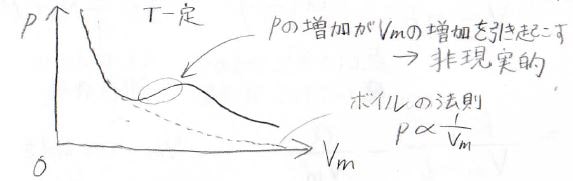
ここで、点線は理想気体のボイルの法則からくるものです。
ここで、注目すべきは傾きが正になって、体積が大きくなるほど圧力が上がるという非現実的な変化が予想されるということです。
この上下の振動のことは、ファンデルワールスのループと呼び、本来物質量が一定でこのようなことは起こりえないので、現実的には次のような操作をします。
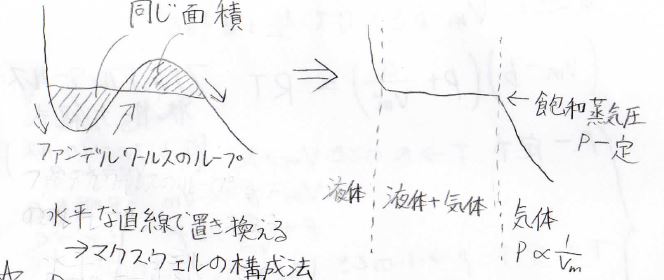
まず、2つの領域の面積が等しくなるよう水平線を引きます。
そして、非現実的な挙動にならないように、グラフの曲線の一部を水平線に置き換えます。
すると、水平線の領域で圧力は体積に依存しないことになります。
こうすることにより、液相と気相の共存状態を表します。
その圧力が飽和蒸気圧ということになります。
これより体積が小さい領域は液体のみ、体積が大きい領域は気体のみの状態に対応します。
この水平線による置き換えは、マクスウェルの構成法と言います。
また、液相と気相の共存領域も温度によっては見えないことがあります。
そもそも液体と気体は、流体という同じ分類に入るのですが、分子間距離に明確な違いがあるため、普段は明確に区別できています。
しかし、とても温度が高い場合には分子が大きな運動性をもつため、液体の分子間距離が長くなり、やがて気体の分子間距離と等しくなったところで、液体と気体の区別がなくなります。
\(p\)-\(V_\rm{m}\)グラフで温度変化を考えたのが下の図です。
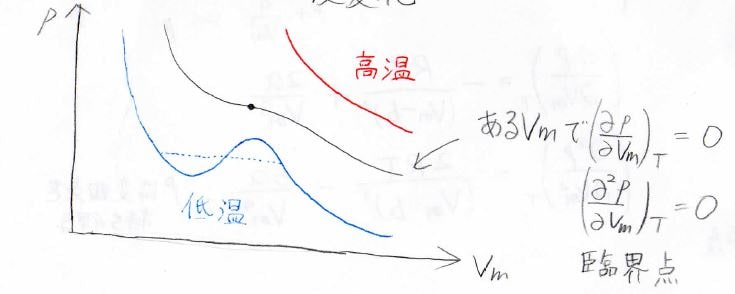
赤が高温、青が低温です。
高温では、ボイルの法則で圧力は体積に反比例し、低温では液相と気相の二相領域が存在します。
そして、ちょうど液体と気体の分子間距離が同じになり区別できなくなる温度での黒色の曲線で、一階と二階の偏導関数がどちらも\(0\)になる\(V_\rm{m}\)の値が存在します。
ここでは二相領域が点として存在していて、液体と気体が連続的に変わるようなイメージです。
この点は臨界点と呼ばれ、そのときの温度を臨界温度、そのときのモル体積を臨界モル体積、圧力を臨界圧力と呼びます。
これらのパラメータについては、こちらを参照してください。

まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!