こんにちは！
それでは今日も化学のお話やっていきます。
今回のテーマはこちら！
動画はこちら↓
動画で使ったシートはこちら(vibration rotation spectrum)
それでは内容に入っていきます！
赤外分光法
スペクトルの概形
まず、塩化水素ガスのFT-IR測定で得られるスペクトルの概形を示します。
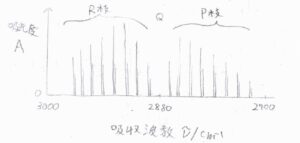
横軸が吸収波数で、縦軸が吸光度です。
二原子分子なので、振動モードは1つだけになるはずですが、実際には\(10\ \rm{cm}\)\(^{-1}\)という狭い間隔でほぼ等間隔に並んだ複数本のピークが観測されます。
これは、振動遷移と同時に回転遷移を起こっていることを示しています。
\(2880\ \rm{cm}\)\(^{-1}\)くらいに純粋な振動遷移の吸収ピークがあるはずですが、そこにはピークが観測されないため、回転遷移なしに塩化水素の振動遷移は起こらないということがいえます。
二原子分子の振動スペクトルについては、こちらも参照してください。
回転遷移の個別選択律は、純回転遷移と同じく、回転量子数\(J\)の変化\(\Delta J= \pm 1\)であり、\(\Delta J=0\)の遷移は禁制となります。
ただし、一酸化窒素など一部の例外では、\(\Delta J=0\)のピークが観測されます。
一酸化窒素はオクテット則を満たさず、\(\pi\)軌道に電子が1つだけあることで常磁性になる分子であり、二原子分子でありながら、主軸まわりの回転についても角運動量をもつためです。
吸収波数
複数のピークは3つに分類されます。
まず、\(\Delta J=0\)のピークをQ枝(Qブランチ)といいます。
\(\Delta J=-1\)のピークをP枝(Pブランチ)、\(\Delta J=+1\)のピークをR枝(Rブランチ)といいます。
もう一度グラフを見ると、こういう形になります。
それでは、それぞれのピークの吸収波数がどのように書けるのかを考えていきましょう。
振動エネルギーと回転エネルギーの和を波数単位で表したものを\(\tilde{S}(v, J)\)とします。
すると、\(\tilde{S}(v, J)=(v+1/2)\tilde{\nu}+\tilde{B}J(J+1)\)と書けます。
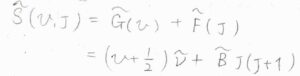
ここで、\(\tilde{\nu}\)は波数単位で表した振動準位間のエネルギー、\(\tilde{B}\)は回転定数です。
振動と回転のエネルギー準位については、こちらを参照してください。
Q枝の吸収波数\(\tilde{\nu}_\rm{Q}\)\((J)\)は、単純な振動準位間の差であるため、\(\tilde{\nu}\)となります。
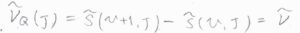
P枝の吸収波数\(\tilde{\nu}_\rm{P}\)\((J)\)は、回転状態が緩和した分だけ小さくなるため、\(\tilde{\nu}-2\tilde{B}J\)となります。
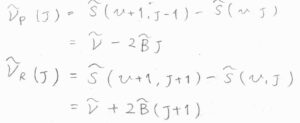
R枝の吸収波数\(\tilde{\nu}_\rm{R}\)\((J)\)は、回転状態の励起に使われた分だけ大きくため、\(\tilde{\nu}+2\tilde{B}(J+1)\)となります。
組み合わせ差
ただ、実際には回転定数\(\tilde{B}\)が振動状態に依存するということが起こります。
いま、振動量子数\(v\)のときの回転定数を\(\tilde{B}_v\)としておきます。
回転定数が振動状態に依存する原因としては、まずポテンシャルの非調和性があります。
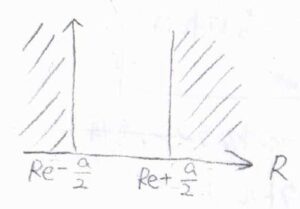
平衡核間距離\(R_\rm{e}\)\(\)が変化することで、慣性モーメントも変化します。
また、調和ポテンシャルで平衡核間距離が一定であったとしても、振幅が大きくなることにより、\(1/R^2\)の平均値は変化するので、慣性モーメントが変化することになります。
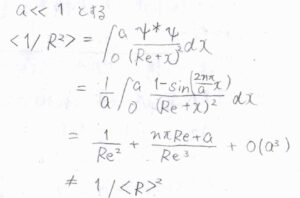
\(\tilde{B}_v\)を用いて、振動量子数\(v\)から\(v+1\)への遷移について、P、Q、R枝の吸収波数を書くと、こちらのようになります。
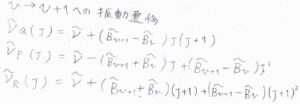
これにより、仮にQ枝が観測されていたときには、ピークが小さく分裂するということになります。
遷移前と遷移後のいずれかが一致する2つの吸収波数の差をとると、2つの回転定数のうちの片方を消去することができます。
これを組み合わせ差といいます。
たとえば、\(\tilde{\nu}_\rm{R}\)\((J-1)-\tilde{\nu}_\rm{P}\)\((J+1)=2(2v+1)\tilde{B}_v\)となるので、実験的に\(\tilde{B}_v\)を求めることができます。
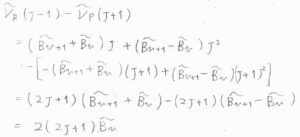
ラマン分光法
ここからは、ラマン散乱をともなって振動と回転の遷移が起こった場合について、考えていきます。
選択律
振動ラマンスペクトルの選択概律は、分子の振動により分極率に変化が生じなければならないというものです。
二原子分子の場合は、同核、異核に関わらず、結合の伸縮により分極率が変化するため、振動ラマン活性になります。
個別選択律は、振動量子数変化\(\Delta v\)が\(+1\)か\(-1\)の遷移だけが許容されるというものです。
さらに気相のスペクトルでは、同時に回転遷移が起こることで波長の異なるいくつかの散乱光が得られます。
このとき、回転量子数変化は\(0\)、\(+2\)、\(-2\)のいずれかとなります。
ここでは、一次元調和振動子を例に個別選択律の根拠を考えます。
\(x\)を平行核間距離\(R_e\)からの変位とし、入射光の電場を\(\boldsymbol{E}(t)\)、核間距離に依存する分子の誘電率を\(\alpha(x)\)とすると、入射光によって生じる誘起双極子モーメント\(\hat{\boldsymbol{\mu}}\)は、\(\alpha(x)\boldsymbol{E}(t)\)となります。
状態\(\rm{i}\)\(\)から\(\rm{f}\)\(\)への遷移について、遷移双極子モーメント\(\boldsymbol{\mu}_\rm{fi}\)\(\)は\(\int \psi_\rm{f}\)\(^\ast \hat{\boldsymbol{\mu}} \psi_\rm{i}\)\( \rm{d}\)\(\tau\)と書けます。
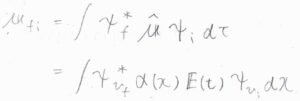
誘起双極子モーメントの式を代入すると、\(\boldsymbol{\mu}_\rm{fi}\)\(=\int \psi_{v_\rm{f}}\)\(^\ast \alpha(x) \boldsymbol{E}(t)\psi_{v_\rm{i}}\)\( \rm{d}\)\(x\)となります。
\(\boldsymbol{E}(t)\)は\(x\)に依存しないので、積分の前に出せます。
ここで、\(x\)は十分小さいものであるとして、\(\alpha(x)\)における二次以上の項を無視して代入します。
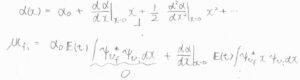
第一項は、波動関数の直交性より\(0\)となり、第二項が零ベクトルになるかどうかは、赤外分光法の個別選択律を考えたときと同様に判別できます。
まず、誘電率\(\alpha\)が結合の伸縮により変化しない場合は、\(\rm{d}\)\(\alpha/\rm{d}\)\(x=0\)であるため、遷移双極子モーメントの大きさは\(0\)になります。
これが選択概律です。
そうならない場合についても、エルミート多項式が満たす漸化式を利用すると、\(v_\rm{f}\)\(\)が\(v_\rm{i}\)\(+1\)もしくは\(v_\rm{i}\)\(-1\)のいずれでもないとき、禁制遷移だとわかります。
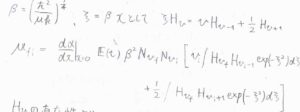
したがって、振動量子数変化\(\Delta v=\pm 1\)となります。
散乱光の波数
回転状態の遷移も考えるとき、それぞれの散乱光の波数は、次のように表されます。
ここでは入射光波数を\(\tilde{\nu}_\rm{i}\)としています。
始めに\(\Delta v=+1\)の場合で考えます。
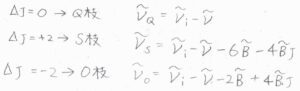
まず、回転量子数が変化しないものをQ枝と呼び、その波数は\(\tilde{\nu}_i-\tilde{\nu}\)となります。
\(\Delta J=+2\)のものはS枝(Sブランチ)と呼び、その波数は\(\tilde{\nu}_i-\tilde{\nu}-6\tilde{B}-4\tilde{B}J\)と書けます。
ただし、ここでは回転定数は振動状態と回転状態に依存しないものとしています。
\(\Delta J=-2\)のものはO枝(Oブランチ)と呼び、波数は\(\tilde{\nu}_i-\tilde{\nu}-2\tilde{B}+4\tilde{B}J\)となります。
\(\Delta v=-1\)の場合については、それぞれの波数の\(\tilde{\nu}\)の前の符号が\(-\)から\(+\)になります。
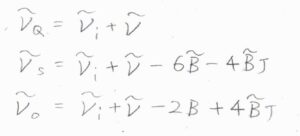
ただし、振動準位間のエネルギーは回転準位間のエネルギーよりとても大きいため、もとの励起状態の占有数が少なく、回転ラマンスペクトルのアンチストークス線ほど相対的に大きな強度のピークは観測されません。
スペクトルの概形
最後、スペクトルの概形はこちらのようになります。
グラフの横軸がラマンシフト\(\Delta \nu\)、縦軸が散乱光の強度\(I\)です。
赤外分光法では、一部の異核二原子分子でのみQ枝が観測されますが、ラマン分光法では同核二原子分子も含めて、すべての二原子分子でQ枝が観測されることになります。
そして、回転定数が振動状態によって変化すると、Q枝が細かく割れたり、図のように構造が現れたりします。
Q枝と両脇にあるピークとの波数の差は\(6\tilde{B}\)であり、それ以外の間隔は\(4\tilde{B}\)となります。
さらに、回転による遠心ひずみが無視できない場合は、\(J\)が大きくなるほど間隔が狭くなっていきます。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました！
