こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(rotation energy level)
それでは内容に入っていきます!
慣性モーメントの定義
慣性モーメントは、回転運動のエネルギーを考えるときに、並進運動での質量と同じように扱われる量です。
定義は、\(\displaystyle I=\sum_im_ix_i^2\)です。
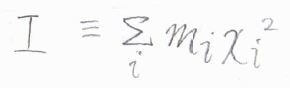
\(i\)が分子を構成する原子を指し、\(m\)は原子の質量、\(x\)は回転軸から原子中心までの距離です。
一般的に、異なる回転軸を選べば、\(x\)が変化するので、慣性モーメントは回転軸ごとに異なる値をもちます。
ただし、対称性の高い分子であれば、回転軸が違っても慣性モーメントが等しくなることもあります。
回転軸\(a\)について回転したときの運動エネルギーを\(E_a\)とすると、\(\displaystyle E_a=\sum_i\frac{1}{2}m_iv_{i, a}^2\)となります。
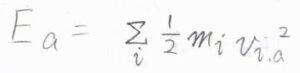
\(v\)は、運動の速さです。
角速度を\(\omega\)とすると、\(v_{i, a}=x_{i, a}\omega_a\)となるため、慣性モーメント\(I_a\)を使うと、\(\displaystyle E_a=\frac{1}{2}I_a\omega_a^2\)と書けます。
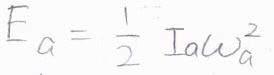
その分子が3つの回転軸\(a\)、\(b\)、\(c\)について自由に回転していた場合は、これらの回転エネルギーの和が全体のエネルギーとなります。
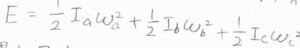
\(I\omega\)を角運動量の大きさ\(L\)と書き換えると、\(\displaystyle E=\frac{L_a^2}{2I_a}+\frac{L_b^2}{2I_b}+\frac{L_c^2}{2I_c}\)とも書けます。
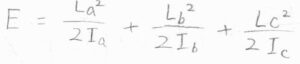
分子の形状と慣性モーメントの関係
ここからは、いくつか分子の形を例として、慣性モーメントの式を見ていきましょう。
二原子分子
まず、最も簡単な二原子分子では、結合ベクトルと平行な回転軸周りの運動では、両方の原子が回転軸上にあるため、慣性モーメントが\(0\)になります。
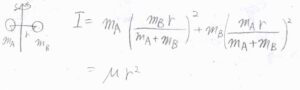
したがって、結合ベクトルに垂直な回転軸についてのみ慣性モーメントが値をもちます。
その値は、換算質量\(\mu\)を使って、\(\mu r^2\)で与えられます。
ここで、\(r\)は結合長です。
三原子直線型分子
三原子直線型分子でも、同じ理由で慣性モーメントは1つだけになります。
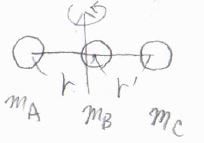
その値は、この図の中の文字を使って、\(m_\rm{A}\)\(r^2+m_\rm{C}\)\(\displaystyle r’^2-\frac{(m_\rm{A}\mathit{r}-\mathit{m}_C\mathit{r}’)^2}{m_\rm{A}+\mathit{m}_B+\mathit{m}_C}\)となります。
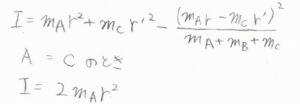
\(\rm{A}\)と\(\rm{C}\)が同じ原子であるときには、2つの結合長も等しくなり、第三項が消えて、\(I=2m_\rm{A}\)\(r^2\)となります。
対称回転子
最後に、対称回転子についてです。
ここでは、クロロメタンやアンモニアのような四面体型の分子を例にします。
対称回転子とは、2つの等しい慣性モーメントと、それとは異なる\(0\)ではない慣性モーメントの値を1つもつ回転子のことを言います。
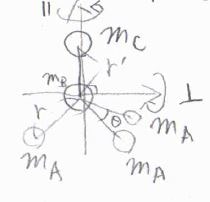
まず、主軸に平行な回転軸について慣性モーメントが求められ、それは\(2m_\rm{A}\)\((1-\cos{\theta})r^2\)で与えられます。
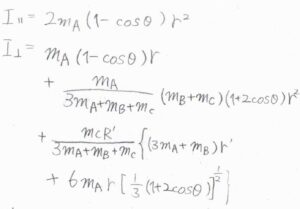
ここで、\(\theta\)は結合角です。
主軸に垂直な2本の回転軸に対する慣性モーメントの値が互いに等しくなり、それはこちらのような形になります。
主軸まわりの回転の慣性モーメントがもう一方の慣性モーメントよりも大きい対称回転子を偏長であるといい、小さい場合は扁平であると言います。
回転エネルギー準位
ここまで古典的な話でしたが、ここからは量子化された回転のエネルギーを考えていきます。
過去に水素原子中の電子について、エネルギーを求めましたが、それと同様に考えていきます。
詳しくは、こちらを参照してください。
分子を剛体であるとして、中心からの距離を固定し、回転軸上にない原子の回転エネルギーを考えます。
\(\nabla^2\)の極座標表示で、いま\(r\)は定数なので第二項と第三項だけ考えます。
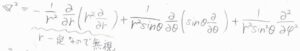
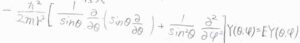
ルジャンドル方程式を解いて得られる答えは、量子数を\(l\)として、\(\displaystyle E=\frac{\hbar^2}{2mr^2}l(l+1)\)となります。
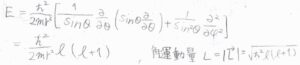
角運動量の大きさLは、\(\hbar \sqrt{l(l+1)}\)で与えられます。
球対称回転子
メタンや六フッ化硫黄などは、3つの等しい慣性モーメントをもっており、これらは球対称回転子と言います。
ベクトルである角運動量の\(x\)、\(y\)、\(z\)成分をそれぞれ\(L_x\)、\(L_y\)、\(L_z\)とすると、これらの二乗の和が\(\hbar^2 J(J+1)\)と書けます。
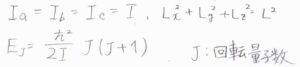
ここではすべての原子を考えたという意味で、先ほどの量子数\(l\)と区別して、\(J\)を量子数としています。
これを回転量子数と呼びます。
全体の回転エネルギー\(E\)は、\(\displaystyle \frac{\hbar^2}{2I}J(J+1)\)となります。
これを波数単位で表すときには、エネルギーを\(hc\)で割ります。

\(c\)は光の速さです。
波数単位のエネルギー\(\tilde{F}(J)\)は、\(\displaystyle \frac{h}{8\pi^2Ic}J(J+1)\)と書けます。
\(J(J+1)\)の前にある値は、回転子の種類に依存する定数であり、これは回転定数と呼ばれます。
ここでは\(\tilde{B}\)と表します。
そして、エネルギー準位の間隔\(E_{J+1}-E_J\)には、大きな特徴があります。
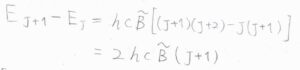
\(2hc\tilde{B}(J+1)\)という形になるのですが、これは\(J\)が増える度に\(2hc\tilde{B}\)ずつ間隔が大きくなるということを表しています。
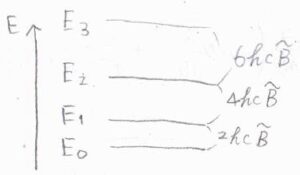
また説明しますが、光の吸収や放出に伴って回転状態の遷移が起こると、スペクトルに等間隔に並んだ複数本のピークが現れます。
この間隔は慣性モーメントの値に反比例するので、一般的に大きな分子になるほど狭くなります。
対称回転子
対称回転子の場合は、慣性モーメントの値が2つあるので、それぞれについて回転エネルギーを考えます。
いま、分子の主軸に平行な直交座標の軸を\(z\)軸とすると、エネルギーはこのように書けます。
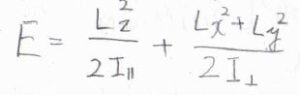
\(L_x^2+L_y^2\)を\(L^2-L_z^2\)と書き換えて整理すると、こちらのようになります。
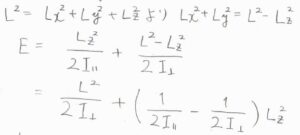
第一項については、先ほどの球対称回転子と同様に回転量子数\(J\)を使って考えることができるので、\(L_z\)について考えればよいことになります。
1つの方向への角運動量を考えるので、極座標で\(\theta\)を固定して\(\phi\)だけが自由に変化することを考えます。
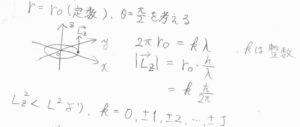
量子条件とド・ブロイ波長の式より、\(L_z\)は\(k\)を整数として、\(k\hbar\)と書けることがわかります。
そして、\(L_z\)は必ず\(L\)よりも小さくなることから、\(k\)の絶対値は必ず\(J\)以下になります。
以上のことより、主軸に平行な回転軸についての回転定数を\(\tilde{A}\)、垂直な回転軸についての回転定数を\(\tilde{B}\)とすると、波数単位のエネルギー\(\tilde{F}(J)\)は、\(\tilde{B}J(J+1)+(\tilde{A}-\tilde{B})k^2\)となります。
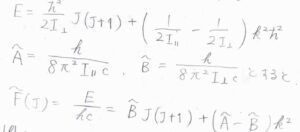
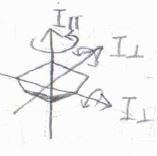
\(k\)の値と対応する回転運動の古典的なイメージは、次の図のようになります。
\(|k|\)が\(J\)に近い値であるとき、全体の角運動量の大きさに対して、\(z\)成分が占める割合が多いことになります。
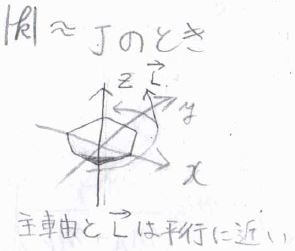
全体の角運動量は主軸に平行とまではいきませんが平行に近く、回転している面は主軸にほぼ垂直になります。
\(k\)が\(0\)というのは、角運動量と主軸が垂直になっているイメージです。
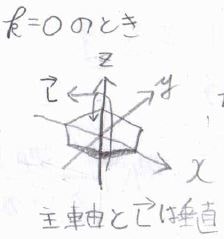
\(k\)が\(-k\)になってもエネルギーには変化がないため、\(k\)が\(0\)以外の状態は二重に縮退します。
直線型回転子
直線型回転子は、対称回転子の特別な例として考えることができます。
主軸まわりにどれだけ回しても慣性モーメントが\(0\)であることから角運動量も\(0\)になるため、\(k\)は\(0\)以外の値をとれないことになります。
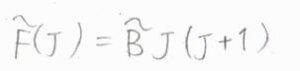
結果、\(\tilde{F}(J)=\tilde{B}J(J+1)\)と球対称回転子とまったく同じ式が出てきます。
球対称回転子は、対称回転子の\(\tilde{A}\)と\(\tilde{B}\)が等しいという特別な例であり、球対称回転子と直線型回転子では、まったく異なる道筋なのですが、結果的に同じ式が導かれることになります。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




