こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(vibrational spectrum of polyatomic molecules 1、vibrational spectrum of polyatomic molecules 2)
独立な振動モードの総数
まず、二原子分子で振動といえば、結合の伸縮を指し、そのほかにはありません。
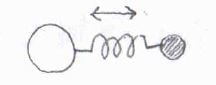
しかし、たとえば直線型の三原子分子では、2つある結合の一方だけが励起されたときに、中心原子の運動が変化するため、もう一方の結合も励起されることになります。
つまり、それぞれの結合の伸縮は、互いに独立な振動モードではありません。
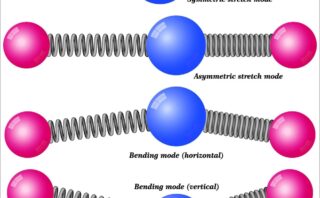
互いに独立な振動モードは、基準振動モードと呼ばれ、こちらに示した対称伸縮、反対称伸縮のように、2つの結合が同時に振動していて、相対的な関係が異なるものになります。
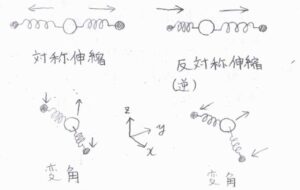
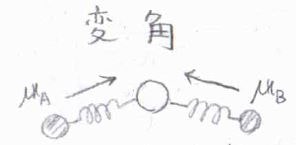
結合角が変化する変角運動も、主軸に対して垂直な二方向に対して考えることができ、これらも独立となります。
基準振動モードの総数は自由度と呼ばれ、直線型の三原子分子の自由度は\(4\)になります。
折れ線型の三原子分子の場合は、対称伸縮と反対称伸縮にくわえて、変角のモードが1つあり、自由度は\(3\)となります。

より一般的に、\(N\)原子分子の場合は、その分子が直線型のときに自由度は\(3N-5\)となり、非直線型のときには\(3N-6\)となります。

たとえば、三次元空間にほかと結合していない\(N\)個の原子があったとき、すべての原子の位置を表すためには、\(3N\)の変数が必要になります。
それらはすべて並進運動の自由度になります。
ここから、原子が結合をつくると、運動が制限されるため、並進の自由度は減少します。
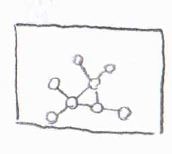
分子1つの並進の自由度は\(3\)であり、残りの\(3N-3\)が分子の内部モード、すなわち振動と回転に割り振られることになります。
そして、直線型分子の配向は、2つの角度変位によって指定することができます。
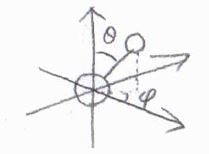
非直線型分子では、さらにもう1つ角度変位が必要になります。
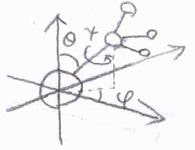
残った自由度が振動に割り当てられ、原子同士の相対的な変位を表すことになります。
したがって、振動の自由度は直線型で\(3N-3-2=3N-5\)、非直線型で\(3N-3-3=3N-6\)となります。
非調和性が無視できるとき、基準振動モードの1つが励起されても、他のモードには作用せず、独立した調和振動子としてふるまいます。
全振動エネルギーは、それぞれの基準振動モードについての振動エネルギーの和になります。
多原子分子の振動基底状態とは、すべての振動量子数が\(0\)の状態を指します。
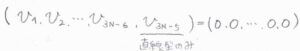
個々の振動エネルギーは、二原子分子のときの式と同じ形ですが、ばね定数と有効質量の違いから、吸収波数に差が生じます。

二原子分子の場合については、こちらを参照してください。

有効質量は、静止している原子を無視して考えます。
たとえば、二酸化炭素の対称伸縮では、中心の炭素原子は静止しているため、有効質量は2つの酸素原子の質量から決まります。
反対称伸縮や変角では、3つすべての原子の質量が寄与します。
また、質量が大きな原子は動きにくいため、軽い原子の運動が基準振動モードの振動数に大きく寄与することになります。
そして、一般的に変角モードの振動数は、伸縮モードの値よりも小さくなるため、エネルギー間隔も伸縮モードの方が大きくなります。
より厳密な話をすると、二酸化炭素は、純粋な伸縮モードと純粋な変角モードが基準振動モードになる分子ですが、これは特殊な例です。
多原子分子の多くでは基準振動モードが伸縮モードと変角モードの混成になります。

先ほどは簡単のために書きませんでしたが、折れ線型の三原子分子の基準振動モードでは、いずれも中心原子は静止しません。
赤外分光法の選択律
ここからは、赤外分光法の話に入っていきます。
まず、基準振動モードに対応する運動によって、双極子モーメントに変化がなければ、そのモードは赤外不活性となります。
これが選択概律です。
たとえば、二酸化炭素の対称伸縮では、それぞれの結合の双極子モーメントが常に打ち消しあうため、分子全体では双極子モーメントをもたず、赤外不活性となります。
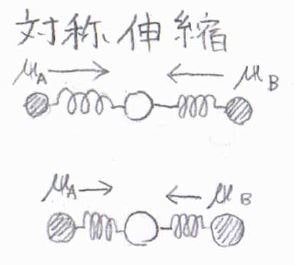
対して、反対称伸縮や変角では、振動によって分子全体の双極子モーメントが繰り返し変化するため、赤外活性となります。
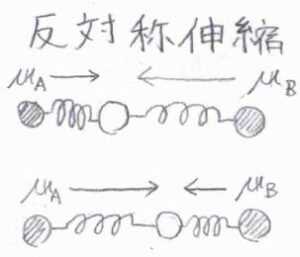
反対称伸縮では、双極子モーメントが主軸に平衡となるのに対して、変角では主軸に垂直となります。
これらの運動に関係する遷移は、スペクトルにおいて、それぞれ平行バンドと垂直バンドとして分類されます。
そして、調和近似のもとでの個別選択律は、それぞれの振動量子数の変化が\(+1\)または\(-1\)の遷移が許容されるというものです。
たとえば、赤外活性な基準振動モードを3つもつ分子の振動状態を\((v_1, v_2, v_3)\)と表すことにすると、そのスペクトルは、\((1, 0, 0)\leftarrow (0, 0, 0)\)と\((0, 1, 0)\leftarrow (0, 0, 0)\)と\((0, 0, 1)\leftarrow (0, 0, 0)\)の3つの遷移を特徴にもつことになります。
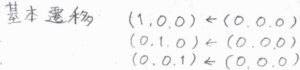
これらの遷移を基本遷移と言います。
非調和性が無視できないときには、\((2, 0, 0)\leftarrow (0, 0, 0)\)などといった倍音が現れます。

\((1, 1, 0)\leftarrow (0, 0, 0)\)のように2つ以上の基準振動モードが励起される遷移も許容されます。
多原子分子の回転スペクトル
最後に、多原子分子の回転運動について、補足をします。
ほとんどの多原子分子は非対称回転子であり、気相のスペクトルは非常に複雑な構造を示します。
それに対して、凝集相、すなわち固相や液相では、分子が自由に回転できないために、むしろ単純なスペクトルを与えます。
横軸を吸収波数としたスペクトルの幅を寿命幅といい、\(\delta \tilde{\nu}\)と表すことにすると、\(\displaystyle \delta \nu\approx \frac{1}{2\pi c \tau}\)と書けます。
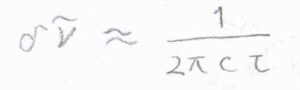
\(\tau\)はその状態の寿命で、寿命が短いほど量子力学的効果によりエネルギーを正確に特定できなくなります。
液相では、およそ\(10^{13}\ \rm{s}\)\(^{-1}\)という高い頻度で分子の衝突が起こり、そのたびに乱雑に配向が変化するため、回転状態の寿命がきわめて短くなります。
乱雑な配向の変化は、タンブリングと言います。
分子が衝突したとき、仮に\(10\%\)の確率で回転遷移が起こるとき、寿命は\(10^{-12}\ \rm{s}\)程度であり、寿命幅はおよそ\(5.3\ \rm{cm}\)\(^{-1}\)となります。
回転定数と同程度のオーダーであることから、吸収のピークは互いに重なりあって、あいまいになります。
そうなると、かえって振動のモードだけをきれいに観測できることになります。
その吸収波数と吸光度は、分子の種類が変わっても、同じ官能基をもっていれば、ほとんど変化しないため、赤外分光法は化合物の同定に利用されます。

このことは、非常に大きな分子であっても基準振動モードが小さな基の原子の運動に支配されている場合が多いことを示しています。
実際の化学分析の方法については、過去の記事で解説していますので、そちらを参照してみてください。
赤外活性とラマン活性
ここからは、ラマン分光法についても考えていきます。
まずは、赤外活性な基準振動モードとラマン活性な基準振動モードをどのように見分けるのかという話からします。
基本は二原子分子のときにお話ししたとおり、双極子モーメントが変化する運動であれば赤外活性、分極率が変化する運動であればラマン活性となります。
原子の集団的な振動でこれらを判別するためには、分子の対称性が重要になるため、点群で整理できます。
交互禁制律(相互禁制律)
特に、対称中心を持っていたときには、赤外活性なモードはラマン不活性であり、ラマン活性なモードは赤外不活性となることがよく知られています。
これを交互禁制律もしくは相互禁制律と言います。
ただ、この交互禁制律はどちらにも不活性となる振動モードの存在を否定していないので、例えば、赤外不活性だからラマン活性だということはできません。
例えば、二酸化炭素の対称伸縮では双極子モーメントは変化しないので赤外不活性であり、絶えず電子密度が変化しているので、ラマン活性となります。
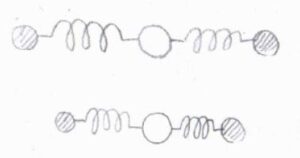
どちらにも活性とはなりません。
また、反対称伸縮では双極子モーメントが変化するため赤外活性であり、ただちにラマン不活性とわかります。
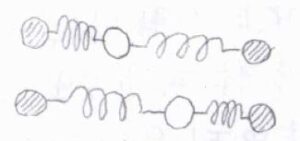
そのほか2つの変角モードも赤外活性であるため、ラマン不活性となります。
これはあくまで分子が対称中心をもっている場合のみであり、メタンや水などの分子には、交互禁制律は適用できません。
関数の積の積分と対称性
ここからは、より一般的な分子について、赤外活性とラマン活性の判別方法を説明していきます。
過去に指標表の利用方法についてお話ししたときに、対称種は関数の積が\(0\)になるかどうかの判別に使うことができるといいました。
詳しくは、こちらを参照ください。

おさらいすると、3つの関数の積\(f_1f_2f_3\)を全空間について積分して得られる値を\(I\)としたとき、\(f_1f_2f_3\)が対称種\(\rm{A}_1\)を張る成分を含まなければ、\(I=0\)となります。
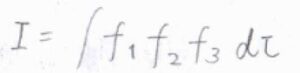
これを利用して遷移双極子モーメントの大きさが\(0\)となれば、禁制遷移だとわかります。
\(f_2\)に電気双極子モーメント演算子を入れて活性を判別するのは、結局\(\psi_{v_\rm{f}}\)\(^\ast x \psi_{v_\rm{i}}\)、\(\psi_{v_\rm{f}}\)\(^\ast y \psi_{v_\rm{i}}\)、\(\psi_{v_\rm{f}}\)\(^\ast z \psi_{v_\rm{i}}\)の対称種を考えることと同じになります。
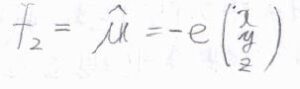

以上のことより、次のことが言えます。
赤外活性の判別方法
ある基準振動モードの対称種が\(x\)、\(y\)、\(z\)のいずれかが張る既約表現の対称種と同じとき、そのモードは赤外活性となります。
\(x\)軸方向に振動する調和振動子を考えてみると、基底状態では波動関数が\(\exp{(-x^2)}\)に比例し、第一励起状態では\(x\exp{(-x^2)}\)に比例します。
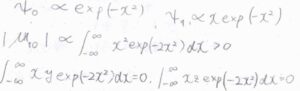
\(x\)軸方向について遷移双極子モーメントを考えると、これは偶関数の積分であることから\(0\)ではない大きさをもつことがわかります。
ただ、\(y\)軸方向、\(z\)軸方向については、\(x\)についての奇関数の積分となることから、積分は\(0\)となります。
波動関数と同じ対称性をもつ軸の方向だけ遷移が許容され、励起後の波動関数も同じ対称性をもつということになります。
ラマン活性の判別方法
そして、ラマンについては、分極率の性質から、\(x^2\)や\(xy\)などといった二次形式の対称種と同じ対称種を張る基準振動モードが活性となります。
実際にこれらの判別方法を使うと、次のようになります。
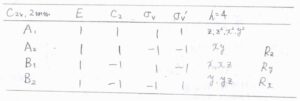
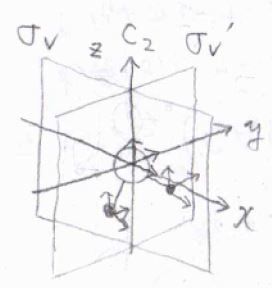
ここでは、\(C_\rm{2v}\)群に属する水を例にして、こちらの指標表をもとに考えていきます。
まず、3個ある原子の位置を指定するためには、9つの座標が必要になります。

それらは、並進に3つ、回転に3つ、振動に3つと割り当てられます。
いま注目したいのは、基準振動モードの張る対称種なので、並進や回転を取り除いて、考えなくてはいけません。
9つの座標について、対称操作によって変化がないものを\(1\)、符号が変化したものを\(-1\)、それ以外を\(0\)として数えると、指標は左から順に\(9, -1, 1, 3\)となります。
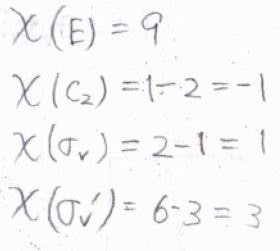
直積の分解をすると、\(3\rm{A}\)\(_1+\rm{A}\)\(_2+2\rm{B}\)\(_1+3\rm{B}_2\)となります。
直積の分解についても、同じ記事で解説しています。

指標表を見て、\(x\)、\(y\)、\(z\)の対称種から並進の張る対称種は\(\rm{A}\)\(_1+\rm{B}\)\(_1+\rm{B}_2\)であり、回転は\(R_x\)、\(R_y\)、\(R_z\)の対称種から\(\rm{A}\)\(_2+\rm{B}\)\(_1+\rm{B}_2\)となります。
これらを引くと、3つの振動モードの張る対称種は\(2\rm{A}\)\(_1+\rm{B}_2\)だとわかります。
\(\rm{A}_1\)、\(\rm{B}_2\)はそれぞれ\(z\)、\(y\)と同じ対称種を張ることから、これら3つの基準振動モードはすべて赤外活性と判別できます。
また、\(z^2\)や\(yz\)といった二次表現の対称種とも同じであることから、すべてラマン活性となります。
お持ちの教科書に書いてある指標表を見ていただくと、反転中心をもつ\(C_\rm{i}\)群や\(D_\rm{\infty h}\)群、\(O_\rm{h}\)群などは、一次形式と二次形式で既約表現の対称種が異なります。
ここから、赤外活性なモードはラマン不活性であり、ラマン活性なモードは赤外不活性であるといえます。
偏光解消
ここからは、ラマン効果を改良した測定法について、お話ししていきます。
まず、入射光に偏光を用いると、その基準振動モードの帰属に役立つ情報が得られることがあります。
ラマン散乱光のうち、入射光の偏光面に対して平行に偏光したものの強度と垂直に偏光したものの強度の比を偏光解消度\(\rho\)と定義します。

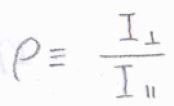
\(\rho=0\)は、ラマン散乱により偏光に変化がなかったことを意味します。
偏光が完全に解消されたときには、\(\rho=1\)です。
一般的に、\(\rho\)がだいたい\(0.75\)以上の値となったときに、偏光解消されたと言います。
たとえば、水の反対称伸縮を主とする基準振動モードでは、振動運動に伴って二方向について電子密度の変化が生じます。

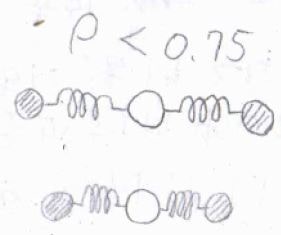
このような場合に、偏光解消が起こります。
共鳴ラマン分光法
ラマン散乱の過程は、いったん仮想状態まで励起された後に、遷移後の状態まで緩和されるというものでした。
この仮想状態は複数の電子状態の組み合わせとして考えたもので、実際にこの状態が存在しなくても、干渉性の散乱は起こります。
ただ、実際の電子遷移の振動数に近い入射光を用いると、特定の振動モードでのみ共鳴することで著しく大きな強度の散乱光を得ることができます。
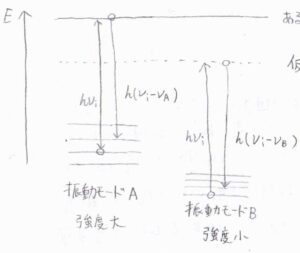
これを利用すると、振動モードが多数存在するような試料でも、単純化されたスペクトルを得ることができます。
一般的に、生体試料を測定する際には、基質にくわえて、酵素のアミノ酸残基や修飾、そしてその周りにある水分子もスペクトルに影響を及ぼすので、非常に複雑なスペクトルを与えます。

入射光の振動数を変化させて共鳴ラマン効果を利用すると、たとえば、酵素と会合した色素の振動モード由来のピークを選択的に観測することができます。

コヒーレントアンチストークスラマン分光法(CARS)
まず、装置図はこちらの図のようなものを使います。
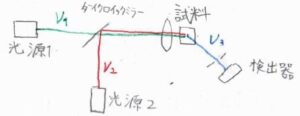
振動数の異なる2つのレーザー光を試料に照射して、散乱される光を検知します。
レーザー光は時間的、空間的にほぼコヒーレントな光と言われており、その優れた単色性や指向性、集束性といった性質が利用されています。
ここでは、光源\(1\)のレーザー光をポンプ光、光源\(2\)のレーザー光をストークス光と呼びます。
この散乱現象は、こちらの図で示したような過程を経ます。
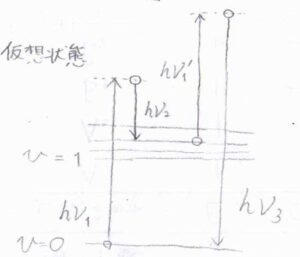
まず、ポンプ光によって仮想状態へと励起されたのちに、振動遷移後の状態へ緩和します。
\(\nu_1-\nu_2\)が分子がもつ振動モードの振動数と一致したとき、すなわち\(\nu_2\)が仮想状態と緩和後のエネルギー差に相当する振動数であったときに共鳴します。
このとき、多数の分子で位相がそろったまま振動が起こります。
ここから、新たにストークス光以外の光と干渉することで、振動数の異なる散乱光を放出します。
図の中で、\(\nu_1\)と\(\nu_1’\)は必ずしも同じ値である必要はありませんが、多くの場合はポンプ光をそのまま利用します。
このとき、散乱光の振動数\(\nu_3\)は\(2\nu_1-\nu_2\)となります。
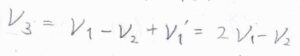
\(\nu_2\)がストークス線の振動数で\(\nu_1-\Delta \nu\)と表されるとき、\(\nu_3=\nu_1+\Delta \nu\)となります。
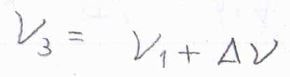
つまり、アンチストークス線の振動数と同じ光を、大きな強度で観測することができます。
\(\nu_1\)は固定したまま、\(\nu_2\)を変化させることでラマンスペクトルを得ることができます。
この測定をする最大のメリットは、バックグラウンド、すなわち非干渉の散乱光やホワイトノイズを取り除いて、ラマン遷移を研究できることにあります。
散乱角は、位相整合条件より波数ベクトル\(2\boldsymbol{k}_1-\boldsymbol{k}_2\)の方向で決まります。
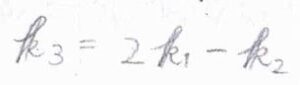
レーザー光のコヒーレンスのために、指向性のよい散乱光を得られるため、スリットを通して目的の散乱光だけを検知することができます。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!