こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマは、こちら!
それでは内容に入っていきます!
ガウス鎖の復習
まずは、ガウス鎖の復習から入ります。
ガウス鎖とは、両末端間距離の分布関数がガウス分布になる鎖のことを言います。
自由連結鎖や自由回転鎖、束縛回転鎖といった高分子のモデルは、すべてガウス鎖モデルに含まれます。
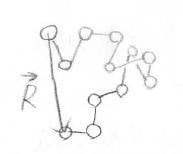
これらのモデルでは、分子内の排除体積効果を考えていません。
ここに関しては、過去の記事でお話ししているので、そちらを参照してください。


そして、3次元空間におけるガウス鎖の両末端間距離の分布は、\(4\pi r^2P(r)\)で与えられます。
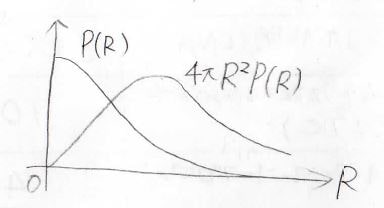
ここで、\(P(r)\)は規格化した一次元のガウス分布で、\(n\)は結合ベクトルの本数、\(b\)は結合長です。

\(C_\infty\)は特性比という量で、自由連結鎖について\(1\)になります。
結合角や内部回転ポテンシャルの影響を反映して、\(0\sim 1\)までの値をとります。
補足
ここで、ガウス鎖についての注意事項として、以前の記事で説明できていなかった部分を補足させてください。
まず、ガウス分布は常に\(0\)より大きい値となるため、引っ張った自由回転鎖の長さ\(\displaystyle nb \sin{(\frac{\theta}{2})}\)よりも長い両末端間距離をとってもよいことになります。
これは現実的ではないので、Langevin(ランジュバン)関数の逆関数\(L^{-1}(x)\)を使って補正するという方法があります。

そして、ガウス鎖では\(n\)がとても大きいとしているため、部分鎖もガウス鎖になる一種のフラクタル図形と考えることができます。

ここで、部分鎖は1本の鎖を\(n_\rm{s}\)等分したものであるとしています。
しかし、実際には部分鎖1つの結合数\(\displaystyle \frac{n}{n_\rm{s}}\)が\(50\)より小さくなってきたところで、非ガウス性が現れると言われています。
また、大きく変形された高分子でも、非ガウス性は顕著になります。
そして、多変数のガウス分布関数を使って、より厳密な計算をすると、実はガウス鎖は完全な球ではなく回転楕円体となります。
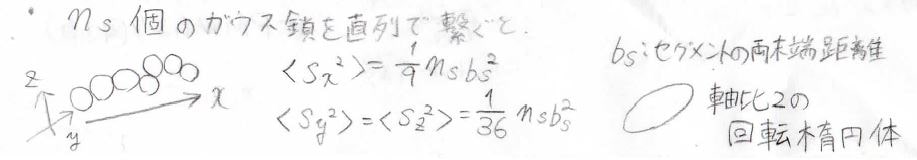
ここで、\(b_\rm{s}\)は1つのセグメントの平均両末端間距離で、末端間ベクトルに平行な方向を\(x\)軸方向、垂直な方向を\(y\)、\(z\)軸方向としています。
それぞれの平均二乗回転半径は、上のように計算されるため、軸比が\(2\)の回転楕円体とみなせます。
みみず鎖モデル
ガウス鎖の話はここまでとして、次の話に入っていきます。
これまで考えてきた高分子のモデルはすべて、有限個のビーズが繋がってできた鎖を考えていました。
しかし、この鎖はカクカクしてるので、鎖に沿って微分することができないなど、数学的な取り扱いが難しいです。

そこで、連続曲線として高分子を表すのがみみず鎖モデルです。
これは、結合数\(n\)、結合長\(b\)、結合角\(\theta\)の自由回転鎖について、\(n \rightarrow \infty\)、\(b \rightarrow 0\)、\(\theta \rightarrow \pi\)の極限をとったものです。
とても小さいビーズが無限につながって、グニャグニャしてるイメージです。
このような極限を考えると、もはや結合数や結合長、結合角のような概念は存在せず、別の長さパラメータ2つで平均二乗両末端間距離や平均二乗回転半径が表されるようになります。
そのパラメータの1つは、鎖を一直線状に引っ張ったときの長さ\(nb\)で、文字は\(L\)を使うことにします。
そして、もう1つは\(\displaystyle \frac{b}{1+\cos{\theta}}\)で、文字は\(q\)と表すことにします。
\(L\)は経路長と呼びますが、中には全長と表記している教科書もあります。
\(q\)は持続長と呼ばれます。
経路長と持続長を用いて、平均二乗両末端間距離を表した式は、次のように導かれます。
まず、自由回転鎖の平均二乗両末端間距離は、\(n^0\)の項までで近似すると、このようになります。
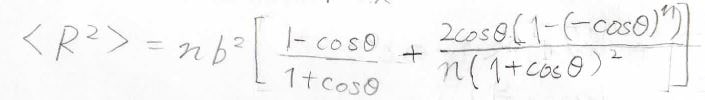
導出の過程は煩雑ですが、下にpdfを貼っておくので、気になる人だけ見ておいてください。
Gause chain mean-squared end to end distance derivation
結合角\(\theta\)を\(\pi\)に近づけていったときの極限を考えると、鎖の方向に対する微分ができるので、数学的に扱いやすくなります。
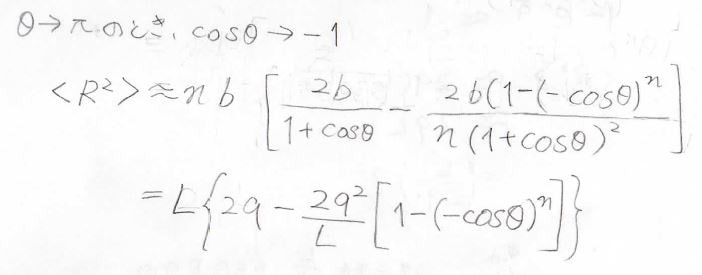
すると、第一項は\(2qL\)になります。
そして、第二項については、\(\displaystyle -\cos{\theta}=1-\frac{L}{nq}\)と書き換えることで、下のように整理できます。
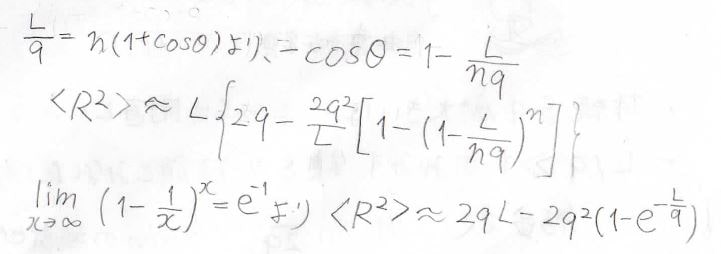
大かっこの中にネイピア数\(\rm{e}\)の定義が見いだせるので、\(n\)を無限大にしたとき、ここは\(\displaystyle \exp{(-\frac{L}{q})}\)となります。
したがって、みみず鎖の平均二乗両末端間距離は、\(\displaystyle 2qL-2q^2[1-\exp{(-\frac{L}{q})}]\)と書けます。
高分子の剛直性
持続長\(q\)とは、高分子の剛直性を表すパラメータです。
例えば、\(L\)に対して\(q\)がとても大きい場合には、\(\displaystyle \exp{(-\frac{L}{q})}\)のテイラー展開を二次の項までとることで\(\langle R^2\rangle\approx L^2\)と近似されます。

両末端間距離は、多少の分布をもつものの、高い確率で経路長\(L\)に近い値をとることから、まっすぐ伸びた形をとりやすいことになります。
反対に、経路長\(L\)に対して\(q\)が無視できるほど短かった場合、\(\langle R^2\rangle\approx 2qL\)と近似できます。

変形すると、\(\displaystyle \frac{L}{2q}q^2\)とも書けます。
これは、結合数が\(\displaystyle \frac{L}{2q}\)で、結合長が\(q\)の自由連結鎖の平均二乗両末端間距離と一致します。
以上のことから、持続長\(q\)は高分子の曲がりにくさ、つまり剛直性を表すパラメータだということになります。
\(q\)が長いほど、高分子は剛直であることになります。
また、\(q\)が短いみみず鎖をガウス鎖としてみなすと、その結合数は\(\displaystyle \frac{L}{2q}\)、実効の結合長\(\sqrt{C_{\infty}}b\)は\(2q\)となります。
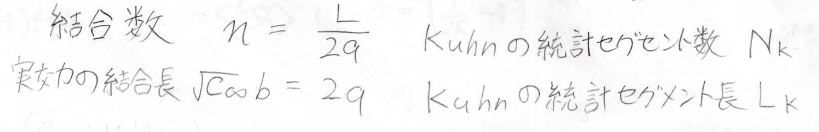
これらはそれぞれKuhn(クーン)の統計セグメント数、Kuhnの統計セグメント長と呼ばれており、\(N_\rm{K}\)、\(L_\rm{K}\)といった文字で表されることが多いです。
高分子の剛直性を表すパラメータとして、持続長\(q\)ではなく、Kuhnの統計セグメント長\(L_\rm{K}\)が使われることもあります。
実際に、現実の高分子と比較したときには、剛直であるほどセグメント同士の衝突確率が低いため、分子内排除体積効果がはたらきにくく、みみず鎖の予想が現実と一致しやすいことが知られています。
逆に、良溶媒中の屈曲性高分子は、両末端間距離の分布がガウス分布から外れるため、みみず鎖モデルと一致しなくなります。
持続長の例
実際の持続長は、下の表のようになります。

一般的に、単結合だけで主鎖が構成されるポリスチレンなどに比べて、らせん構造や共役二重結合を有する高分子のほうが持続長は長くなります。
らせん構造をとる高分子にみみず鎖モデルをあてはめるときには、経路長\(L\)を主鎖に沿った長さではなく、らせん軸の長さとしてとるため、注意が必要です。
そして、3重らせん構造をとる多糖のシゾフィランやたんぱく質のコラーゲンは、持続長が\(100\ \rm{nm}\)のオーダーになります。
ポリ(γ-ベンジルL-グルタメート)、略してPBLGは、タンパク質同様に\(\displaystyle \alpha\)-ヘリックス構造をとり、その持続長は\(150\ \rm{nm}\)程度となります。
二重らせん構造で知られるDNAも、持続長\(60\ \rm{nm}\)などになります。
多糖誘導体であるセルロース(トリスフェニルカルバメート)、略してCTCもポリスチレンなどと比べて剛直で、持続長は\(10\ \rm{nm}\)です。
その下のポリ(1-フェニル-1-プロピン)は、長い\(\displaystyle \pi\)電子共役系となるポリアセチレン誘導体で、平面構造をとろうとするため、剛直になります。
剛直性による分類方法
剛直性による高分子の分類は、持続長を直接使うわけではなく、持続長と経路長の比によって考えられます。
持続長が長い、あるいは経路長が短いとき、高分子は剛直な鎖として振る舞い、その逆では屈曲しやすい鎖になります。
それぞれは剛直高分子、屈曲性高分子と呼ばれます。
剛直高分子は、強靭な材料や光学材料などに利用されています。
屈曲性高分子は、ビニール袋のポリエチレンや化粧品などに使われるポリエチレングリコール、あとはポリスチレンなど、身の回りでもよく見るプラスチック製品の多くに使われています。
そして、持続長と経路長が同程度である高分子は、半屈曲性高分子と呼ばれ、その物理的な取り扱いにはまだまだ謎が多いです。
コラーゲンや多糖、DNAなど生体高分子の多くがこの半屈曲性高分子に分類されており、これらの物理的性質の解明は生物学的にも大変重要であるため、今も盛んに研究されています。
側鎖による持続長への影響
側鎖の影響も重要になることがあります。
例えば、ポリシラン誘導体では持続長が\(5\sim 100\ \rm{nm}\)の範囲で大きく上下します。
立体規則性も大きく影響することがあり、例えば、シンジオタクチックポリメタクリル酸メチル(s-PMMA)は溶媒中で少しだけらせん状になります。

これは、側鎖のメチル基とカルボキシル基の立体反発を避けるためです。
らせんを巻くと剛直になるので、らせんを巻かないアタクチックポリメタクリル酸メチル(a-PMMA)よりも持続長は長くなります。
とは言っても、DNAのように水素結合で固定化されてはいないので、完全に規則的ならせん構造をとっているわけではありません。
このような高分子は、らせんみみず鎖というモデルで議論されます。
練習問題
それでは最後、練習問題をやって終わります。
記事の中で、みみず鎖の平均二乗両末端間距離は求めたので、平均二乗回転半径を求めてみましょう。
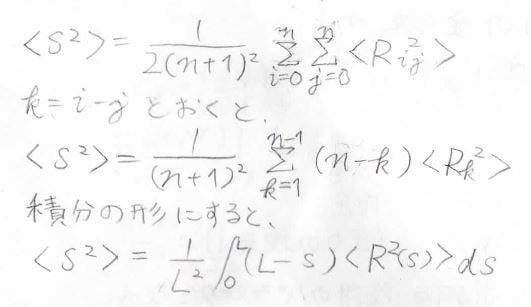
詳しい説明は、以下の記事でしているので割愛しますが、回転半径と両末端距離の関係を積分の形で表すと上のようになるので、この式から回転半径の式を求めてください。

ここで、\(s\)は一方の末端からとある点まで、経路に沿った距離です。
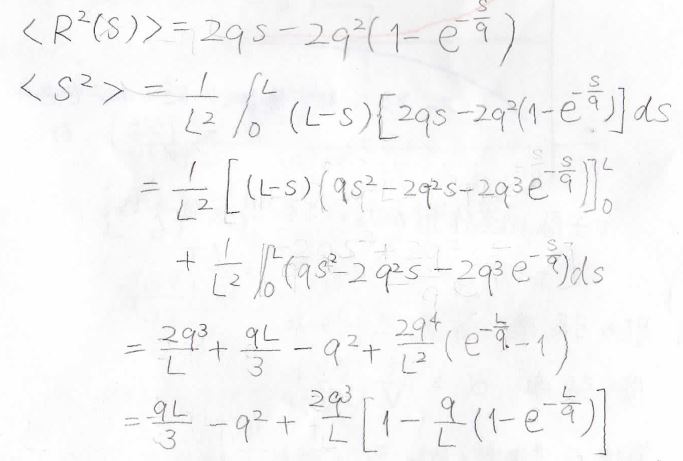
まず、\(\displaystyle \langle R^2(s)\rangle =2qs-2q^2[1-\exp{(-\frac{s}{q})}]\)を代入します。
そして、部分積分の公式を使って整理すると、\(\displaystyle \langle S^2 \rangle =\frac{qL}{3}-q^2+\frac{2q^3}{L}\{1-\frac{q}{L}[(1-\exp{(-\frac{L}{q})}]\}\)と導かれます。
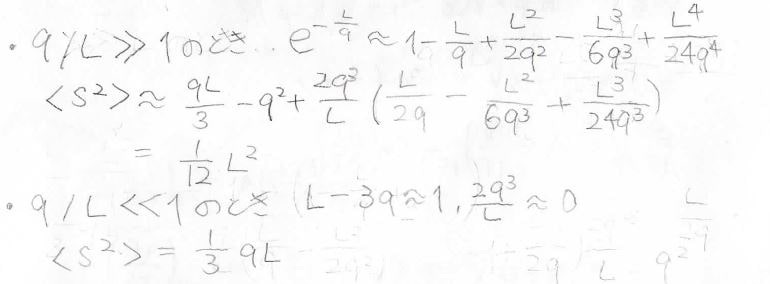
ちなみに剛直極限では、指数関数部分を\(4\)次の項まで近似することで、\(\displaystyle \langle S^2\rangle =\frac{L^2}{12}\)となります。
屈曲性高分子として極限をとる場合には、\(\displaystyle \langle S^2\rangle =\frac{qL}{3}\)となり、平均二乗両末端間距離\(2qL\)の\(\displaystyle \frac{1}{6}\)倍になっていることが確認できます。
この結果は、持続長の短いみみず鎖がガウス鎖として考えられることと矛盾しません。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




