こんにちは!
それでは今回も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(hybrid orbital)
それでは内容に入っていきます!
混成軌道って何?
はじめに、混成軌道とは何かというところからお話しします。
混成軌道とは、原子が結合を作るときに、最終的に一番大きな安定化が得られるように、元からある原子軌道を組み合わせてできる新しい軌道のことを言います。
とは言っても、実際に軌道が組み合わされる現象が観測されるわけではなく、原子の価数や立体構造を理解するうえで便利な考え方として受け入れられている概念だと考えてください。
例えば、高校で炭素原子の腕の本数は4本と習います。
しかし、共有結合を作るためには1個ずつ電子を出し合わないといけないため、電子が1個だけ占有している軌道でないと共有結合を作ることはできないはずです。
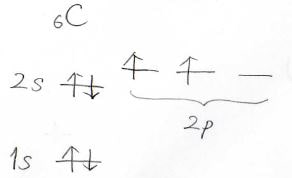
炭素原子の電子構造を見ると、そんな軌道は2つしかありません。
すなわち、このままでは2本までしか結合をつくることができません。
どうやって4本の結合ができるのだろうかという疑問に、もっともらしい解釈を与えてくれるものこそが、今回お話しする混成軌道という概念です。
ここからは、混成軌道の例を実際に見ていきましょう!
混成軌道の例
もう一度繰り返しになりますが、混成軌道とは原子軌道を組み合わせてできる軌道のことですから、どういう風に組み合わせるのかということに注目しながら、読み進めてください。
よく出てくる、軌道を組み合わせるパターンは全部で3つあります。
それぞれは何方向に結合を作るのかという違いだと、ひとまずは考えてください。
\(\displaystyle \rm{sp}\)\(^3\)混成軌道
まず、4方向に結合を作る場合を見てみましょう。
混成軌道を考えるとき、始めにすることは昇位です。

\(\displaystyle 2\rm{s}\)軌道の電子を1つ、空の\(\displaystyle 2\rm{p}\)軌道に移して、主量子数2の4つの軌道を電子が1つずつ占有する形を作ります。
一般的に、\(\displaystyle 2\rm{s}\)軌道は\(\displaystyle 2\rm{p}\)軌道よりも少しエネルギーが小さいため、昇位はエネルギー的に不利な現象なのですが、ここでは最終的に結合を作った時に最安定となることを目指しています。
そして、1つの\(\displaystyle \rm{s}\)軌道と3つの\(\displaystyle \rm{p}\)軌道を混合して、エネルギー的に等価な4つの軌道ができたと考えます。

これが混成です。
このようにしてできた軌道は、1つの\(\displaystyle \rm{s}\)軌道と3つの\(\displaystyle \rm{p}\)軌道からできているという意味で、\(\displaystyle \rm{sp}\)\(^3\)混成軌道と呼びます。
個々の軌道の形は、位相の強め合いと打ち消しあいで、下のようになります。

これらが空間中に配置されるときには電子間で生じる静電反発が最も小さい形をとろうとします。
4方向に伸びる場合にはこのように四面体型が最も安定な構造になります。

2つの\(\displaystyle \rm{sp}\)\(^3\)軌道がなす角は、およそ\(\displaystyle 109.5^\circ\)になります。
\(\displaystyle \rm{sp}\)\(²\)混成軌道
3方向に結合を作る場合には、先ほどと同様に昇位した後に1つの\(\displaystyle \rm{s}\)軌道と2つの\(\displaystyle \rm{p}\)軌道で混成が起こり3つの\(\displaystyle \rm{sp}\)\(^2\)混成軌道ができます。


これらが静電反発を避けるためにはまず、等価な3つの\(\displaystyle \rm{sp}\)\(^2\)軌道が、正三角形を作るように結合角約\(\displaystyle 120^\circ\)で3方向に伸びます。
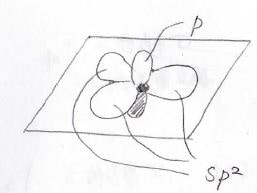
その後、残った\(\displaystyle \rm{p}\)軌道が3つの\(\displaystyle \rm{sp}\)\(^2\)軌道との反発を避けるように、3つの\(\displaystyle \rm{sp}\)\(^2\)混成軌道がなす平面と垂直な方向を向いて位置することになります。
\(\displaystyle \rm{sp}\)混成軌道
2方向に結合を作る場合には、昇位の後、\(\displaystyle \rm{s}\)軌道と\(\displaystyle \rm{p}\)軌道が1つずつ混ざり合って2つの\(\displaystyle \rm{sp}\)混成軌道ができます。


2つの\(\displaystyle \rm{p}\)軌道は、そのまま残ります。
空間上に配置するときにはまず等価な2つの\(\displaystyle \rm{sp}\)軌道が反発を避けるため、同一直線上の逆方向に伸びていきます。
残った2つの\(\displaystyle \rm{p}\)軌道は、その直線に対して垂直な方向に向きます。

また、\(\displaystyle \rm{p}\)軌道同士でも垂直になるはずなので、このような配置になります。
化合物の立体構造
ではここからは、この混成軌道のルールを使って化合物の立体構造を予想してみましょう。
どの混成軌道か見分けるための重要なポイントは、注目している原子の周りで\(\displaystyle \sigma\)結合と孤立電子対が合わせていくつあるかということです。
共有結合の様式については、こちらの記事で詳しく解説しています。
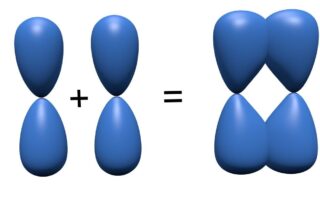
先ほどは、わかりやすさのために、結合が何方向に伸びているかということで説明しましたが、より正確には何方向に電子対が広がりをもつのかを考える必要があります。
アンモニア
まず、アンモニアを例に立体構造を考えてみましょう。
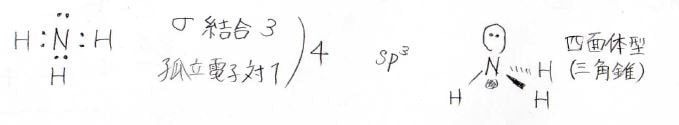
アンモニアの窒素原子に着目すると、\(\displaystyle \sigma\)結合が3本、孤立電子対数が1つあります。
混成軌道を考える際には、これらの合計数が重要になります。
この場合は4なので\(\displaystyle \rm{sp}\)\(^3\)混成となり、四面体型に電子が配置します。
窒素原子と水素原子のみに着目した場合には、高さが低い四面体型、すなわち三角錐になります。
孤立電子対があるので、正四面体型の分子とは言えません。
そこだけ注意しましょう。
水
続いて、水分子の場合も考えてみましょう。

酸素原子について、\(\displaystyle \sigma\)結合が2本と孤立電子対が2つあります。
これらの和は4であるため、これも\(\displaystyle \rm{sp}\)\(^3\)混成になります。
水素原子と炭素原子のみに着目すると折れ線型の分子になりますが、孤立電子対も考えると四面体型になります。
ただし、実際の水分子の結合角は\(\displaystyle 104.5^\circ\)であり、正四面体型で想定される\(\displaystyle 109.5^\circ\)とは乖離があります。
これは、孤立電子対間の静電反発が共有電子対のものよりも大きいのが理由です。
エチレン
次に、エチレンの炭素原子について考えてみましょう。

\(\displaystyle \sigma\)結合は3本、孤立電子対は0で、その和は3になります。
このときには、\(\displaystyle \rm{sp}\)\(^2\)混成となり、平面構造になります。
この平面に垂直な方向に\(\displaystyle \rm{p}\)軌道があり、隣接している炭素原子との間で\(\displaystyle \pi\)結合を作っています。
二酸化炭素
では最後、二酸化炭素の炭素原子について考えてみましょう。
\(\displaystyle \sigma\)結合は2本、孤立電対は0です。
その和は2となるため、\(\displaystyle \rm{sp}\)混成となり、このような直線型の構造を取ります。
このように、\(\displaystyle \sigma\)結合の数と孤立電子対数の和を考えれば、その原子の周りの立体構造を予想することができます。
この考え方の例外
ただし、この考え方は万能ではなく、平面構造を取ることで共鳴安定化が起こる場合には通用しないことがあります。
その例は、アミド結合の窒素原子です。

\(\displaystyle \sigma\)結合が3本で孤立電子対が1つあり、その和が4なので\(\displaystyle \rm{sp}\)\(^3\)混成だと考えてしまいがちですが、このように電子が非局在化した方が安定なため、そのために\(\displaystyle \rm{sp}\)\(^2\)混成の平面構造を取ります。
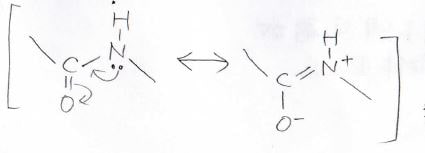
こういった例外がありますので、ぜひ知っておいてください。
練習問題
はい、それでは最後練習問題をやって終わろうと思います。
ここに示す4つの化合物の立体構造を予想してください。
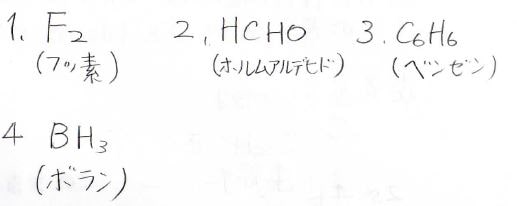
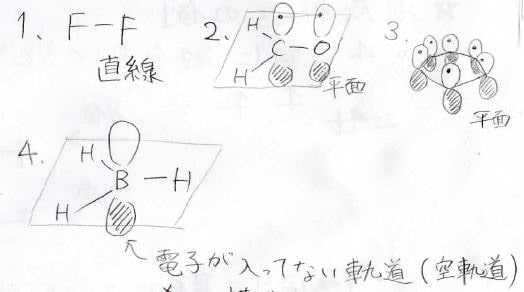
1.
当たり前ですが、すべての二原子分子は直線型になります。
2.
σ結合が3本、孤立電子対が0ということで\(\displaystyle \rm{sp}\)\(^2\)混成となり、平面構造となります。
3.
ベンゼンは、共鳴効果によりとても安定になっています。
もちろん、\(\displaystyle \rm{sp}\)\(^2\)混成で平面構造です。
4.
\(\displaystyle \sigma\)結合3本、孤立電子対0で、合わせて3になるので、\(\displaystyle \rm{sp}\)\(^2\)混成、すなわち平面構造となります。
ここからは補足ですが、ボランのホウ素原子の\(\displaystyle \rm{p}\)軌道には電子が1つも入っていません。
こういった軌道は空軌道と呼ばれ、電子を受け取る能力を有するLewis酸としてはたらきます。
反応性に富む物質であるため、通常はLewis塩基であるTHF(テトラヒドロフラン)溶液にして、安定な状態で売られています。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




