こんにちは！
それでは今日も化学のお話やっていきます。
今回のテーマは、こちら！
動画はこちら↓
動画で使ったシートはこちら(symmetry operation)
それでは、内容に入っていきます！
対称操作とは？
まず、対称操作とは何かを説明します。
対称操作とは、ある図形や立体について、特定の動かし方をした結果、動かす前の形と重なってしまい、見かけ上は何も動かしていないようになる操作のことを言います。
例えば、正三角形について、その重心を中心に\(120^\circ\)回転させると、回転する前とぴったり重なってしまいます。
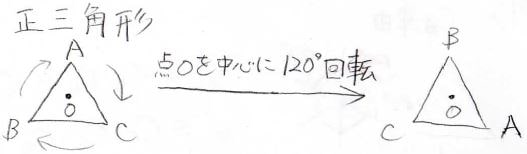
このとき、その回転するという操作は、対称操作であることになります。
分子の対称操作
続いて、分子の対称操作には、どういったものが考えられるのかをお話していきます。
恒等操作
1つ目は恒等操作で、\(E\)と表記します。
恒等というのは、常に同じという意味であり、この操作は何も動かさないという操作になります。
絶対配置を固定するため、どんな立体であっても、恒等操作は対称操作になります。
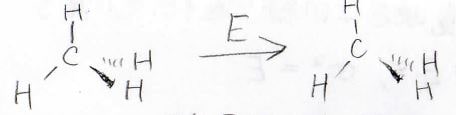
後々またお話しますが、この恒等操作は、群を考えるときの単位元にあたります。
回転操作(本義回転操作)
そして、続いては回転操作で、\(C_n\)と書きます。
これは、本義回転操作とも言います。
ある回転軸を中心とした回転をさせる操作で、何度回転させるかは回転の次数\(n\)の値によって決まります。
\(n=2\)の場合は\(180^\circ\)、\(n=3\)のときには\(120^\circ\)、\(n=4\)であれば\(90^\circ\)といった具合に、\(360^\circ\)を\(n\)で割った角度分だけ回転させます。
例えばベンゼンは、\(60^\circ\)回転させると、元の形と重なる回転軸をもっており、このときベンゼンは\(C_6\)の対称操作をもつことになって、この回転軸のことを\(C_6\)軸とか\(6\)回回転軸などと呼びます。
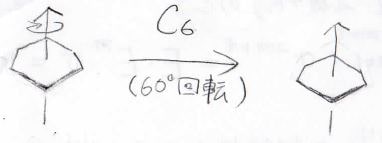
ちなみにベンゼンは、\(C_6\)軸と垂直な方向に\(C_2\)軸があと\(6\)本あり、ここでは炭素原子上を通らない\(3\)本を\(C_2’\)軸、炭素原子上を通る3本を\(C_2^”\)軸と呼ぶことにします。
ここで、分子が複数の対称な回転軸をもっていたとき、最も次数の大きい回転軸のことを主軸と言います。
ベンゼンの場合は、\(6\)回回転軸が主軸になります。
鏡映操作
続いての対称操作は、鏡映です。
これは、ある面を鏡に見立てて、鏡写しにする操作です。
文字は\(\sigma\)を使います。
ベンゼンの場合は、まず主軸と垂直な\(\sigma_\rm{h}\)面を中心とした鏡映が対称操作になります。
その他にも、主軸を含む面として、\(\sigma_\rm{v}\)面を3つと\(\sigma_\rm{d}\)面を3つもちます(添え字の\(\rm{d}\)や\(\rm{v}\)は、\(C_2’\)軸を含むかどうかを区別しています)。
反転操作
次の対称操作は反転です。
さっきの鏡映は面を要素としていましたが、反転は点を要素とします。
例えば、ベンゼンは重心を中心に反転させても元の形と重なるため、反転は対称操作になります。
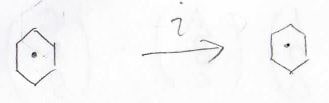
回映操作(転義回転操作)
最後が回映操作です。
転義回転操作とも言い、\(S_n\)と表します。
まず\(\displaystyle n\)回回転させます。
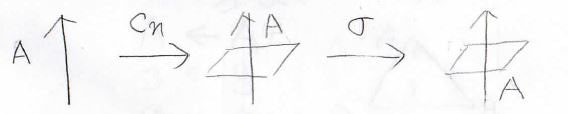
その後、\(n\)回回転軸と垂直な\(\sigma_\rm{h}\)面に対して鏡映をとります。
その分子が\(C_n\)と\(\sigma_\rm{h}\)を対称操作としてもっている場合、最初の回転軸がそのまま\(S_n\)軸となります。
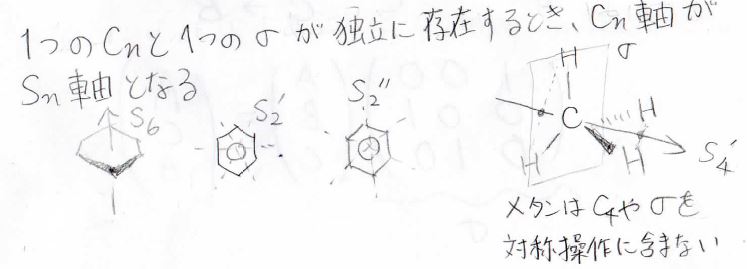
しかし、回転と鏡映を独立にもっていない場合でも、回映が対称操作になることがあります。
例えばメタンの場合、\(3\)回回転軸に垂直な\(\sigma_\rm{h}\)面はありませんが、\(4\)回回映軸をもっています。
この軸は、メタンの水素原子\(4\)つを2組に分けて、それらを繋いだ線分の中点を通るように引かれます。
この際、メタンは\(S_4\)を対称操作にもちますが、\(C_4\)や\(\sigma_\rm{h}\)はありません。
行列としての表現
以上が分子がもちうる対称操作でした。
そして、これらの対称操作には、共通点があって、すべて行列として表現することが可能です。
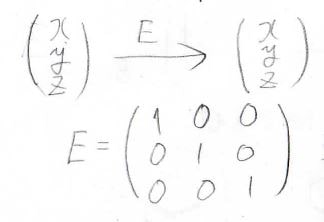
わかりやすいのが恒等操作\(E\)で、これは単位行列になります。
それで、正三角形の頂点に\(\rm{A}\)、\(\rm{B}\)、\(\rm{C}\)と名前をつけておいて、それを\(120^\circ\)反時計回りに回すことを考えると、頂点\(\rm{A}\)は頂点\(\rm{C}\)があった場所へ移り、同様に\(\rm{B}\)は\(\rm{A}\)、\(\rm{C}\)は\(\rm{B}\)に動きます。
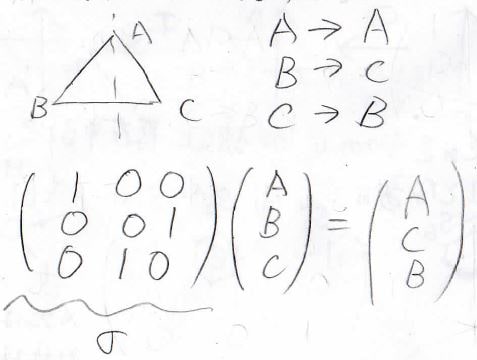
したがって、\(C_3\)は上記のような行列として表現できます。
また、角\(\rm{A}\)の二等分線を含む面に対して、鏡映をとる操作は、\(\rm{A}\)をそのまま、\(\rm{B}\)を\(\rm{C}\)へ、\(\rm{C}\)を\(\rm{B}\)へ移すことになるので、下のような行列として表現できます。
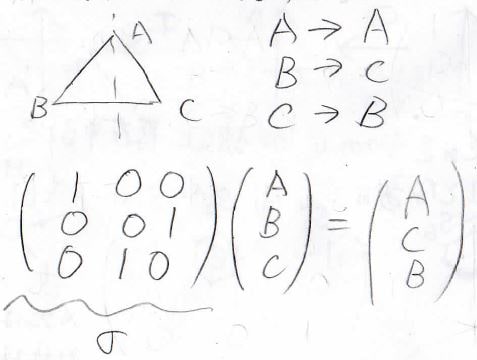
対称操作の関係式
そして、行列として表現すると、かけ算ができるようになります。
そこで、対称操作間で成り立つ関係式をまとめます。
まず、\(n\)が\(m\)という約数をもつとき、\(C_n\)軸は\(C_m\)にもなります。
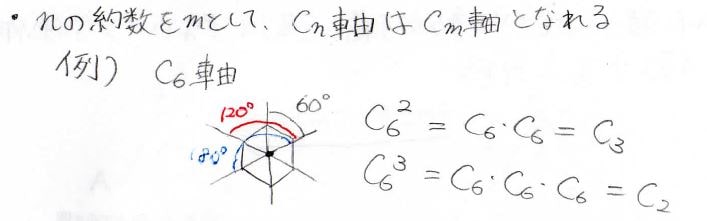
例えばベンゼンの場合、\(C_6\)軸を持っており、つまり\(60^\circ\)回転させても、元の形と同じになるということです。
この場合、6回回転を2回続けて行う操作、これも対称操作になります。
\(60^\circ\)回転を2回行うのは、つまり\(120^\circ\)回転させるということなので、3回回転になります。
\(C_6\)の操作を2回続けて行うことを\(C_6^2\)として表すとすると、これが\(C_3\)になります。
また、\(C_6^3=C_2\)にもなります。
そして、\(C_n\)を\(n\)回繰り返すと一周してもとに戻る、すなわちこれは恒等操作になるため、\(C_n^n=E\)となります。
続いての関係は、鏡映と反転は2回行うと元に戻るということです。
つまり、\(\sigma^2=E\)で、\(i^2=E\)となります。
続いて、回映は回転と鏡映の積になります。
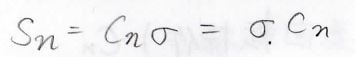
そして、対称操作は可換なので、どっちを先に行っても構いません。
最後、\(S_n^n\)は\(E\)もしくは\(\sigma\)になります。
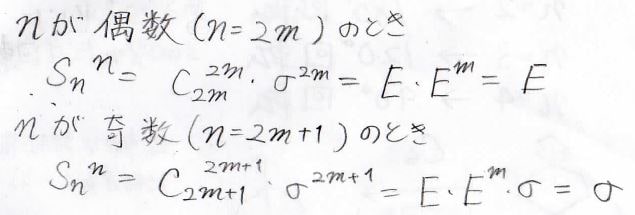
どちらになるかは、\(n\)が奇数か偶数かで決まります。
練習問題
今回の話は以上なので、練習問題をやってみます。
アンモニア分子がもつ対称操作をすべて挙げるとどうなるでしょうか？
次に孤立電子対の軌道が向いている方向を軸とすると、これは3回回転軸になります。
そして、\(120^\circ\)回して対称であれば、\(240^\circ\)回しても対称でもあるので、\(C_3^2\)も対称操作になります。
最後、窒素原子と水素原子を結ぶ直線と主軸をどちらも含む鏡映面\(\sigma_\rm{v}\)を3つ考えることができます。
したがって答えは、\(E\)、\(C_3\)、\(C_3^2\)、\(\sigma_\rm{v}\)、\(\sigma_\rm{v}’\)、\(\sigma_\rm{v}^”\)の6つです。
ちなみに、\(C_3\)と\(C_3^2\)、\(\sigma_\rm{v}\)と\(\sigma_\rm{v}’\)と\(\sigma_\rm{v}^”\)はまとめて類と呼びます。
同じ類に含まれる操作は互いに、その群の中で相似変換することが可能です。
詳しくは、こちらの記事で解説しています。
まとめ
はい、お話は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitterかお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました！
