こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマは、こちら!
動画はこちら↓
動画で使ったシートはこちら(Hess)
それでは内容に入っていきます!
状態量(状態関数)
まず、改めて状態量(状態関数)という言葉を説明しておきます。
これは、変化の経路によらず、そのときのほかの状態量によって決まる量のことです。
例えば、絶対温度\(\displaystyle T\)が決まれば理想気体の内部エネルギー\(\displaystyle U\)は自動的に決まります。

ここで、\(\displaystyle n\)は物質量、\(\displaystyle R\)は気体定数です。
これに対して、仕事や熱は変化の仕方を表す量であり、温度や圧力、体積だけでは一意的に決まらず、経路関数と言います。
そして、エンタルピー\(\displaystyle H\)の定義は\(H=U+pV\)ですが、内部エネルギー、圧力、体積はすべて状態量であるため、エンタルピーも状態量になります。

理想気体の状態方程式\(\displaystyle pV=nRT\)より、\(\displaystyle H=\frac{5}{2}RT\)と書けます。
ここで、\(\displaystyle p\)は圧力、\(\displaystyle V\)は体積です。
ヘスの法則
したがって、\(\displaystyle \rm{A}\)と\(\displaystyle \rm{B}\)から\(\displaystyle \rm{C}\)と\(\displaystyle \rm{D}\)ができる反応におけるエンタルピー変化は、下のようにいったん\(\displaystyle \rm{A’}\)と\(\displaystyle \rm{B’}\)を経由しても変わらないことになります。
![]()
![]()
この法則は、ヘスの法則と言います。
これにより、その反応が実際に起こっているかどうかに関わらず、複数の反応エンタルピーの値から、全体の反応エンタルピーを求めることができます。
中でも、それぞれの化学種の生成エンタルピー\(\Delta_\rm{f}\)\(H\)から全体の反応エンタルピーを求めるのが簡単です。
こちらはメタンの生成反応です。
![]()
ここでは、炭素なら黒鉛、水素なら水素ガスというように、その状態における最も安定な単体を基準に生成物のエンタルピーを考えます。

そのため、これら基準物質の生成エンタルピーは\(0\)です。
そして、実際に生成エンタルピーを使って反応エンタルピーを表すと、下のようになります。
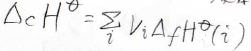
ここでは、エタンの燃焼反応を例にしています。
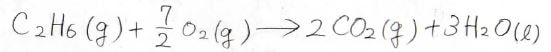

以前の記事で、それぞれの標準エンタルピーから標準反応エンタルピーを求める方法をお話ししましたが、それとほとんど同じです。
詳しくはこちらを参照してください。

反応系の係数にマイナスをつけるという化学量数\(\nu_i\)で表せます。
ただし、基準物質である酸素ガスの生成エンタルピーは\(0\)になるので、書かなくてもよいというところだけ違います。
反応エンタルピーの温度依存性
次に、ここまでは標準状態だけしか考えていなかったので、今度は温度を変化させることを考えてみましょう。
ここからの話で、圧力は標準圧力で一定であるとします。
任意の温度\(T\)における反応エンタルピーは、標準温度での値と、そこから温度変化したことによる差分との和で書けます。
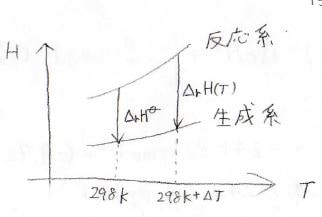
圧力一定下におけるエンタルピーの微小変化\(\rm{d}\)\(H\)は定圧熱容量\(C_p\)と温度の微小変化\(\rm{d}\)\(T\)の積になるので、反応系と生成系の定圧熱容量の差によって、反応エンタルピーの温度依存性が決まります。
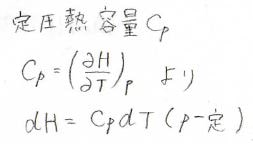
温度の変化量\(\Delta T\)が小さく、熱容量の温度依存性を無視できる場合には、それぞれの化学種について、このような式が成り立ちます。
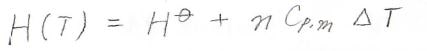
ここで、\(C_{p,\rm{m}}\)はモル定圧熱容量です。
そして、このときの反応エンタルピー\(\Delta_\rm{r}\)\(H\)は、熱容量の差を使ってこのように表すことができます。
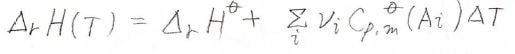
ここで、\(\rm{A}_i\)は化学種の種類を表しています。
それで、熱容量に温度依存性がある場合には、下のように積分の式になります。

これら反応エンタルピーの温度依存性を熱容量差で表した関係は、反応熱のキルヒホッフの法則と呼ばれます。
また、上の積分の式を微分形に変形すると、下のように表現することもできます。
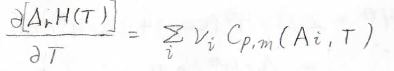
実際の計算例
最後に、実際に反応エンタルピーの温度変化を考えてみましょう。
ここでは、\(110^\circ \rm{C}\)における水素ガスの燃焼を例にしています。
![]()
標準温度\(25^\circ \rm{C}\)、標準圧力\(1\ \rm{bar}\)のとき、それぞれの標準モル定圧熱容量と全体の標準燃焼エンタルピーが、下記の値になったとします。
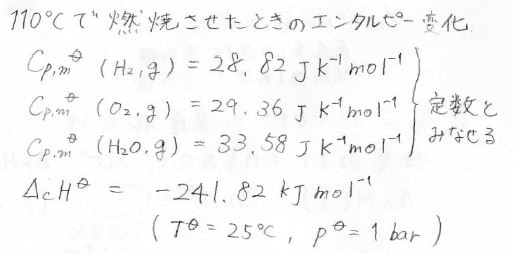
そして、熱容量の温度変化は無視できるものとします。
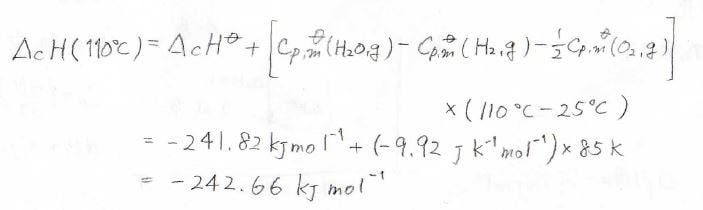
このとき、反応系と生成系の熱容量差を用いて、\(\Delta_\rm{c}\)\(H(110^\circ \rm{C}\)\()=-242.66\ \rm{kJ \ mol^{-1}}\)と計算できます。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!