こんにちは!
今回も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら!
動画で使ったシートはこちら(anharmonic oscillator)
非調和振動子とは
まず、ばねで繋がった2原子分子を考えてみましょう。

このばねが振動するわけですが、原子は質点ではなく大きさをもっているので、ばねが縮んだときに立体的な反発が生まれます。
そのため、ばねが短いときには、調和振動子のポテンシャルより実際のポテンシャルのほうが大きいことになります。
そして、ばねの長さが無限大のときには、それはもはや結合が解離しているため、ばねの復元力ははたらかず、ポテンシャルは\(0\)になります。
つまり、結合長が長い領域では、実際のポテンシャルエネルギーは調和振動子より小さくなります。
それを考慮したのがこちらの図になります。

点線が調和振動子で、実線が実際のポテンシャルです。
調和振動子であれば、平衡核間距離\(r_\rm{e}\)を中心に左右対称となるのですが、実際の系では左が上がって右が下がっているので左右非対称となります。
この調和振動子からずれた分をハミルトニアンの摂動としてエネルギーを求めてみようというのが今回の趣旨です。
ちなみに、このポテンシャル図はあくまでわかりやすくしたものであり、実際のポテンシャルはよりシャープな谷の形になっているのが普通なので、知っておいてください。
ハミルトニアンの摂動
ここからは、摂動の形を考えていきます。
とりあえず、ポテンシャルをマクローリン展開の形で書いてみましょう。

マクローリン展開についてはこちらの記事で解説しています。

ここで、ばねの長さが平衡核間距離に近い場合は、立体反発や結合の解離が関係しないので、ほとんど調和振動子であると考えることができます。
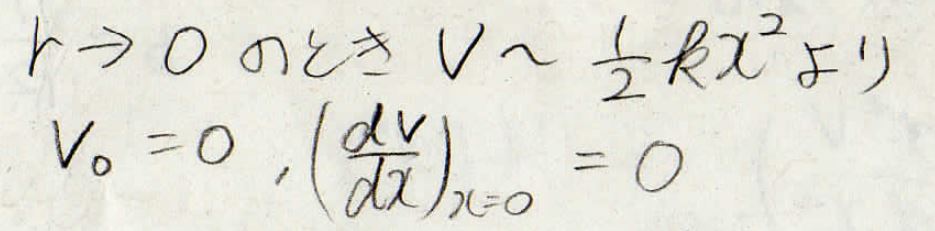
そのため0次、1次の項が\(0\)になるとしておきます。
2次の項は\(\displaystyle \frac{1}{2}kx^2\)としておいて、今回は4次の項までを考えることにします。
その係数は、\(a\)と\(b\)にしておきます。
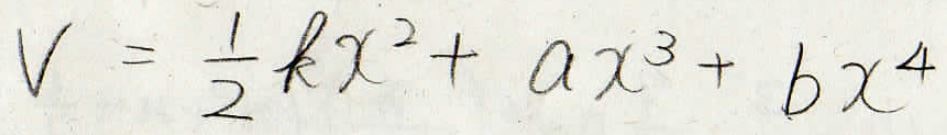
このポテンシャルを使って、エネルギーの変化分を考えていきます。
エネルギーの補正項
一次摂動エネルギー
前々回の記事で、エネルギーの補正項は補正前の波動関数から出せるということをお話ししたので、とりあえず調和振動子の波動関数を思い出してみます。
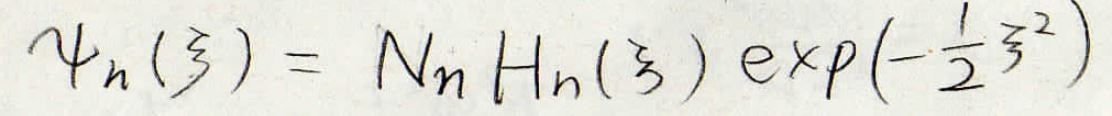
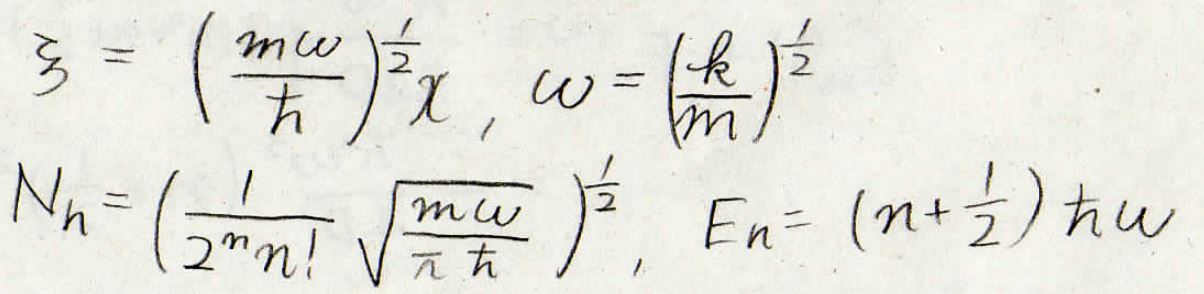
ここで、\(N_n\)は規格化定数です。
\(H_n\)はエルミート多項式といって、下の形で与えられました。
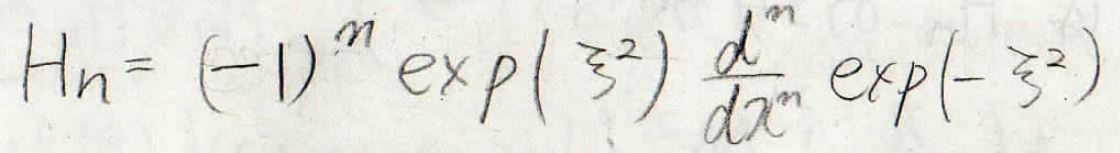
実は、エルミート多項式にはある漸化式が成り立つことが知られています。
詳しい導出は割愛するので、気になる方だけ「エルミート多項式 漸化式」で検索していただきたいのですが、\(\xi H_n=nH_{n-1}+\frac{1}{2}H_{n+1}\)という式が成り立ちます。
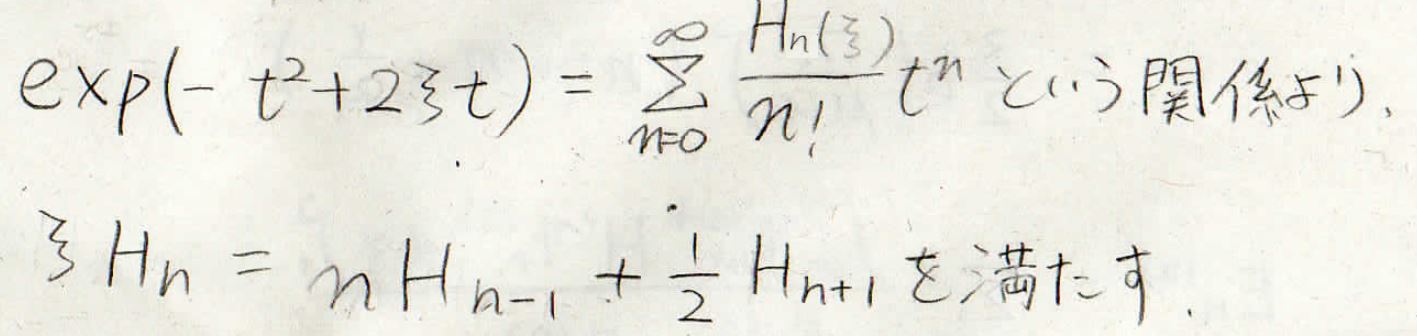
この式を使うと計算が簡単になるので、最初に少し変形をしていきます。
まず、この式の\(H_{n-1}\)と\(H_{n+1}\)をこの漸化式から書き換えます。
そして\(\xi H_n\)を表すと、下の式になります。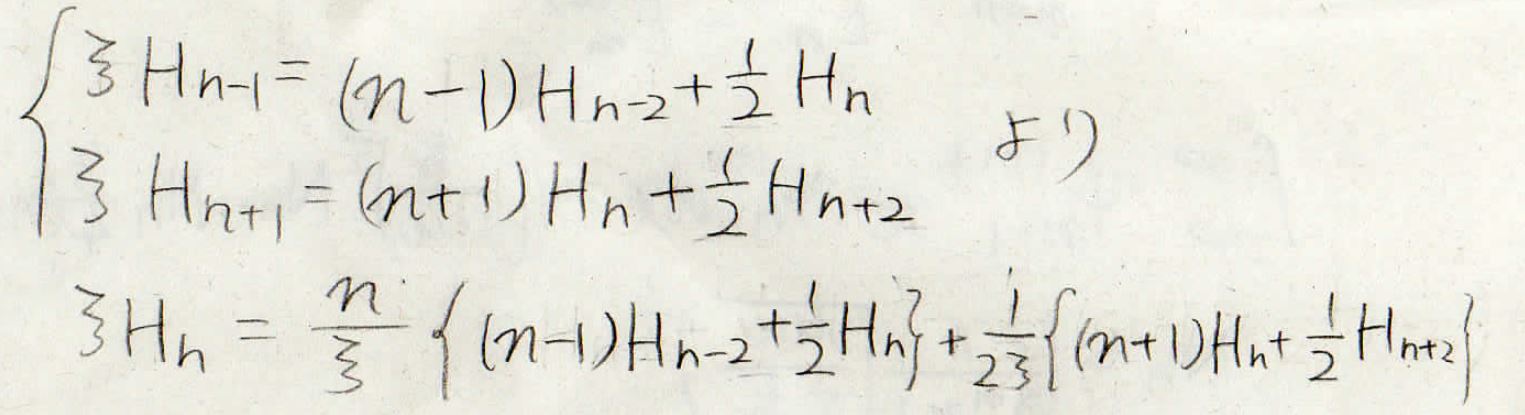
両辺に\(\xi\)をかけると\(\xi ^2H_n\)を\(H_{n-2}\)と\(H_n\)と\(H_{n+2}\)で表した式になります。
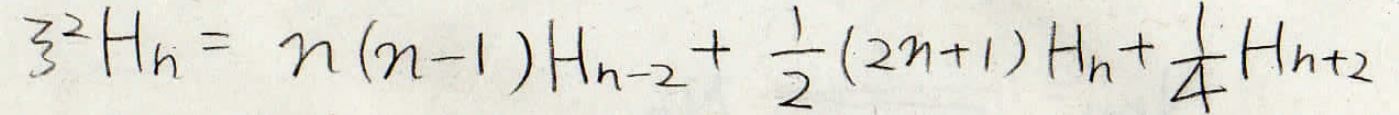
そして、さらに右辺の\(H_{n-2}\)、\(H_n\)、\(H_{n+2}\)をすべて書き換えて、また両辺に\(\xi\)をかけたものがこの式になります。
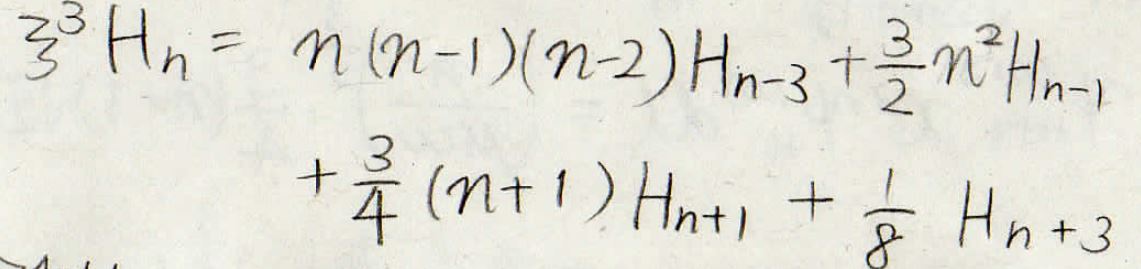
今度は\(\xi ^3H_n\)を\(H_{n-3}\)、\(H_{n-1}\)、\(H_{n+1}\)、\(H_{n+3}\)で表すことができました。
これをもう一度行うと\(\xi ^4H_n\)を\(H_{n-4}\)、\(H_{n-2}\)、\(H_n\)、\(H_{n+2}\)、\(H_{n+4}\)で表せるということになります。
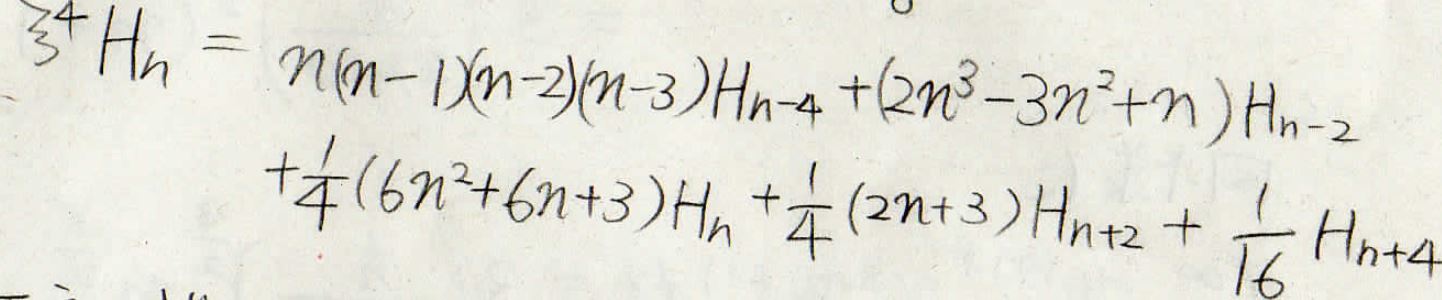
以上の関係式から、エネルギーの補正項を考えると、次のようになります。
まず、一次の補正項は下記のようになります。
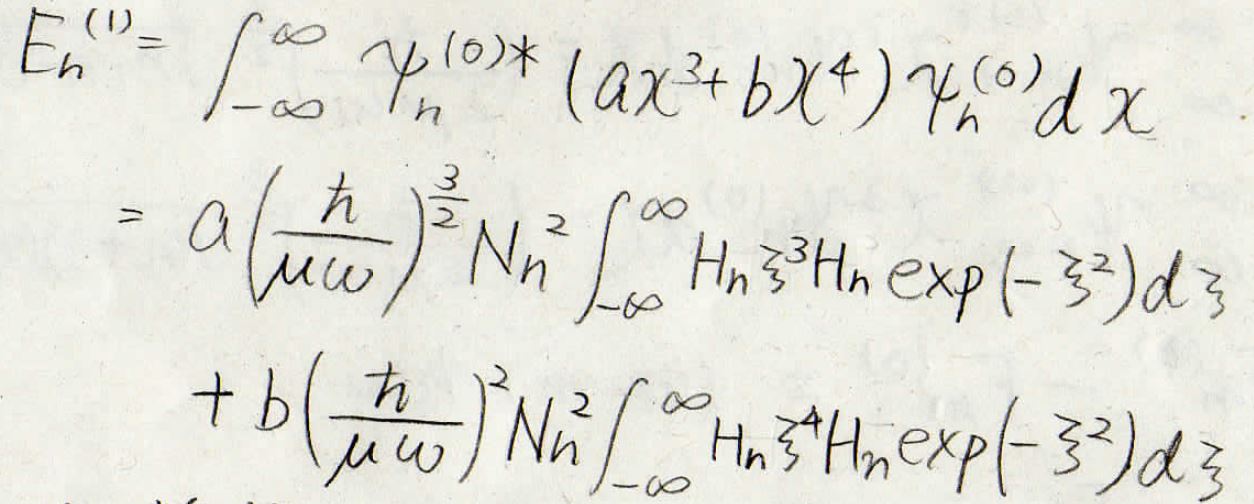
ここで、\(\mu\)は換算質量です。
エルミート多項式が直交性を満たすことから、\(0\)になる項がわかります。
一次摂動エネルギーについてはこちらをご覧ください。

換算質量についてはこちらをご覧ください。

まず、\(\xi ^3H_n\)について、先ほどの漸化式から求めたものを見ると、\(H_n\)がないため、直交性よりすべて消えてしまうことになります。
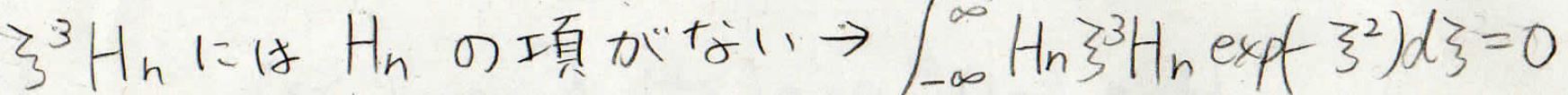
よって、\(\xi ^4\)部分だけが残ることになり、エネルギーの補正項をこのように求めることができます。

二次摂動エネルギー
同様に2次の補正項も考えると、\(\xi ^3\)だけが残ってきます。
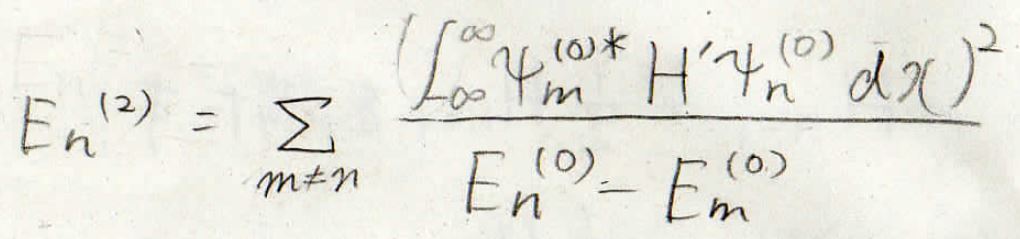
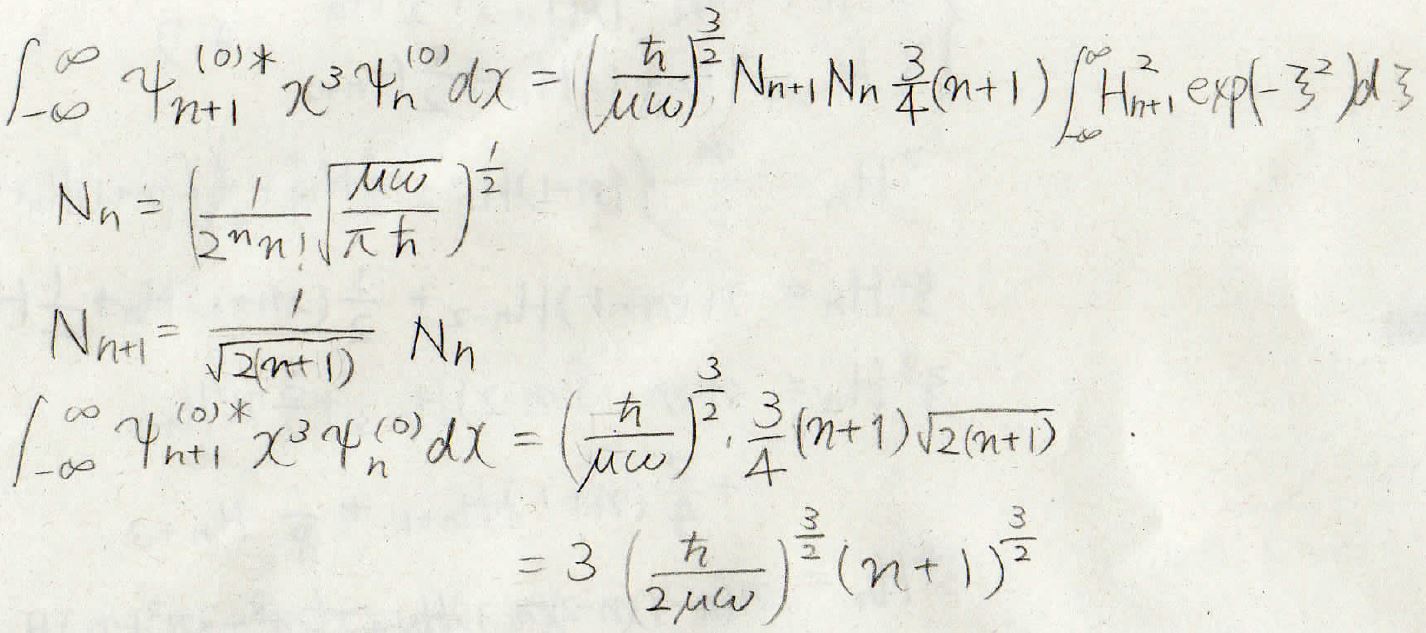
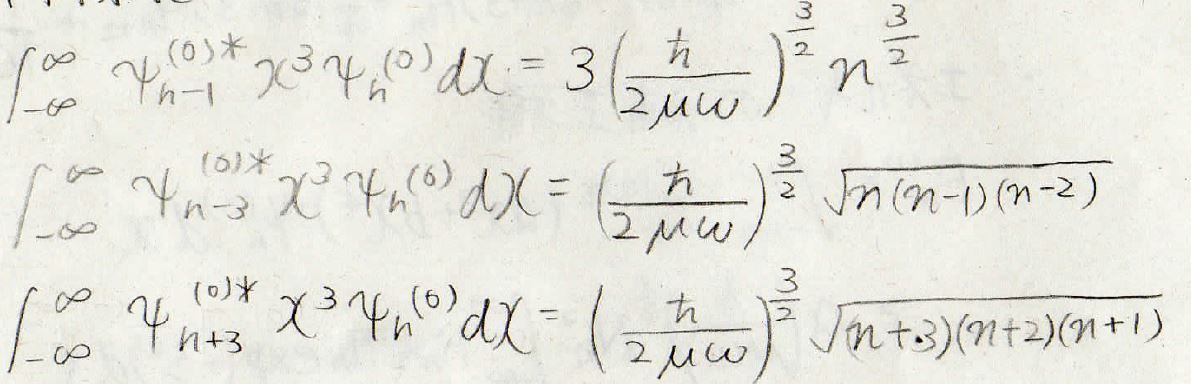

最終的には、このようなエネルギーの値が得られます。
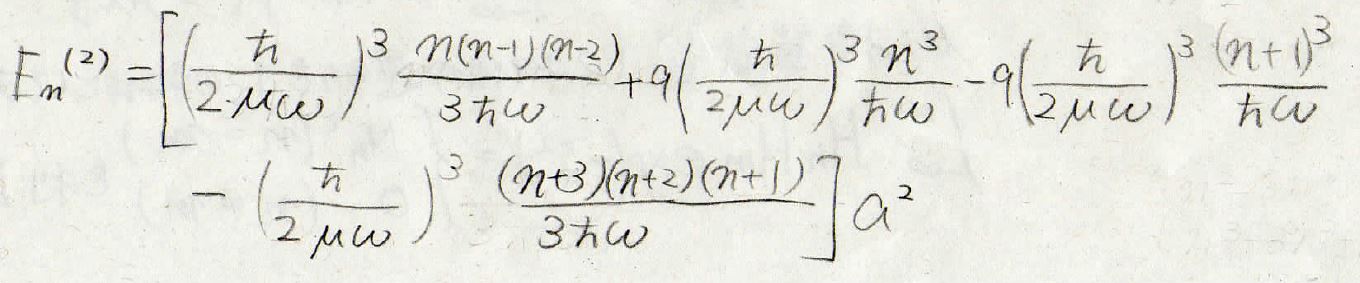
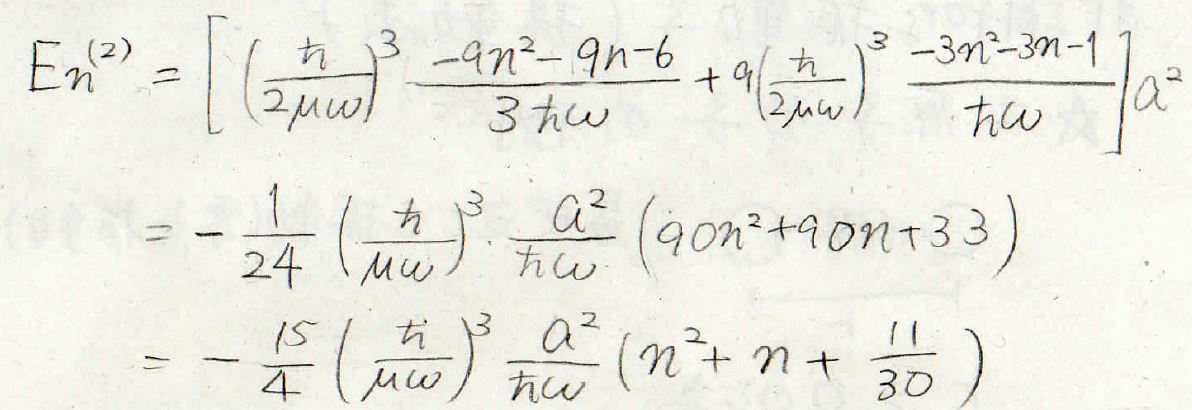
モースポテンシャル
最後に、非調和な振動ポテンシャルの例としてモースポテンシャルと呼ばれる式を考えてみましょう。
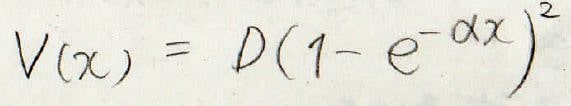
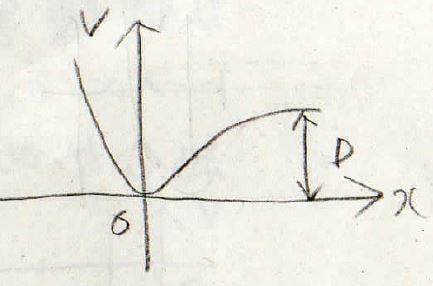
ここで、\(D\)はポテンシャルの最小値から解離したところのポテンシャルまでの差を表しており、\(\alpha\)はカーブの曲がり具合を表すパラメータです。
このポテンシャルをマクローリン展開した際には、0次と1次の項は\(0\)になっています。
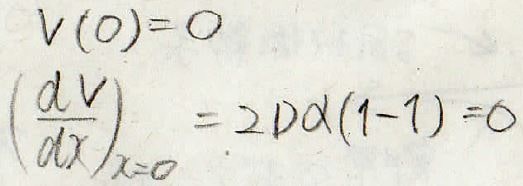
そして、2次の項の係数の関係より\(\alpha\)をこのように表すことができます。
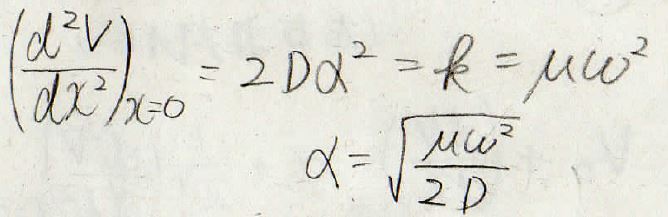
3次、4次の係数は、導関数から下のように表せるため、\(a\)と\(b\)を求めることができます。
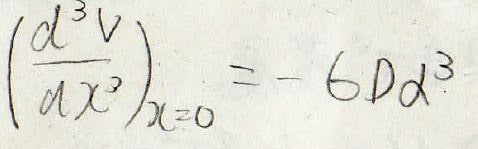
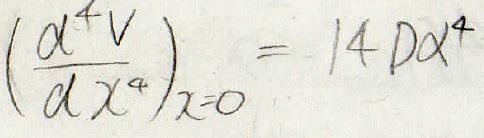
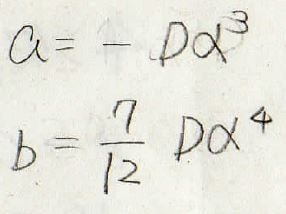
これをエネルギーの補正項に入れることで、数値として表すことができるようになります。
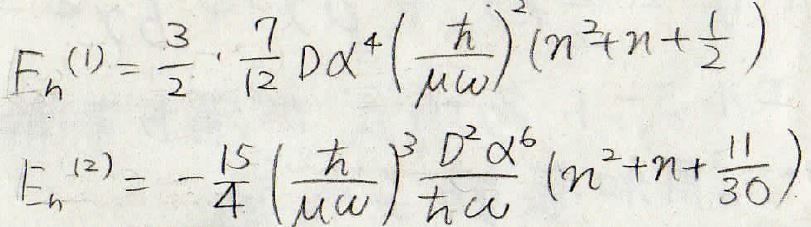
そしてエネルギーを2次まで補正した際のエネルギーの変化分は、\(\displaystyle -\frac{\hbar ^2\omega ^2}{4D}(n+\frac{1}{2})^2\)ということになります。
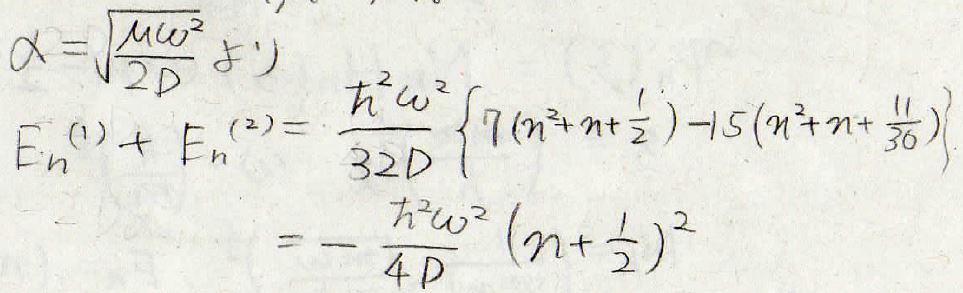
調和振動子のエネルギー準位は等間隔でしたが、摂動を考えると\(n\)が大きくなるにつれて、だんだん間隔が小さくなっていくことをこの式は示しています。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




