こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(statistical representations)
それでは内容に入っていきます!
分配関数とカノニカル分布
まずは、ボルツマン分布導出の記事でお話しした、分配関数とカノニカル分布の話を復習します。
こちらの記事です。

今回考えるモデルとパラメータは、次のとおりです。
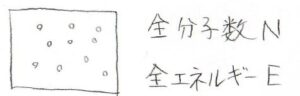
\(N\)個の気体分子があるとして、その全体のエネルギーを\(E\)とします。
それぞれの分子は離散的なエネルギーをとることにして、その値を\(\varepsilon\)で表します。

基底状態のエネルギーが\(\varepsilon_0\)、第一励起状態が\(\varepsilon_1\)、・・・と添字を付けていきます。
また、各状態にある分子の個数を\(N_0\)、\(N_1\)、\(\displaystyle \cdots\)としていきます。
そして、各状態の縮退度も\(g_0\)、\(g_1\)、\(\displaystyle \cdots\)としておきます。
また、今回は式を簡単にするため、基底状態のエネルギー\(\varepsilon_0=0\)として、ここを基準とします。
基底状態の縮退がないとき、ボルツマン分布により、\(\displaystyle \frac{N_i}{N_0}\)はこのように書けます。
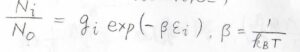
ここで、\(k_\rm{B}\)はボルツマン定数、\(T\)は絶対温度です。
そして、分母を全体の分子数\(N\)とすると、\(i\)番目の状態にある分子の割合になります。
いま、これを存在確率\(P_i\)と呼ぶことにします。
分子と分母を\(N_0\)で割ると、下のように表せることがわかります。
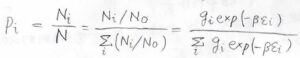
この分布のことをカノニカル分布、または正準分布と呼びます。
意味としては、温度一定の閉鎖系、すなわち外界と物質のやり取りはなく、エネルギーのやり取りだけをするという系での存在確率を表します。
このカノニカル分布の分母、つまり\(\displaystyle \frac{N}{N_0}\)は分配関数と言って、ここでは\(q\)と表すことにします。
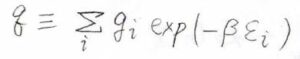
全体の分子数\(N\)は固定ですが、温度によって基底状態の分子数\(N_0\)が変化するため、\(q\)は温度の関数であることになります。

温度が絶対零度近傍のときには、基底状態にほぼすべての分子があることになり、分配関数は\(1\)に近い値となります。
温度がとても高いときには、基底状態にある分子の存在確率が小さくなり、分配関数もとても大きな値となります。
そして、分子1個あたりの平均エネルギーを\(\langle \varepsilon\rangle\)とすると、これは全体のエネルギー\(E\)を全分子数\(N\)で割った値となるわけですが、\(\varepsilon_i \exp{(-\beta \varepsilon_i)}\)の部分は\(-\exp{(-\beta \varepsilon_i)}\)を\(\beta\)について偏微分した値と考えることができます。

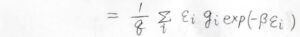
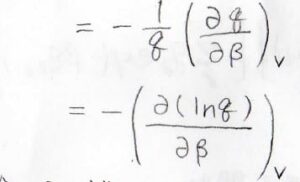
したがって、\(\displaystyle \langle \varepsilon\rangle=-\frac{1}{q}(\frac{\partial q}{\partial \beta})_V\)となります。
さらには、\(\displaystyle \frac{1}{q}\)の部分も\(\ln{q}\)を\(q\)について微分したものと考えられるので、合成関数の微分の考え方で\(\displaystyle \langle \varepsilon\rangle=-[\frac{\partial (\ln{q})}{\partial \beta}]_V\)となります。
全体のエネルギー\(E\)は、これに分子数\(N\)をかけたものになります。
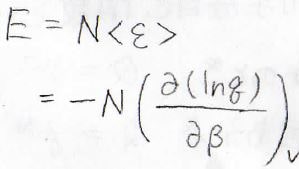
ここで、偏微分の際に固定している変数は、体積\(V\)です。
一次元井戸型ポテンシャルのエネルギー準位の式を思い出してみると、これは井戸の幅\(L\)の\(2\)乗に反比例しているので、三次元になると空間の体積によってエネルギー準位が変化することになります。

詳しくは、こちらを参照ください。

\(\varepsilon_i\)を定数と考えて\(\beta\)について偏微分するために、体積を固定しているという訳です。
そして、\(\displaystyle \beta=\frac{1}{k_\rm{B}\mathit{T}}\)より、温度についての偏微分という形に変形させることもできます。
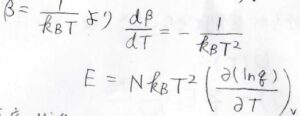
すると、\(E=Nk_\rm{B}\)\(\displaystyle T^2[\frac{\partial (\ln{q})}{\partial T}]_V\)となります。
いま、基底状態のエネルギーを基準として\(0\)にしていたため、この値は、零点エネルギーを基準とした内部エネルギー\(U\)の値に等しくなります。
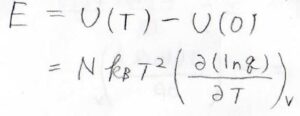
分子分配関数と集合分配関数
続いて、分子分配関数と集合分配関数という考え方について、お話ししていきます。
閉鎖系で、2種類の気体分子\(\rm{A}\)と\(\rm{B}\)が\(1\)個ずつ閉じ込められていたとします。
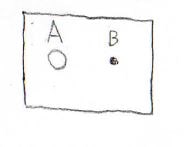
それぞれのエネルギー準位は\(\varepsilon_\rm{A}\)、\(\varepsilon_\rm{B}\)と表し、異なる値でもよいものとします。
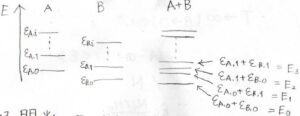
ここで、系全体のエネルギー準位を考えてみると、もっとも低いのが\(\varepsilon_\rm{A, 0}\)\(+\varepsilon_\rm{B, 0}\)で、そこから\(\varepsilon_\rm{A, 0}\)\(+\varepsilon_\rm{B, 1}\)、\(\varepsilon_\rm{A, 1}\)\(+\varepsilon_\rm{B, 0}\)、\(\displaystyle \cdots\)と高くなっていきます。
もちろん、この順番は一例にすぎず、基底状態以外の値はデタラメです。
この系全体のエネルギーに関しては、低いものから順に\(E_0\)、\(E_1\)、・・・というように表すことにします。
すると、系全体についての分配関数\(Q\)は、下のように書けます。
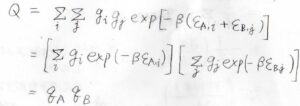
指数の和の形をかけ算に変形すると、結局、分子\(\rm{A}\)の分配関数\(q_\rm{A}\)と分子\(\rm{B}\)の分配関数\(q_\rm{B}\)の積となります。
この系全体についての分配関数のことを集合分配関数、\(q_\rm{A}\)や\(q_\rm{B}\)のことを分子分配関数と言って区別します。
ここで仮に、\(\rm{A}\)と\(\rm{B}\)が同じ分子であった場合には、\(Q=q^2\)となります。
さらに、その分子の個数が\(2\)個から\(N\)個になった場合は、\(Q=q^N\)となります。
そこから、分子が自由に飛び回っていて個々の分子を区別できない場合などは、場合の数と同じ考え方で、\(\displaystyle Q=\frac{q^N}{N!}\)となります。
先ほどと同様に集合分配関数から内部エネルギーを求めても、\(\displaystyle Q=\frac{q^N}{N!}\)を代入すると、まったく同じ答えが出てきます。
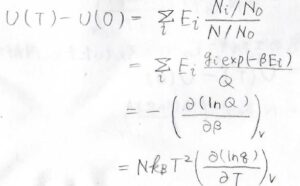
分配関数を用いた熱力学量の表現
ここからは、内部エネルギー以外の熱力学量も分配関数を使って表せるかということを考えていきます。
まずは、エントロピーからいきます。
状態\(i\)にある分子の存在確率を\(P_i\)とすると、内部エネルギー\(\displaystyle U=\sum_i E_iP_i\)という期待値の形で書くことができます。
これを使うと、内部エネルギーの全微分は、下のように書けます。

ここで、\(P_i\)が変化するのは温度が変化することに対応しているので、第一項は可逆系において系へ与えられた熱量に相当します。
熱力学第一法則より、第二項は可逆系において系へなされた仕事だということになります。
系が可逆であることを仮定すると、エントロピーの定義\(\rm{d}\)\(\displaystyle S=\frac{\rm{d’}\mathit{q}}{T}\)より、\(\rm{d}\)\(\displaystyle S=\frac{1}{T}\sum_i E_i \rm{d}\)\(P_i\)となります。
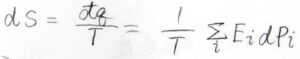
ここで、\(P_i\)はすでに求められており、\(Q\)と\(P_i\)を使うことで\(E_i\)を消去することができます。
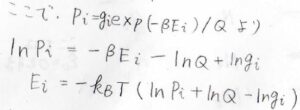
さらに、\(P_i\)の和が必ず\(1\)となることを利用すると、\(\displaystyle \sum_i \rm{d}\)\(P_i=0\)となるため、これを使って変形していきます。
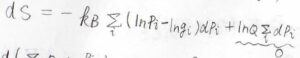
すると、\(\rm{d}\)\(S=\rm{d}\)\([-k_\rm{B}\)\(\displaystyle \sum_i P_i\ln{(\frac{P_i}{g_i})}]\)という式が出てきます。
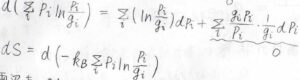
両辺を温度について\(0\ \rm{K}\)から\(T\)まで定積分すると、熱力学第三法則に従って\(S(0)=0\)となる場合には、素片を表す\(\rm{d}\)が消えた式になります。
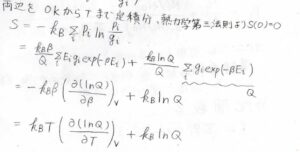
\(P_i\)はすでにわかっているので、それを代入すると、再び\(\beta\)についての偏微分で\(E_i\)を消すことができるので、結局\(Q\)と\(\beta\)だけが残ることになります。
そして、\(\beta\)に\(\displaystyle \frac{1}{k_\rm{B}\mathit{T}}\)を代入すると、最終的に\(S=k_\rm{B}\)\(\displaystyle T[\frac{\partial (\ln{Q})}{\partial T}]_V+k_\rm{B}\)\( \ln{Q}\)という式が出てきます。
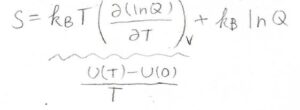
ここで、第一項は内部エネルギー\(U\)を絶対温度\(T\)で割った値に等しくなります。
これを利用すると、ヘルムホルツエネルギーが簡単に求められます。
ヘルムホルツエネルギー\(A\)の定義\(U-TS\)より、\(S\)に上の式を代入すると、\(U\)が消去されて、\(A=-k_\rm{B}\)\(T\ln{Q}\)とエントロピーの第二項だけが残る形になります。
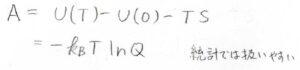
ヘルムホルツエネルギーを実験的に扱う場合には、温度と体積を一定にする必要があり、それはギブズエネルギーの温度と圧力一定という条件よりも作り出すのが難しく、なかなか使いにくいです。
しかし、理論を扱う場合は話が変わってきて、統計学的にはヘルムホルツエネルギーがいちばんシンプルな式になるので、とても扱いやすくなります。
エンタルピーやギブズエネルギーの導出も、ヘルムホルツエネルギーの式から始めるのが簡単です。
まずエンタルピーについては、変数を温度と体積、そして分子に固有の分配関数としているので、これらで圧力\(p\)を表します。
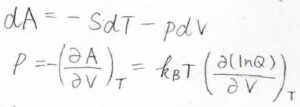
ヘルムホルツエネルギーについての基本式より、\(\displaystyle p=-(\frac{\partial A}{\partial V})_T\)なので、結局\(p=k_\rm{B}\)\(\displaystyle T[\frac{\partial (\ln{Q})}{\partial V}]_T\)となります。
エンタルピー\(H\)の定義\(U+pV\)より、\(p\)に上の式を代入して、最終的に\(H=k_\rm{B}\)\(\displaystyle T^2[\frac{\partial [\ln{Q})}{\partial T}]_V+k_\rm{B}\)\(\displaystyle TV[\frac{\partial (\ln{q})}{\partial V}]_T\)という式が得られます。
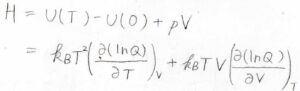
そして、ギブズエネルギー\(G\)の定義\(A+pV\)より、同様に\(G=-k_\rm{B}\)\(T\ln{Q}+k_\rm{B}\)\(\displaystyle TV[\frac{\partial (\ln{Q})}{\partial V}]_T\)となります。
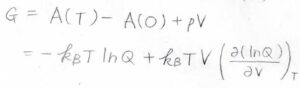
練習問題
最後に、練習問題をやって終わります。
(1)定積熱容量\(C_V\)と定積熱容量\(C_p\)を\(T\)、\(V\)、\(p\)、\(Q\)を使って表すと、どうなるでしょうか?
(2)温度と体積一定条件下でゴムを引っ張ったときに、その張力\(f\)を\(T\)、\(Q\)、\(V\)、\(L\)を使って表してください。
ただし、\(L\)は伸長方向についてのゴムの長さを指します。

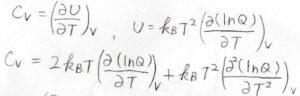
内部エネルギー\(U=k_\rm{B}\)\(\displaystyle T^2[\frac{\partial (\ln{Q})}{\partial T}]_V\)であることから、関数の積の微分を考えていきます。
すると結局、\(C_V=2k_\rm{B}\)\(\displaystyle T[\frac{\partial (\ln{Q})}{\partial T}]_V+k_\rm{B}\)\(\displaystyle T^2[\frac{\partial^2 (\ln{Q})}{\partial T^2}]_V\)となります。
そして、\(C_p\)の定義\(\displaystyle (\frac{\partial H}{\partial T})_p\)より、\(C_p=2k_\rm{B}\)\(\displaystyle T[\frac{\partial (\ln{Q})}{\partial T}]_V+k_\rm{B}\)\(\displaystyle T^2\{\frac{\partial}{\partial T}[\frac{\partial (\ln{Q})}{\partial T}]_V\}_p+p(\displaystyle \frac{\partial V}{\partial T})_p\)となります。

問題では、\(T\)、\(V\)、\(p\)、\(Q\)を使って表せということだったので、ここまでで構いませんが、\(p\)は\(T\)、\(V\)、\(Q\)の関数になっていて独立ではないので、消去することもできます。
そのときには、オイラーの連鎖式を使うことになります。
かなり複雑になるので、やってみたい方だけやってみてください。
そして(2)では、まず、ゴムの伸長によって与えられた仕事の分だけ内部エネルギーが上昇することを考えなければなりません。
内部エネルギーの微小変化\(\rm{d}\)\(U\)は\(f\rm{d}\)\(L\)だけ変化することになるため、ヘルムホルツエネルギーの微小変化\(\rm{d}\)\(A\)にも\(f\rm{d}\)\(L\)という項が付きます。

この基本式を全微分とみなすと、\(\displaystyle f=(\frac{\partial A}{\partial L})_{T, V}\)より、\(f=-k_\rm{B}\)\(\displaystyle T[\frac{\partial (\ln{Q})}{\partial L}]_{T, V}\)となります。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!