こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(microwave spectroscopy)
それでは内容に入っていきます!
純回転遷移に関係する光の波長
三フッ化窒素やアンモニア、塩化水素などといった比較的小さな分子の回転定数\(\tilde{B}\)は、\(0.1\sim 10\ \rm{cm}\)\(^{-1}\)の範囲に収まることが多く、吸収もしくは放出される光の波長としては、\(0.1\sim 10\ \rm{cm}\)の範囲になります。
回転定数については、こちらを参照してください。

これは、遠赤外からマイクロ波の波長領域に相当します。
したがって、小さな分子の振動や電子状態の遷移を伴わない純粋な回転状態の遷移を見るためには、マイクロ波を使うことになります。
純回転遷移の選択律
ただし、すべての分子について、純回転遷移を観測できるわけではありません。
選択概律
マイクロ波は電場と磁場の波であり、これらと分子の回転運動が干渉するためには、分子全体が磁石のようになっていなければいけません。

このようなルールのことは選択律と言います。
ここでは、量子力学を使っていない大雑把な選択律という意味で、選択概律と書いています。
この選択概律にあてはまる分子を活性である、あてはまらない分子を不活性であると言います。
極性分子である水やアンモニア、塩化水素などは、純回転活性となります。
対して、極性をもたない単原子分子や等核二原子分子、二酸化炭素やアセチレン、メタンなどは純回転不活性です。
個別選択律
そして、選択概律に当てはまる活性な分子でも、すべての純回転遷移が起こるわけではありません。
回転量子数変化\(\Delta J\)が、光の吸収で\(+1\)、放出では\(-1\)となる遷移しか起こりません。
さらに、実験室内に固定された軸を考えると、この軸方向についての角運動量成分も量子化されます。

その量子数を\(M_J\)としたとき、\(M_J\)の変化が\(-1\)、\(0\)、\(+1\)のいずれかとなる遷移しか起こりません。
それぞれの分子で主軸や回転軸の方向が違いますが、たとえば入射光や透過光の進行方向は、測定装置のみに依存します。
実験室内に固定された軸とは、こういったものを指していると考えてください。
この選択律は、個別選択律と言います。
ここからは、個別選択律がどのような理屈からくるものなのか説明します。
まず、ボルン-オッペンハイマー近似を適用して、分子全体の波動関数\(\psi_\rm{total}\)を中心の並進運動、分子全体の振動運動、回転運動、電子状態それぞれの波動関数の積として書きます。

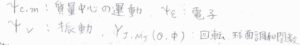
回転運動については、球面調和関数\(Y_{J, M_J}(\theta, \phi)\)が波動関数になります。
ここで、遷移に伴って生じた電荷の偏りの変化を表す遷移双極子モーメントを考えます。
状態\(\rm{i}\)から状態\(\rm{f}\)への遷移に対応する遷移双極子モーメントを\(\boldsymbol{\mu}_\rm{fi}\)とすると、それはこちらの形で書けます。
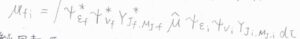
\(\boldsymbol{\mu}_\rm{fi}=\boldsymbol{0}\)とならない遷移を許容遷移と言って、実験ではこの遷移が主に観測されることになります。
\(\boldsymbol{\mu}_\rm{fi}=\boldsymbol{0}\)となる遷移は、禁制遷移と呼ばれ、理論上起こらない遷移だと判定できます。
ただ実際には、低い確率ながら禁制遷移が観測されることがあり、これは四極子モーメントとしての値をもっていたり、他の電子状態の寄与があったりなどが原因として考えられています。
純回転遷移では、振動の量子数と電子の量子数が変化しないので、状態\(\rm{i}\)における永久双極子モーメント\(\boldsymbol{\mu}_\rm{i}\)を使うと、\(\boldsymbol{\mu}_\rm{fi}\)\(\displaystyle =\int Y_{J_\rm{f}, \mathit{M}_{\mathit{J}_\rm{f}}}^\ast \boldsymbol{\mu}_\rm{i}\)\( Y_{J_\rm{i}, \mathit{M}_{\mathit{J}_\rm{i}}} \rm{d}\)\(\tau\)となります。
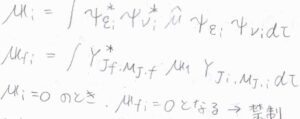
\(\boldsymbol{\mu}_\rm{i}\)\(=\boldsymbol{0}\)のとき、\(\boldsymbol{\mu}_\rm{fi}\)\(=\boldsymbol{0}\)となることから、永久双極子モーメントをもたない分子の純回転遷移は、すべて禁制であることになります。
これは、古典的な電磁気学から予想した選択概律と矛盾しません。
ここからは、球面調和関数の性質を利用したテクニックを使います。
任意のベクトル\(\boldsymbol{\mu}_\rm{l}\)について、その\(x\)、\(y\)、\(z\)成分を極座標で表します。
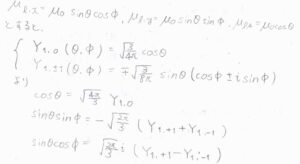
\(\boldsymbol{\mu}_\rm{l}\)の大きさを\(\mu_0\)としています。
そして、球面調和関数\(\displaystyle Y_{1,0}(\theta, \phi)=\sqrt{\frac{3}{4\pi}}\cos{\theta}\)、複合同順で\(\displaystyle Y_{1,\pm 1}=\mp \sqrt{\frac{3}{4\pi}}\sin{\theta}\exp{(\pm \rm{i}\phi)}\)です。
ここでの\(\rm{i}\)は虚数単位です。
これを利用すると、\(\displaystyle \cos{\theta}=\sqrt{\frac{4\pi}{3}}Y_{1,0}\)、\(\displaystyle \sin{\theta}\sin{\phi}=-\sqrt{\frac{2\pi}{3}}(Y_{1, 1}+Y_{1,-1})\)、\(\displaystyle \sin{\theta}\cos{\phi}=\sqrt{\frac{2\pi}{3}}\rm{i}\)\((Y_{1, 1}-Y_{1,-1})\)と書けることがわかります。
任意のベクトルは、これら3つの球面調和関数があれば表現することができます。
これを利用すると、遷移が許容されるための条件が導かれます。
こちらに示した積分\(I\)について、\(m\)に\(-1\)、\(0\)、\(+1\)を代入して、いずれも\(0\)となるとき、その遷移は禁制遷移となります。
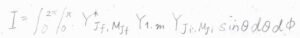
例えば、遷移双極子モーメントの\(z\)成分は、\(m=0\)のときの積分\(I\)の値に比例します。
\(x\)成分は、\(m=+1\)のときの\(I\)の値と\(m=-1\)のときの\(I\)の値の差に比例し、\(y\)成分は\(I\)の値の和に比例します。
ここからの考え方ですが、\(I=0\)になるかどうかの判定は、幾何の問題とすることで簡単になります。
角運動量保存則より、ベクトルである角運動量の足し算では、大きさと方向が保存されます。
状態\(\rm{i}\)の角運動量と遷移双極子がもつ角運動量の和は、かならず状態\(\rm{f}\)の角運動量となるはずです。
これを幾何の問題にすると、三辺の長さが\((J_\rm{i}\)\(、J_\rm{f}\)\(、1)\)の組み合わせの三角形が存在しないとき、このような遷移は禁制で、積分\(I=0\)ということになります。

したがって、遷移が許容されることの十分条件は、\(J_\rm{f}\)\(=J_\rm{i}\)\(+1\)となります。
状態\(\rm{i}\)と\(\rm{f}\)を逆にしても三角形を書くことができるので、\(J_\rm{f}\)\(=J_\rm{i}\)\(-1\)というのも十分条件になります。
また、\(Y_{J_\rm{f}, \mathit{M}_{\mathit{J}_\rm{f}}}\)\(^\ast Y_{1, m} Y_{J_\rm{i}, \mathit{M}_{\mathit{J}_ \rm{i}}}\)は常に実数である必要があるため、\(M_{J_\rm{f}}\)\(=M_{J_\rm{i}}\)\(+m\)と書けます。
図の中で\(m\)の値は、長さ\(1\)のベクトルの方向に対応します。
以上のことより、\(J\)の変化量\(\Delta J=\pm 1\)かつ\(\Delta M_J=0, \pm 1\)を満たす遷移だけが許容されるということになります。
フェルミの黄金律より、遷移確率が遷移モーメントの大きさの二乗に比例するため、極性の大きな分子ほどはるかに強度の大きいスペクトル線が観測されることになります。
回転量子数\(J\)が大きくなるほど、慣性モーメントは小さくなります。
\(J\)と\(J+1\)の間で励起と緩和が起こるとき、遷移双極子モーメントの大きさは、すべての\((M_J, m)\)の組み合わせで等しく、マイクロ波分光法の結果得られるピークの強度は、\(\displaystyle \frac{J+1}{2J+1}\mu_0^2\)に比例します。
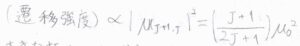
ここで、\(\mu_0\)は永久双極子モーメントの大きさで、外部から分子に一様な電場をかけることで縮退が部分的に解けるシュタルク効果を利用して、計算することができます。
回転量子数\(J\)が大きくなるほど、遷移双極子モーメントは小さくなり、電磁波と干渉しにくくなります。
そして、回転の量子数を2つもつ対称回転子においても、遷移双極子モーメントの大きさは上のようになります。
ここから、\(\Delta k=0\)という付加的な選択律があることがわかります。
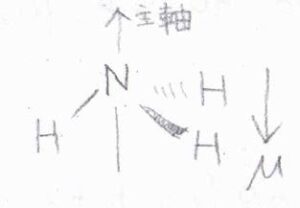
対称回転子では永久双極子モーメントと分子の主軸が平行であり、電磁波の照射で主軸の向きを変えることはできても、主軸から見て垂直な方向へ回転を加速させることはできません。
ピークの間隔
\(\Delta k=0\)より、対称回転子でも直線型回転子でも、吸収されるエネルギーは同じ式で書けます。
\(J\)から\(J+1\)への純回転遷移に対応する波数\(\tilde{\nu}\)は、\(2\tilde{B}(J+1)\)で与えられます。
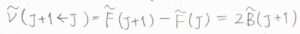
これは、分子が剛体であると仮定した結果ですが、実際には回転による遠心力で、化学結合が引き伸ばされたり結合角が変化したりという効果を考えたほうが測定結果によく合うことがあります。
遠心力による分子の変形を遠心ひずみと言い、経験的には剛体の波数から\(\tilde{D_J}J^2(J+1)^2\)という項を引くことで考慮されます。
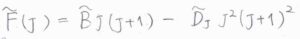
分子が引き伸ばされることで、慣性モーメントが大きくなるため、回転定数は見かけ上減少します。
\(\tilde{D_J}\)は遠心ひずみ定数と呼ばれ、二原子分子では\(\displaystyle \frac{4\tilde{B}^3}{\tilde{\nu_v}^2}\)という形で近似的に表すことができます。
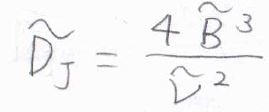
\(\tilde{\nu_v}\)は化学結合の振動波数で、結合の強さを表します。
強い結合であるほど、遠心ひずみが小さく、剛体としての式でも測定結果と合致しやすくなります。
遠心ひずみも考慮したときの吸収波数は、\(2\tilde{B}(J+1)-4\tilde{D}(J+1)^3\)と書けます。

一般的に、\(J\)が小さいときには第二項はとても小さいので、無視しても大きな問題はありません。
ピークの強度
最後に、スペクトルの強度について考えます。
先ほどもお話ししたとおり、個々の慣性モーメントの大きさは、回転量子数\(J\)が大きくなるほど小さくなります。
それとは別に、遷移前の状態の占有数が多く、遷移後の状態の占有数が少ないほど、遷移する分子数が多くなるため、スペクトルの強度が大きくなると考えられます。
そこで、ボルツマン分布を考えてみます。
回転の基底状態では、角運動量が\(0\)であり、\(\displaystyle \frac{N_J}{N_0}=g_J\exp{[-\frac{\hbar^2J(J+1)}{2I_\perp k_\rm{B}\mathit{T}}]}\)となります。
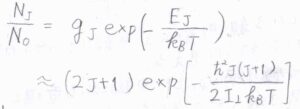
ここで、\(g\)は縮退度、\(k_\rm{B}\)はボルツマン定数、\(T\)は絶対温度です。
縮退度は、\(M_J\)のとりうる値の数であり、\(2J+1\)と書けます。
これにより、スペクトルの強度は\(J\)の増加に伴って単調減少せず、極大値をもつということが言えます。
マイクロ波吸収スペクトルの概形
実際に測定される回転スペクトルの概形は、こちらに示したようになります。

横軸が吸収波数、縦軸がマイクロ波の透過率です。
吸収された光が多いほど、グラフ上で大きな谷の形が現れます。
まず、回転遷移が起こったときの大きな特徴として、隣り合う吸収波数は互いに\(2\tilde{B}\)ずつ離れるため、等間隔となります。
厳密には遠心ひずみがあるので、高波数側で間隔が詰まってくることがあります。
ボルツマン分布の式を\(J\)で微分することで、占有数が極大をとるときの\(J\)を見積もることができて、それを\(J_\rm{max}\)とすると、直線型回転子で\(\displaystyle \sqrt{\frac{k_\rm{B}\mathit{T}}{2\mathit{hc\tilde{B}}}}-\frac{1}{2}\)と書けます。

厳密には、\(J\)がこれに最も近い\(0\)以上の整数のときに、占有数が最大となります。
ただし、スペクトルの強度は、占有数そのものではなく占有数の差で決まるため、\(J_\rm{max}\)と強度が最大となる回転量子数が必ずしも一致するとは限りません。
また、この回転スペクトルでは、主軸まわりの回転についての回転定数しかわからず、慣性モーメントの値も1つ、\(I_\perp\)しかわかりません。
硫化カルボニルなどのように長さが異なる化学結合をもっている場合は、それぞれの結合長を決定することはできません。
アンモニアでも、結合長と結合角をそれぞれ決定することはできません。
そこで、原子の1つを同位体に置換して回転定数を調べるということをします。
水素など小さな原子でなければ、同位体に置換したことによる換算質量の変化が小さく、結合距離は変化しないと近似でき、慣性モーメントの変化から個別の結合長や結合角を決定することができます。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




