こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(isothermal and adiabatic process)
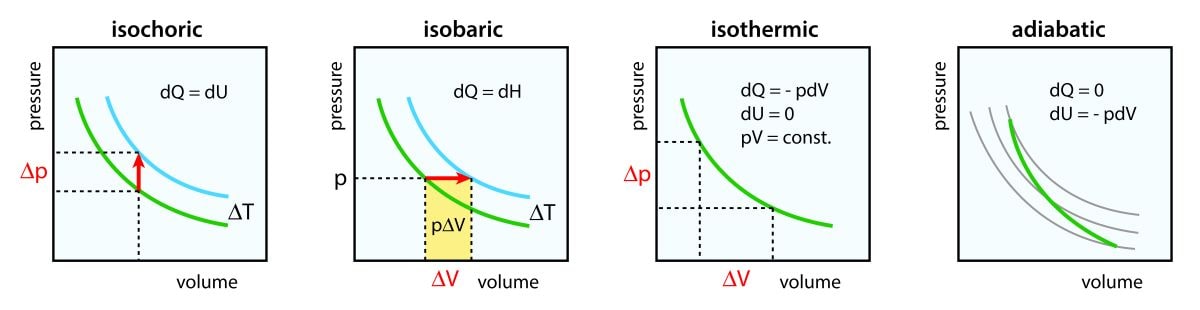
定積変化、定圧変化については、別の記事ですでに話しているので、こちらを参照してください。
それでは内容に入っていきます!
前提
まず今回考える系は、理想気体であるとします。
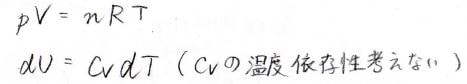
そして、熱容量の温度依存性も、今回はないものとして話を進めていきます。
熱容量の温度依存性については、こちらを参照してください。

等温変化
はい、それでは等温変化に入っていきます。
温度一定条件で変化させるため、内部エネルギーの変化量\(\Delta U\)も\(0\)ということになります。
したがって、熱力学第一法則より、系に与えられた熱量\(q\)と系にされた仕事\(w\)を足すと\(0\)になります。
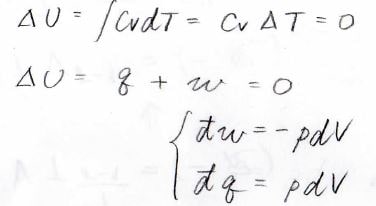
微小量で考えると、\(\rm{d’}\)\(w=-p\rm{d}\)\(V\)となるため、\(\rm{d’}\)\(q=p\rm{d}\)\(V\)となります。
\(p\)-\(V\)グラフ上で等温変化を考えると、こんな感じになります。
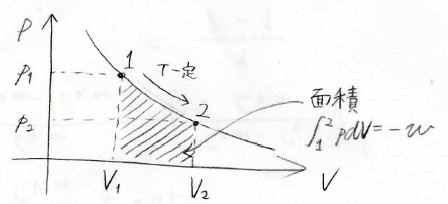
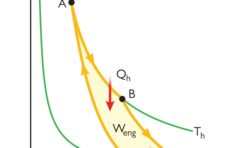
ここでは状態\(1\)から状態\(2\)への等温膨張の例を示しており、系が外部にした仕事\(-w\)は\(pdV\)の定積分、すなわちグラフ上で斜線で示した面積に等しくなります。
圧力\(p\)と体積\(V\)に、それぞれの状態の番号を添え字として付けることにすると、\(w\)は、このような式で表されます。
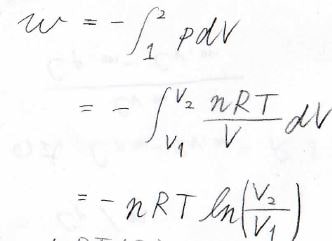
ここで、理想気体の状態方程式より\(p=nRT/V\)であるため、結局\(w\)は\(-nRT\ln{({V_2}/{V_1})}\)となります。
また、体積の比をひっくり返すと圧力の比になるため、\(w\)は\(nRT\ln{({p_2}/{p_1})}\)と表すこともできます。
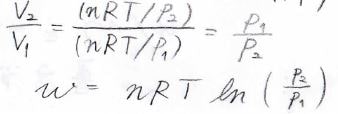
断熱変化
はい、等温変化についてはここまでで、次に断熱変化を見ていきます。
断熱変化とは、熱の出入りがなく、内部エネルギーの変化量が系に与えられた仕事と等しくなる変化の仕方です。
系が理想気体であることを考えると、これら2つの内部エネルギーの式を合わせることで、体積と温度の関係式が得られます。
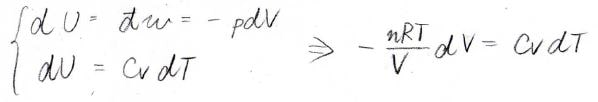
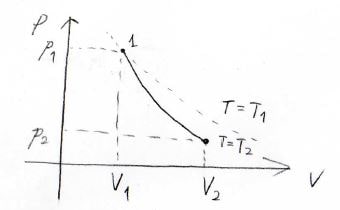
\(p\)-\(V\)グラフで断熱膨張を表すと、こんな感じになってまして、必ず温度は減少します。
それで、先ほどの関係式の両辺を状態\(1\)から状態\(2\)まで定積分することを考えると、今\(C_\rm{V}\)は温度依存性を無視できるとしているため、積分の外に出せて、こんな形になります。
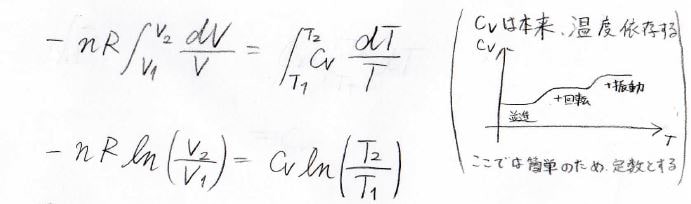
両辺の\(\exp\)をとると、こんな形になりまして、さらに、両辺に\(V_2^{nR}T_1^{C_V}\)をかけて、それを\(1/{nR}\)乗すると、\(VT^{C_V/{nR}}\)の値が状態\(1\)と状態\(2\)で変わらないことになります。
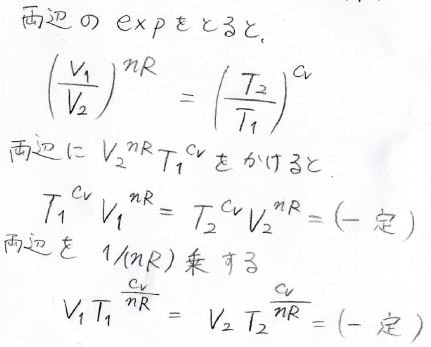
これが、断熱過程における状態量の変化を表す式であり、ここからさらに変形することが可能です。
例えば、\(nR\)はMayerの式より、理想気体の定圧熱容量と定積熱容量の差に等しいので、それぞれのモル熱容量を\(C_{V, \rm{m}}\)、\(C_{p, \rm{m}}\)として表すことにすると、\(T\)の指数は\(C_{V, \rm{m}}/(C_{p, \rm{m}}-C_{V, \rm{m}})\)となります。

さらに、\(C_{V, \rm{m}}\)と\(C_{p, \rm{m}}\)の比を\(\gamma\)とすると、先ほどの値は\(1/(\gamma-1)\)となります。

したがって、\(VT^{1/{\gamma-1}}\)は一定であり、これを\(\gamma-1\)乗することで、\(TV^{\gamma-1}\)も一定であることになります。
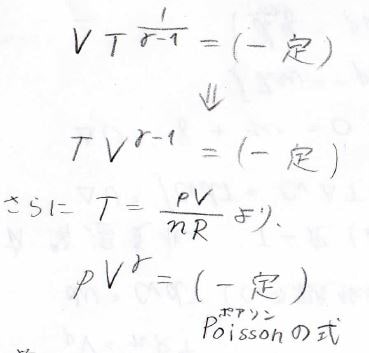
また、理想気体の状態方程式より\(T=pV/{nR}\)なので、\(pV^\gamma\)も一定になります。
この式は、Poissonの式と呼ばれ、この式だけを知っている方も多いと思います。
最後に、\(\gamma\)がどういった値となるのかを確認しておきますと、これは熱容量の比であり、単原子分子や低温の気体分子では\(5/3\)、すなわち\(1.66\)…となります。
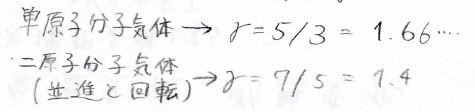
二原子分子で並進と回転が自由度として寄与する場合には\(7/5\)で\(1.4\)となります。
Mayerの式および熱容量の温度依存性と自由度の関係については、こちらの記事を参照してください。

まとめ
はい、それでは今回の内容は以上なので最後軽くおさらいをやって終わります。
今回は等温変化と断熱変化について考えていきました。
理想気体であることを前提にした場合、温度一定下では、内部エネルギーの変化量が\(0\)なので、系に与えられた熱量と系が外界へした仕事が等しくなります。
その仕事の大きさは、\(p\)-\(V\)グラフ上で面積として表すことができ、仕事は自然対数で与えられます。
断熱変化に関しては、内部エネルギーの変化量が\(-p\rm{d}\)\(V\)で、\(C_V\)\(\rm{d}\)\(T\)でもあるので、そこから温度と体積の関係式が出てきます。
また、その関係を使うと、定積熱容量と定圧熱容量の比を\(\gamma\)として\(pV^\gamma\)が一定になるというPoissonの式も導くことができます。
以上です。ありがとうございました!