こんにちは！
それでは今日も化学のお話やっていきます。
今回のテーマはこちら！
動画はこちら↓
動画で使ったシートはこちら(adsorption)
それでは内容に入っていきます！
固体表面で起こる変化
固体表面では、多種多様な物理、化学現象が起こります。
たとえば、溶解は、固体表面にある分子から先に溶媒へと逃げていく表面現象です。
また、不均一触媒は、反応物の活性な構造を固体表面で安定化させることで、反応を加速させます。
電池や電解槽も、電極表面における酸化還元反応を半反応としています。
表面析出、蒸着、エッチングは、いずれも表面加工に用いられる方法です。
まず蒸着は、真空中で物質を蒸発させて、固体表面に膜を作る方法で、レンズやミラー、ディスプレイなど光学部品に広く活用されています。
表面析出は、原子が表面に積み重なって層を形成する現象のことで、エッチングは、腐食作用によって固体表面を削りとる技法のことをいいます。
これらは集積回路を作るために必要であるため、半導体産業で特に重要な現象です。
一般的に、これら固体表面で起こる変化は、気相や液相バルク中の反応に比べて、素反応が多いという特徴があります。
したがって、反応速度も多くの要因によって左右されることになります。
表面の成長
ここからは、吸着を考えることで、表面におけるさまざまな素反応について考えていきます。
吸着とは、粒子が表面に付着することを意味する言葉で、反対に表面に付着していた粒子が放出されることを脱着といいます。
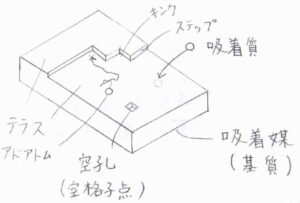
付着する物質のことを吸着質、吸着の下地となる物質のことを吸着媒、もしくは基質と呼びます。
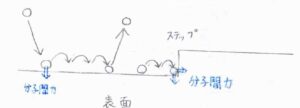
吸着媒表面に近づいてきた吸着質は、はじめ大きな運動エネルギーをもっているため、すぐに静止するわけではなく、表面付近で複数回バウンドします。
表面との相互作用により、分子は飛び跳ねる度にそのエネルギーを失いますが、その程度は小さいため、多くは運動エネルギーを失って捕捉されるよりも前に相互作用のポテンシャルから抜け出すことになります。
ただし、吸着媒の表面構造に欠陥がある場合は、話が変わります。
表面が平坦である場合と比較して、欠陥のある表面ではより多くの原子と相互作用するため、分子を捕捉しやすくなります。
たいていの場合、新しくできた表面も気体に曝されているため、速やかに次の分子に覆われることになります。
このようにして、固体表面の進行は進んでいきます。
不均一触媒反応も、表面欠陥の存在が重要な役割を果たします。
表面欠陥の名称
平坦な原子層はテラスと呼ばれており、2つのテラスの間にできる段差のことはステップといいます。
そのほかに、ステップが交差したキンクや、表面に吸着した原子であるアドアトム、格子の欠陥である空孔(空格子点)などが代表的な表面欠陥の例です。
固体表面の様子は、実験を通じて可視化することが可能で、表面の組成や欠陥を観察することに利用されています。
電子顕微鏡や走査プローブ顕微鏡、原子間力顕微鏡などの方法がありますが、測定原理については、学会やメーカーのサイトのほうがよほど詳しく書いてありますので、ここでは説明を省きます。
参照のリンクを貼っていますので、また時間あれば読んでみてください。
走査型電子顕微鏡(SEM): https://www.jaima.or.jp/jp/analytical/basic/em/sem/
透過型電子顕微鏡(TEM): https://www.jaima.or.jp/jp/analytical/basic/em/tem/
走査プローブ顕微鏡(SPM): https://www.jaima.or.jp/jp/analytical/basic/em/spm/
原子間力顕微鏡(AFM): https://www.spsj.or.jp/equipment/news/news_detail_22.html
(1~3つ目は日本分析工業会、4つ目は高分子学会)
吸着過程の熱力学的な解釈
吸着を熱力学的に考えると次のようになります。
熱力学第二法則より、定温定圧条件下でギブズエネルギー変化が負となるのが自発的な変化ということですが、吸着により並進の自由度が減る分だけエントロピーは減少すると考えられます。
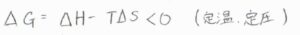
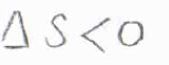
つまり、エントロピーだけで考えれば、吸着は不利な反応だといえます。
したがって、吸着が起こるためには、吸着により大きな安定化が起こらなければならないため、多くの場合、吸着は発熱過程となります。
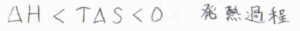
ただし、例外もあります。
ガラス表面に吸着した水素分子は、解離して原子となり、ガラス表面を自由に動き回ることになります。
その結果、並進エントロピーが大幅に増大するため、ガラスへの水素分子の吸着が吸熱過程であるにも関わらず、吸着が起こるということになります。
表面の成長速度
また、吸着を繰り返して表面が成長する速さは、吸着媒と吸着質の衝突頻度に比例すると考えられます。
吸着媒1分子あたりの衝突頻度\(Z\)は、\(AZ_\rm{w}\)\(/N\)で与えられます。
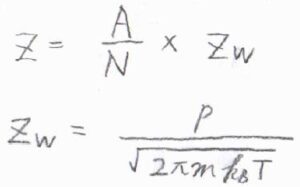
ここで、\(A\)は吸着媒の表面積、\(N\)は吸着媒表面にある分子数、\(Z_\rm{w}\)\(\)は衝突流束です。
衝突流束は、以前の記事でお話ししましたが、単位面積あたりの衝突頻度のことです。
詳しくは、こちらをご参照ください。
吸着質が理想気体であるとすると、衝突流束は\(p/\sqrt{2\pi mk_\rm{B}\mathit{T}}\)で与えられます。
ここで、\(p\)は気体の圧力、\(m\)は気体分子の質量、\(k_\rm{B}\)\(\)はボルツマン定数、\(T\)は絶対温度です。
実際に求めるときには、こちらのように定数部分をまとめると便利です。
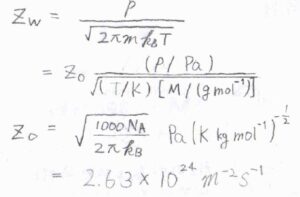
物理吸着と化学吸着
続いて、吸着は2種類に大別できるという話をします。
まず、物理吸着は、吸着質と吸着媒のファンデルワールス相互作用による吸着です。
その起源は双極子間の静電的な相互作用であるため、距離が離れていても引力がはたらきますが、吸着によって放出されるエネルギーは、凝縮エンタルピーと同程度(\(\lt -20\ \rm{kJ\ mol^{-1}}\)\(\))であり、そこまで強い吸着とはいえません。
吸着質が吸着媒の表面を跳ね回っている間、ファンデルワールス相互作用によって次第にエネルギーを失い、最終的に吸着するまでの過程のことは、適応と呼ばれます。
物理吸着に対して、吸着質と吸着媒の間に化学結合(多くは共有結合)が形成される吸着のことを化学吸着といいます。
その起源は、量子力学によって説明され、力の大きさは遠距離になるほど著しく減少していきます。
しかし、吸着エンタルピーは物理吸着の十数倍程度(\(-500\sim -200\ \rm{kJ\ mol^{-1}}\)\(\))であり、比較的強い吸着様式であるといえます。
先ほどもお話ししたとおり、吸着媒表面の欠損がある場所では、より多くの原子と相互作用できるため、吸着質は配位数が最大となる場所に吸着しやすいことになります。
また、これは物理吸着した後の状態についてですが、吸着した分子の近くには、まだ原子価が満たされていない活性な原子が存在しているため、分子が分解してフラグメントになることで、さらにエネルギー的に有利な構造となれる場合があります。
このような化学吸着のことを解離性化学吸着といいます。
活性化過程と非活性化過程
解離型化学吸着に至る過程には次の2種類があります。
まず、こちらのグラフは、縦軸にポテンシャルエネルギー、横軸に表面からの距離をとったものです。
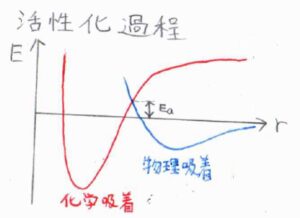
赤い線がフラグメントの化学吸着、青い線が分子の物理吸着のポテンシャルを示しています。
はじめ、吸着質と吸着媒の距離が遠いときには、長距離力であるファンデルワールス力が優勢にはたらくことで、物理吸着が起こります。
その後、フラグメントとして化学吸着したほうがさらにエネルギー的に有利であれば、赤のポテンシャルに移ります。
その過程で、ポテンシャルは一度上がるため、吸着および脱着の素反応は、活性化エネルギーを有し、アレニウス的な振る舞いをするということになります。
これは非解離型の吸着についても同じです。
さらに、その活性化障壁が遠くで静止している分子のエネルギーを超えるときには、物理吸着で放出されるエネルギー以上に多くのエネルギーが必要になるため、そうでない場合よりも進行が遅くなります。
こういった化学吸着の過程を活性化過程といい、そうでないものを非活性化過程といいます。
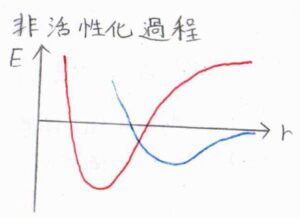
清浄な金属表面に対する気体の吸着は、そのほとんどが非活性化過程となります。
被覆率(表面被覆率)
そして多くの場合、吸着エンタルピーは、現時点においてどれだけ吸着が起こっているかによって、変化するということが知られています。
その大きな理由は、吸着質どうしが相互作用するためです。
そこで、表面の被覆の程度を表す量として、被覆率(表面被覆率)というものを考えます。
ここでは、\(\theta\)と表すことにします。
被覆率は、吸着点の総数に対するすでに占有されている吸着点の数の比率として定義され、\(V/V_\infty\)とも書かれます。
ここで、\(V\)は吸着している吸着質の量に相当する自由気体の体積です。
\(V_\infty\)は完全な単分子層被覆を形成するのに必要な吸着質の量に相当する体積です。
\(\theta\)が大きいとき、空の吸着点に吸着質が接近する頻度は低いため、吸着速度は遅くなると考えられます。
長時間が経過すると、吸着速度と脱着速度がつりあうことで、動的な平衡状態に至ります。
そのときの被覆率は、圧力や温度によって変化します。
ある温度について、平衡状態に至った\(\theta\)と圧力の関係を表した式は、吸着等温式と呼ばれており、これまでさまざまな形の等温式が提案されてきました。
吸着等温式の具体例については、次回の記事で解説していきます。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました！
