こんにちは！
それでは今日も化学のお話やっていきます。
今回のテーマはこちら！
動画はこちら↓
動画で使ったシートはこちら(phase diagram of ternary system)
それでは内容に入っていきます！
ギブズの相律
始めに、ギブズの相律を思い出してみましょう。
ギブズの相律とは、成分の数と共存する相の数から、独立な変数の数、つまり自由度がわかるという規則です。
式は、\(F=C-P+2\)であり、\(F\)が自由度、\(C\)が成分の数、\(P\)が共存する相の数です。
詳しくは、こちらの記事を参照してください。
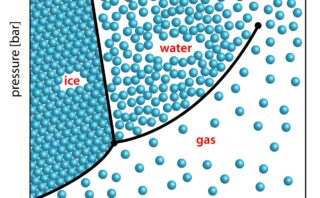
3成分系のときには、\(C=3\)ですから、\(F=5-P\)となります。
さらに、温度と圧力を固定した場合の図を書くときには、ここから\(2\)を引いて、\(F=3-P\)となります。
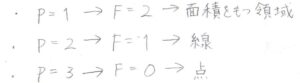
このとき、1相状態では、\(F=2\)となるため、これは、相図の中で面積を持つ領域として現れることになります。
2相共存状態では\(F=1\)ですから、2つのモル分率に関係があるということで、相図の中で線となって現れます。
3相共存状態は\(F=0\)ですから、モル分率はいずれも独立に変化できません。
したがって、相図の中で点として現れます。
三角形相図
それではここから、実際に3成分系の相図を書いていきます。
ここでは、温度と圧力を一定としています。
相分離が起こらない系
まずは、相分離が起こらないパターンについて考えます。
3つの成分\(\rm{A}\)\(\)、\(\rm{B}\)\(\)、\(\rm{C}\)\(\)のモル分率を\(x_\rm{A}\)\(\)、\(x_\rm{B}\)\(\)、\(x_\rm{C}\)\(\)として、\(x_\rm{A}\)\(+x_\rm{B}\)\(+x_\rm{C}\)\(=1\)が成り立ちます。
その相図は、こちらのような三角形で表すことができます。
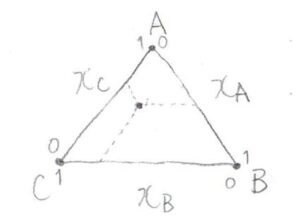
三角形の頂点は、いずれかの成分の1成分系に対応し、三角形の辺は、いずれかの成分の2成分系に対応します。
ある点について、そこからどれか1辺に平行な線を伸ばしていき、その半直線と辺の交点をその点におけるモル分率とします。
相分離が起こる系
これを基本として、ここからは相分離があるパターンを見ていきます。
\(\rm{B}\)\(\)と\(\rm{C}\)\(\)が部分可溶なとき
それではまず、成分\(\rm{B}\)\(\)と\(\rm{C}\)\(\)が部分可溶な温度のときの相図を考えてみましょう。
圧力を固定して三角柱の相図を書くと、下図左側のようになります。
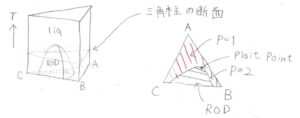
高さが温度です。
これをある高さで切り取った断面が、その温度における三角形の相図となります。
右にあるのがその断面です。
赤く塗られているところが液相1相状態、塗られていないところが相分離領域、略してRODです。
ここの組成は巨視的には存在せず、液相が2相に分離します。
RODの中の線は、連結線(tie line)を示しています。
一般的に、三角形の相図にある連結線は、互いに平行とはなりません。
そして、ちょうど相分離が起こらなくなる点のことをプレートポイントと呼びます。
2成分系については、こちらを参照してください。
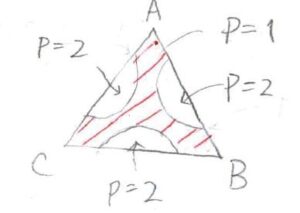
\(\rm{B}\)\(\)と\(\rm{C}\)\(\)、\(\rm{A}\)\(\)と\(\rm{B}\)\(\)、\(\rm{C}\)\(\)と\(\rm{A}\)\(\)が部分可溶なとき
それで、先ほどは成分\(\rm{B}\)\(\)と\(\rm{C}\)\(\)の間でだけ相分離が起こることを考えましたが、さらに\(\rm{A}\)\(\)と\(\rm{B}\)\(\)、\(\rm{C}\)\(\)と\(\rm{A}\)\(\)の組み合わせでも部分可溶となる場合は、このような相図になります。
さらに、ここから温度を低下させると、RODは拡大していき、下の図のように合体することがあります。
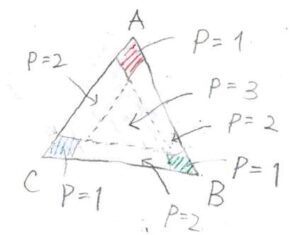
このとき、頂点付近が液相1相で、合体前のように連結線が引ける領域が液相2相状態、それ以外の中心周辺が液相3相状態となります。
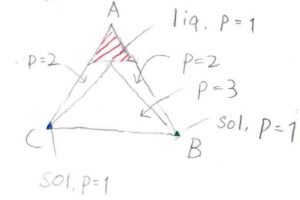
水と2種類の塩の場合
また、水を成分\(\rm{A}\)\(\)として、それによく溶ける固体の塩\(\rm{B}\)\(\)と\(\rm{C}\)\(\)という3成分系では、こんな形の相図になります。
2成分の温度-組成図を先に見たほうがわかりやすいと思います。
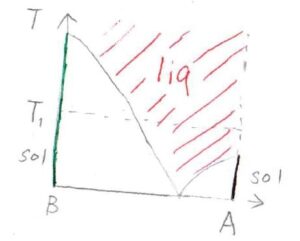
塩が少ないときには溶液となり、塩が多いときには、一部が溶け残りとなります。
これを三角形相図にすると、成分\(\rm{A}\)\(\)に対応する頂点の周辺、つまり水を多く含む組成では、液相1相となる領域が存在し、頂点\(\rm{B}\)\(\)、\(\rm{C}\)\(\)付近では溶け残りの固相との共存状態となります。
共融混合物を作る場合
\(\rm{A}\)\(\)と\(\rm{B}\)\(\)、\(\rm{B}\)\(\)と\(\rm{C}\)\(\)、\(\rm{C}\)\(\)と\(\rm{A}\)\(\)の間でそれぞれ共融混合物を作る場合には、三角柱の相図は下図の左側のようになります。
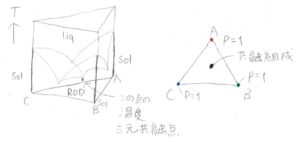
わかりにくいとは思いますが、注目していただきたいのは、それぞれ2成分の共融混合物同士がさらに共融混合物をつくることで、融点が下がることがあるということです。
いちばん融点が低くなった点を、三元共融点と呼びます。
そして、三元共融点と同じ温度で断面をとると右のような三角形相図になります。
頂点付近は、各成分を主とする固相1相状態に対応します。
それから、共融組成の点が中心付近に現れます。
2成分系については、こちらを参照してください。
ステンレス鋼
最後に、鉄、クロム、ニッケルの合金であるステンレス鋼の相図を見て終わりたいと思います。
その相図はこんな感じで、これまで見てきた形よりもはるかに複雑になります。
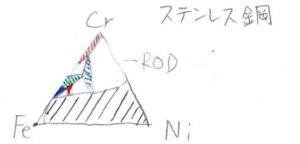
ここでは、共融混合物だけではなく、化合物の形成も考えなくてはいけません。
合金以外でも、溶媒と界面活性剤と塩を混合したミセルを作るような系では、温度や濃度によってミセルの形状を変化させたり、白濁、沈殿したりするので、複雑な相図になることが多いです。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました！
