こんにちはー!今回も化学のお話やっていきます。今回のテーマはこちら!
動画で使ったシートはこちら(perturbation)
では早速行きましょう!
摂動法の計算条件
前回の記事でもお話ししましたが、まずは摂動法がどういうものかもう一度説明します。
摂動法ではまず、ハミルトニアンをこんな風に置き換えます。

\(\hat{H}’\)というのが補正項、\(\hat{H}_0\)は補正がない時、すなわちそのままでも解ける単体問題のハミルトニアンです。
\(g\)というのはただの定数です。
そして、ハミルトニアンに補正を加えるとなると当然エネルギーが変わってきますし、波動関数も変わります。
そこで、この2つはこのように\(g\)のべき級数の形で考えます。
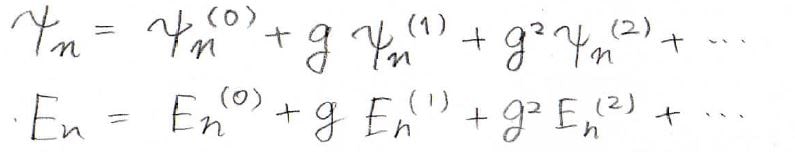
この形であればシュレディンガー方程式が解ける状態のまま、補正の効果を考えることができます。
ここで\(n\)は量子数、()の中の数字が補正項の次数です。
(0)というのは補正してないという事なので、\(\psi _n^{(0)}\)と\(E_n^{(0)}\)は補正する前の値という事になります。
シュレディンガー方程式の係数比較
ではこれらをシュレディンガー方程式に入れてみましょう。

すると両辺が定数\(g\)のべき級数になるわけですが、この等式が常に成り立つという場合、各項の係数が同じにならないといけません。
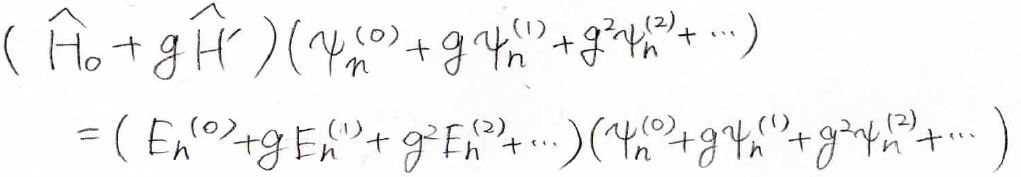
例えば\(g^0\)の係数を取り出してみると、\(\hat{H}_0\psi_n^{(0)}=E_n^{(0)}\psi_n^{(0)}\)となりますが、これは補正をする前のシュレディンガー方程式です。

同じように\(g^1\)についてはこんな感じです。

\(g^2\)についても、等式が成り立っているという事になります。

波動関数とエネルギーの補正項
直交系の線形結合を利用
さてここから波動関数とエネルギーの補正項を考えていきたいんですけど、その時に補正前の波動関数が直交性を満たすことを利用します。
高校の数学でやったベクトルと同じように考えてもらえばいいんですけど、一次独立な2つの二次元ベクトルがあったときには、平面上の任意のベクトルは、この2つのベクトルの線形結合で表すことができます。

これと同じように互いに平行とならない\(\psi_n^{(0)}\)達の線形結合で任意の波動関数を表すことができます。
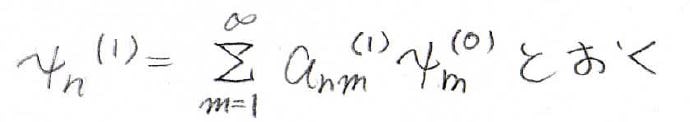
ここでは仮に係数部分を\(a_{nm}^{(1)}\)としてこんな風に表すことにします。
エネルギーの一次補正項
それで先ほどの\(g^1\)に関しての等式に代入してみるとこうなります。
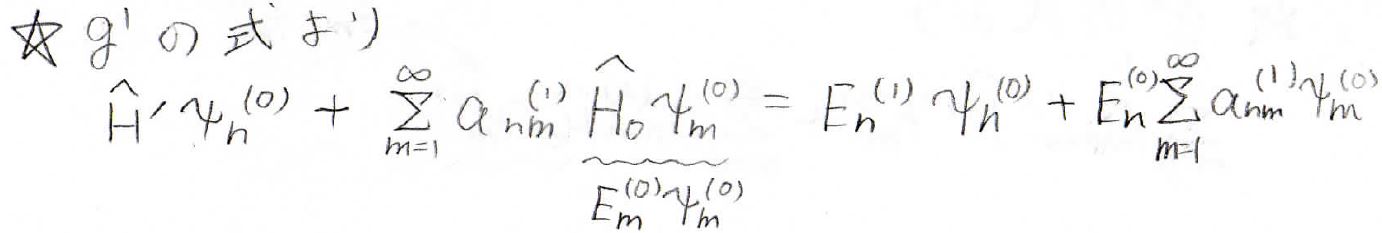
ここで\(\hat{H}_0\psi_n^{(0)}\)の部分は補正前のエネルギー\(E_n^{(0)}\)が固有値になります。
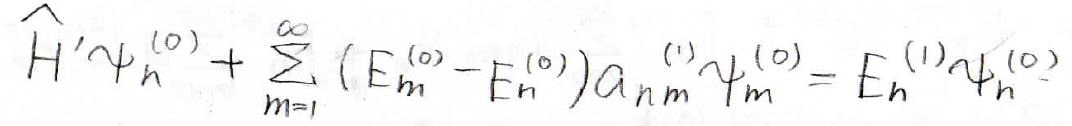
そしてまず、エネルギーの補正項を考えるためにどうするかというとこの式の両辺に左から\(\psi _n^{(0)}^\ast\)をかけて全空間で積分します。
始めに、左辺だけやってみましょう。

ここで第二項目に注目すると、\(E_n^{(1)}\)と\(a_{nm}^{(1)}\)は定数なので積分の外に出せて結局\(\psi_n^{(0)}^\ast\)\( \psi_n^{(0)}\)の積分になっています。
ここで、\(\psi_n^{(0)}\)は直交性を満たしているので\(n\)と\(m\)が異なる場合、この積分は\(0\)になります。
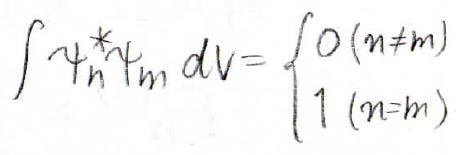
それで\(n\)と\(m\)が等しい場合はどうかというと、このエネルギーの差が\(0\)になります。
つまりこの項は\(0\)になるという事が分かります。
そのため残るのはこの第一項だけです。
では今度右辺を見てみると、こうなってて、エネルギーは積分の外に出せるので、結局規格化条件より、\(E_n^{(1)}\)のみとなります。
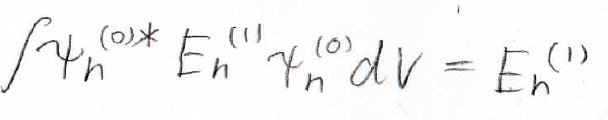
そして左辺=右辺より最終的に、この式が得られます。
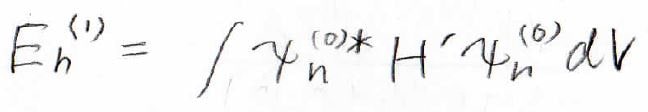
これはエネルギーの一次の補正項が補正前の波動関数とハミルトニアンの補正項から計算できるという事を表しています。
波動関数の一次補正項
では今度、波動関数の補正も考えていきましょう。
そのためにはさっき\(\psi _n^{(0)}^\ast\)をかけたところを\(\psi_m^{(0)}^\ast\)に変えて、また左からかけて積分します。
すると、まず左辺はこのようになります。
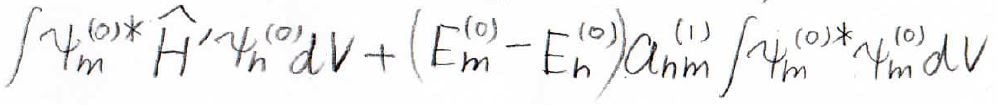
また、右辺では直交性より\(0\)となることがわかります。

左辺\(=0\)という式より、\(a_{nm}^{(1)}\)がこんな風に出てきます。
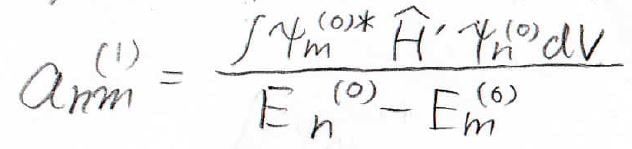
\(a_{nm}^{(1)}\)がすべてわかれば\(\psi_n^{(1)}\)、すなわち波動関数の一次の補正項が分かったことになります。
エネルギーの二次補正項
補正項は無限にあるので全てをやりつくすことはできませんが、もっと高次の項も同じようにできますので、最後にエネルギーの二次の補正項を最後に出して終わります。
\(\psi_n^{(2)}\)も先ほど同様補正前の波動関数の線形結合で書けるものだと考えます。
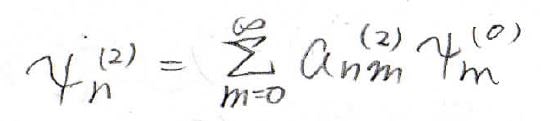
それでシュレディンガー方程式の\(g^2\)に関する等式に代入してみるとこんな感じの式になります。
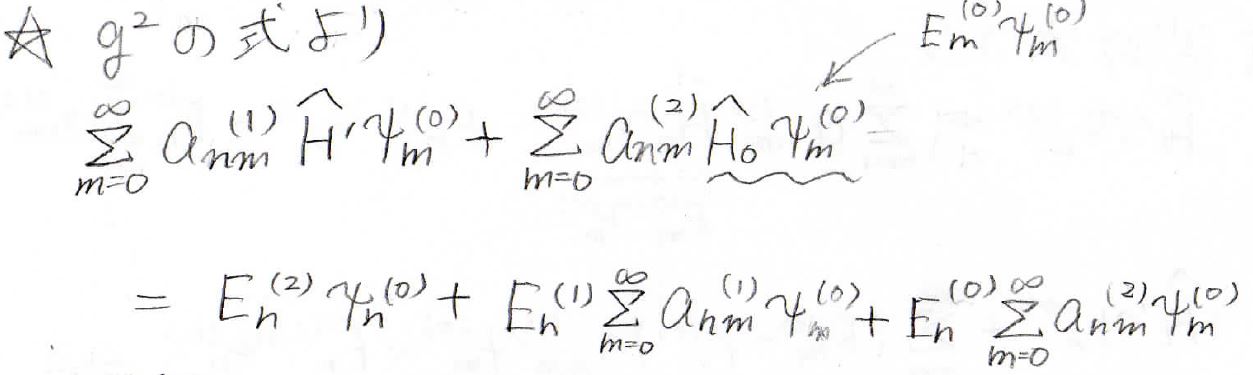
ここに左から\(\psi_n^{(0)}^\ast\)をかけて積分すると、先ほどのようなキャンセルが左辺の第二項と右辺の第三項で起こります。
それで右辺の第二項を移項すると、左辺の\(\Sigma\)のなかで\(n=m\)の場合だけがキャンセルすることになって、結局、↓の形でエネルギーの二次の補正項が出てくるということになりました。
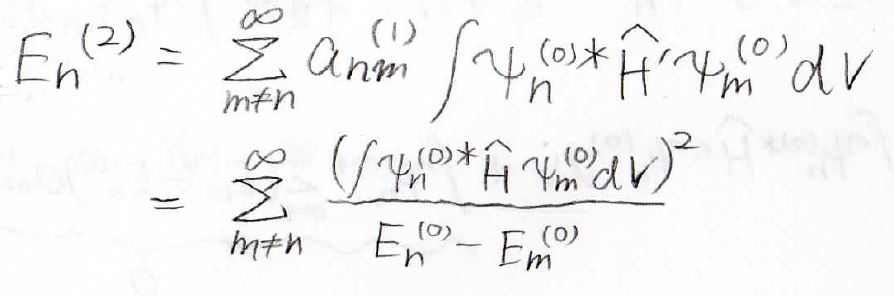
まとめ
今回は練習問題ありませんので、最後おさらいをやって終わります。
今回は摂動法についてハミルトニアンの補正によって波動関数とエネルギーがどのように変わるのかというお話をしました。
べき級数にすることで計算は簡単だけど、愚直にやっていけば解けるよねという形になっています。
さらに、補正前の波動関数を使ってベクトル同様に任意の波動関数を表現するというのも知ってほしいテクニックになります。
ということで今回は以上です。
それではどうもありがとうございました!



