こんにちは!
今回のテーマはこちら!
動画はこちら↓
動画で用いたシートはこちら(bremsstrahlung)
制動放射とは
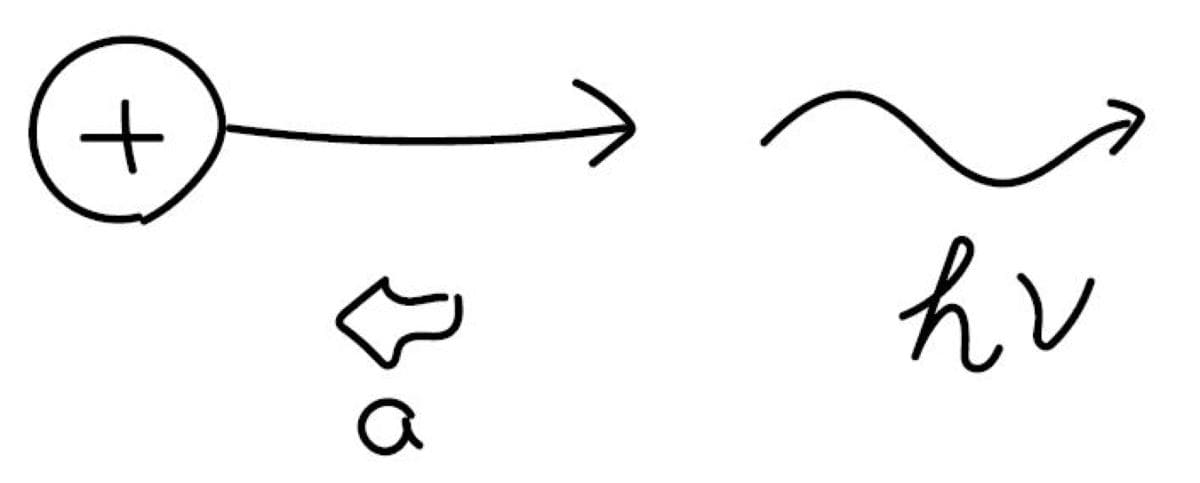
制動放射とは、電荷を帯びた物体が加速度を受けたときに、電場と磁場の揺らぎ、すなわち電磁波が生じる現象です。
この現象は、原子がどういうものかを考えるうえで重要なものです。
まずはその話の前に、実際にどんな場面で制動放射という現象がみられるのかという話からします。
制動放射の例 蛍光灯
まず1つ目の例は蛍光灯です。
LEDではない昔ながらの蛍光灯が光る原理こそが、この制動放射です。
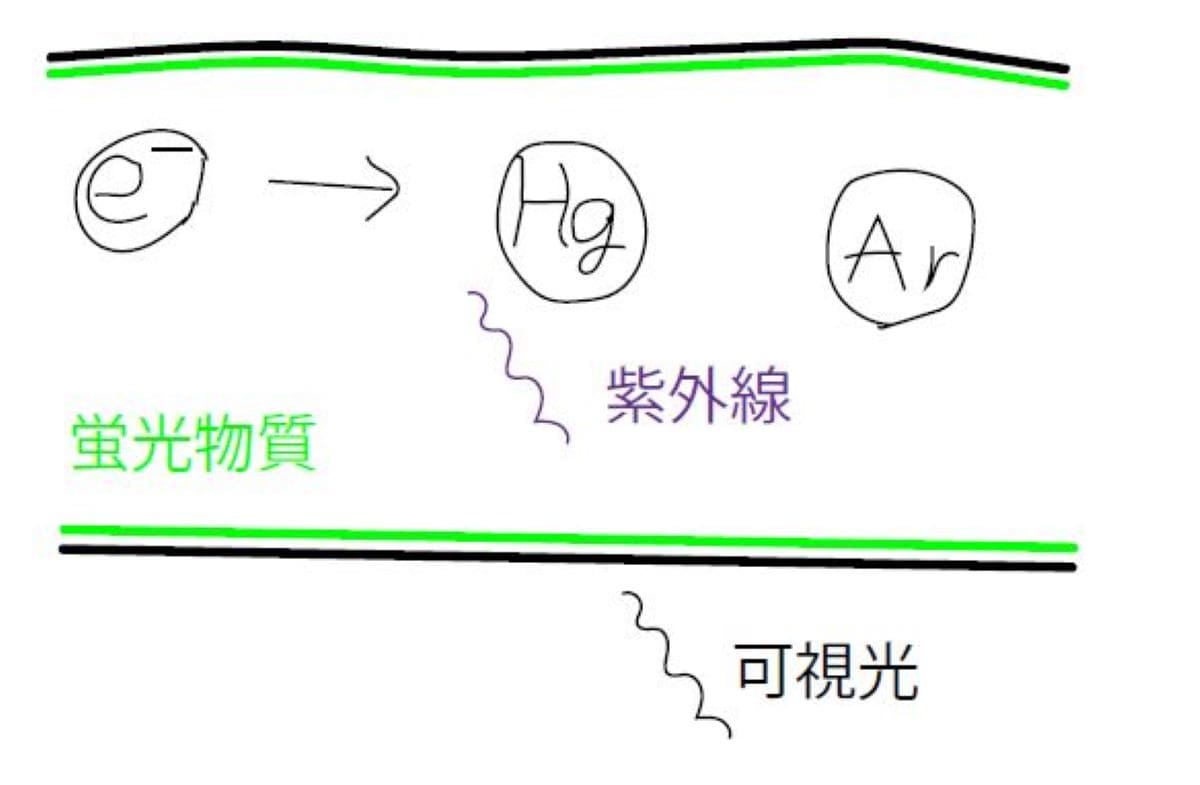
上記は蛍光灯の断面のイメージです。
まず、ガラスの管の中はアルゴンで満たされています。
管の中には水銀の合金が入れられており、電源をつけたときに陰極のフィラメントが温まりだし、管の中に水銀の蒸気が満たされる状態になります。
それと同時に印加電圧によって、フィラメントからエネルギーの高い電子が飛び出して陽極に向かおうとします。
電子が水銀原子と衝突したときに、電子は水銀原子から力を受けて、電磁波が発生します。
しかし、蛍光灯の場合、この電磁波は紫外線で、このままでは有害なだけであまり明るくありません。
そこで蛍光管の内壁に蛍光物質を塗布しておき、紫外線を可視光に変換して、明るい蛍光灯となっています。
制動放射の例 X線光源
2つ目の例はX線光源です。
X線とは、波長が\(1\ \rm{pm}\)\(\sim 10\ \rm{nm}\)と非常に短く、大きなエネルギーを持っている電磁波です。
透過性が高く、レントゲンなど医療への利用の他、結晶やミセルなどの微細な構造の研究にも使われています。
シンクロトロンなど少し違うものもあるのですが、今回はX線光源の基本的な原理をお話しします。
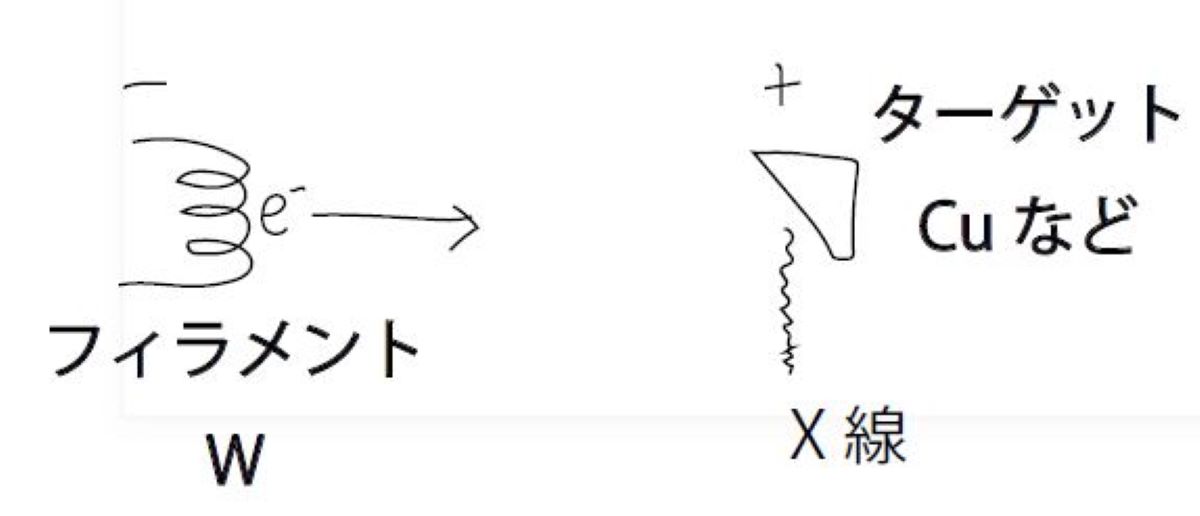
蛍光灯と同様にまず電圧をかけることで、融点の高いタングステンなどでできたフィラメントから熱電子を飛び出させます。
さらに、電子に高電圧を印加し、加速させた状態で、陽極側のターゲット物質に衝突させることで、X線が生じます。
ここの衝突でも、大きな熱が発生するのでターゲットも融点が高い必要があり、モリブデンやタングステンが使われます。
そこまで高エネルギーでない場合は銅がターゲットに使われることもあります。
ただし、ここで注意したいのが、出てくるX線のすべてが制動放射によって出てくるわけではないという事です。
下のグラフは各波長ごとに出てくるX線の強度を表したものです。

クジラに例えられることもあるのですが、鋭いピークが何本かと弱くてブロードなピークが1つという形になることが知られています。
制動放射が由来のX線は、強度が弱く、広い周波数範囲をもつほうで、こちらのX線は連続X線と呼びます。
連続X線は、電子の持っていたエネルギーが失われることで発生するので、もともとどれだけ高いエネルギーを持っていたかによって、最小の波長は決まります。
もう一方の鋭いピークは、特性X線といって、ターゲット物質によって波長が決まります。
特性X線が発生する原理は、飛び出していった電子がターゲット原子の内殻側の電子を弾き飛ばすことから始まります。
電子角のエネルギーは内殻、動いた電子がもともと入っていた電子殻と新たに入った電子殻のエネルギー差に相当する電磁波が発生します。
これが、特性X線です。
状態間のエネルギー差は物質に固有なので、特性X線の波長はターゲットの元素によって変わります。
制動放射は原子の存在を否定する?
ここまで制動放射の例を見ていきましたが、ここからはなぜ制動放射が原子の構造を考えるうえで重要になってくるのかというお話をします。
結論から言うと、制動放射は高校の物理でも習うボーアの原子モデルを否定する現象だからです。
どういうことか説明する前に、まずはボーアの原子モデルについて復習します。
原子が正電荷をもつ部分と負電荷をもつ部分が組み合わさってできていることはわかっていましたが、実際にどのように原子ができているのかは長らく謎のままでした。
そこで、当時の科学者たちは原子モデルを提案していきました。
その1つがこのボーアの原子モデルです。
ボーアのモデルでは、電子は原子核を中心に等速円運動をしていると考えています。
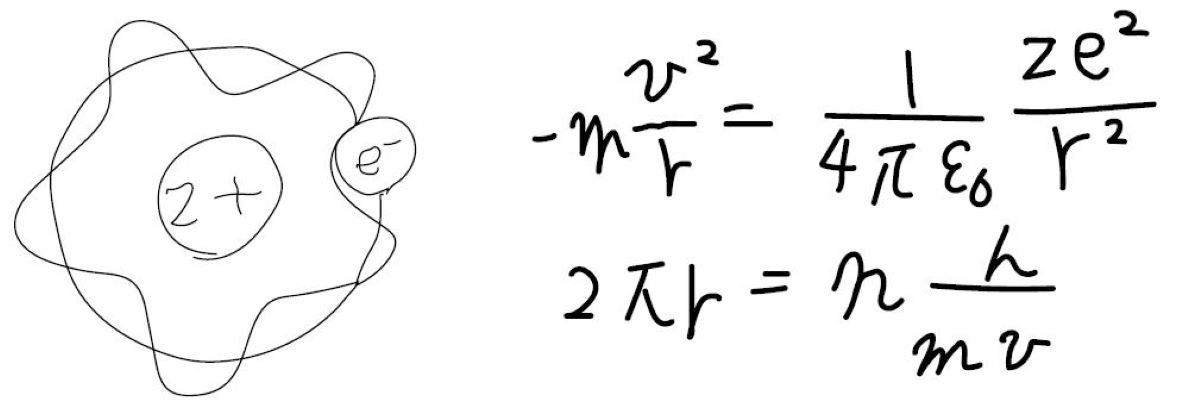
上式で、\(\displaystyle m\)は電子の質量、\(\displaystyle v\)は速さ、\(\displaystyle r\)は円運動の半径、\(\displaystyle \varepsilon_0\)は真空の誘電率、\(\displaystyle e\)は電気素量、\(\displaystyle z\)は価数であり、静電引力を向心力と考えています。
また、当時電子がどうやら波の性質を持っているらしいということもわかっていたので、一周したときに波の位相がぴったり重なるという条件を設定しました。
\(\displaystyle h\)はプランク定数で、これを運動量\(\displaystyle mv\)で除したものは、電子のド・ブロイ波長となります。
電子が1周回ったときに、もとの位相と一致するとし、円周の長さが波長の自然数倍であると考えます。
この連立方程式を解くことで電子の回転半径とエネルギー順位が計算できます。
このモデルは、電子殻のエネルギーがとびとびの値であることを説明し、さらに水素様原子のエネルギー順位を精度よく予想したことから、現在も高校で教えられるほど支持されています。
しかし実際には、このモデルは否定されています。
その理由としては、まず、等速円運動は平面上の運動であるので、このモデルが正しければ、原子は二次元的な広がりしかないことになってしまいます。
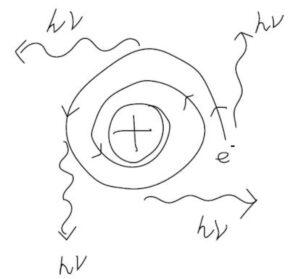
また、制動放射を考えると、電子は絶えず向心力を受けているので、接線方向に電磁波を出しながら回転し続けることになります。
そうすると、放出した電磁波に相当するエネルギーを失いながら回転するので、だんだん回転半径が小さくなっていき、いずれは原子核と衝突するということになります。
つまり、ボーアのモデルで原子は不安定な状態であると予測されます。
実際には、水素など安定な原子の存在があるので、このモデルは現実と矛盾しているということになりました。
実際の原子はどうなっている?
それでは最後、ボーアのモデルの何がいけなかったのかという話になるのですが、それは原子という小さな世界のことを古典力学で計算しようとしたことでした。
今では、こういった小さな世界は量子力学という別の力学法則に従うことがわかっており、原子の安定性もそちらで説明されています。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!