こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(Flory-Huggins)
それでは内容に入っていきます!
正則溶液
まず、溶質が低分子の場合についておさらいしましょう。
こちらの記事の内容です。

2成分\(\rm{A}\)と\(\rm{B}\)の混合系で、分子間にはロンドン分散力のみがはたらくとした正則溶液では、混合エントロピー\(\Delta_\rm{mix}\)\( S\)が\(-nR(x_\rm{A}\)\(\ln{x_\rm{A}}\)\(+x_\rm{B}\)\(\ln{x_\rm{B}})\)と書けます。

そして、混合エンタルピー\(\Delta_\rm{mix}\)\( H=n\xi RTx_\rm{A}\)\(x_\rm{B}\)となります。
ここで、\(n\)は\(\rm{A}\)と\(\rm{B}\)の物質量の和、\(R\)は気体定数、\(x_\rm{A}\)と\(x_\rm{B}\)はそれぞれの成分のモル分率を指します。
\(T\)が絶対温度で、\(\xi\)は分子間相互作用を考慮するための無次元量です。
これらより、混合ギブズエネルギーは\(nRT(\xi x_\rm{A}\)\(x_\rm{B}\)\(+x_\rm{A}\)\(\ln{x_\rm{A}}\)\(+x_\rm{B}\)\(\ln{x_\rm{B}})\)となります。
これは前回の練習問題の答えですが、\(\xi\)が\(2\)より大きいときには、混合ギブズエネルギーが双極小型のグラフとなり、中間の濃度域で相分離が起こることになります。
また、両端における混合エントロピーの傾きが無限大となるため、両端には混合ギブズエネルギーが負となる領域が必ず存在することになります。

つまり、水と油のように一般的には混ざり合わないと思われている組み合わせでも、少量であれば混ざるということです。
格子モデル
ここから、新しい内容です。
エンタルピーやエントロピーを考える際の簡単な粗視化モデルとして、格子モデルを使ってみます。
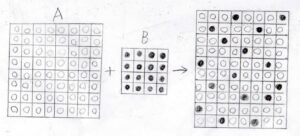
モデルでは、溶質分子の体積分だけ溶液の体積も増加したと考えます。
温度、圧力、体積すべてが一定という条件で、混合を考えるため、ギブズエネルギー変化とヘルムホルツエネルギー変化は、等しい値になります。
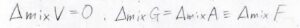
ここでは、まとめて自由エネルギー\(F\)と書くことにしておきます。
2成分の混合により、このようにランダムな配置をとることを考えます。
ここに書けるぐらいの格子だけでアボガドロ数程度の分子の挙動を理解したいので、巨視的には溶液は均一であることを仮定し、溶液全体はこの格子を連続して繋げたものと考えます。
ここからは、モル分率の代わりに溶質の体積分率\(\phi\)を用いることにします。

そして、相互作用のパラメータを\(\chi\)として、混合エンタルピーを\(n \chi RT \phi (1-\phi)\)と表します。
Flory-Huggins理論
溶質が高分子の場合は、下図のように溶質が繋がった系を考えることになります。
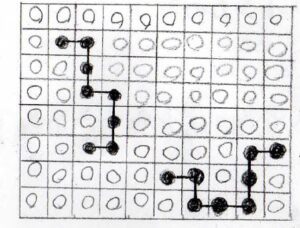
今回のテーマになっているFlory-Huggins理論とは、このような格子モデルから高分子溶液の熱力学量を考える理論です。
低分子から高分子になると、先ほどの低分子の場合に比べて、溶媒分子同士が隣接しやすくなっていることがわかります。
また当たり前ですが、高分子が長いほど、すなわちセグメント数\(N\)が大きいほど、セグメント同士が接近する確率が高くなります。
すべての場合の数を\(W\)とすると、それはこのような式になります。
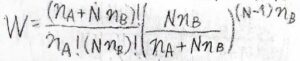
\(\displaystyle \frac{(n_\rm{A}+\mathit{Nn}_B)!}{n_\rm{A}!(\mathit{Nn}_B)!}\)の部分は、溶質が低分子のときの場合の数です。
ただし、高分子ではセグメント同士が繋がれているという制約により、とりうる場合の数が少なくなります。
\(\displaystyle [\frac{Nn_\rm{B}}{(n_\rm{A}+\mathit{Nn}_B)}]^{(N-1)n_\rm{B}}\)の部分が、その制約を表しています。
ボルツマンの式よりエントロピーは、ボルツマン定数\(k_\rm{B}\)を使って、\(k_\rm{B}\)\(\ln{W}\)と表されることから、混合エントロピーが求められます。
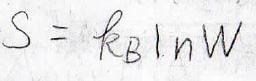
ボルツマンの式の導出過程は、こちらを参照ください。

先ほど、混合エンタルピーを溶質の体積分率を使って表すことにしたので、以上より自由エネルギー変化\(\Delta_\rm{mix}\)\( F\)が求められます。
その値は、\(RT(n_\rm{A}\)\(+Nn_\rm{B}\)\(\displaystyle )[\chi \phi(1-\phi)+(1-\phi)\ln{(1-\phi)}+\frac{\phi}{N}\ln{\phi}]\)となります。
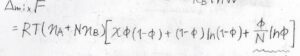
溶質が低分子のときと異なるのは、かっこの中の第三項が\(\phi \ln{\phi}\)ではなく、\(\displaystyle \frac{\phi}{N}\ln{\phi}\)となっていることです。
セグメント同士は繋がっているため、ばらばらになれず、混合エントロピーが小さくなります。
溶媒\(\rm{A}\)、溶質\(\rm{B}\)の化学ポテンシャルもこのように表されます。

いずれもかっこの中の第三項が、溶質が高分子であることによって現れたものです。
もちろん、\(N=1\)を代入したときには、すべて低分子の式と一致しますので、確かめてみてください。
上の式をグラフに書くと、このようになります。
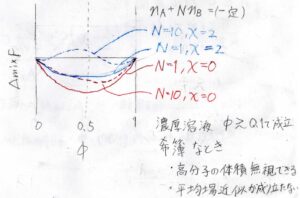
赤で書かれたのが\(\chi=0\)、すなわち異種セグメント間で斥力と引力がつりあっている場合を表し、青で書かれたのが\(\chi=2\)、すなわち異種セグメント間で斥力が優勢となっている場合を表しています。
実線が\(N=1\)の低分子を表し、点線が\(N=10\)の高分子を表しています。
まず、\(\chi=0\)のときで比較すると、低分子のときは\(\phi=0.5\)を中心に左右対称なグラフになっているのに対し、高分子では非対称になります。
そして\(\chi=2\)のとき、低分子では双極小型にならない境界のところですが、高分子ではすでに双極小型となっており、相分離も起こります。
実際の高分子溶液と比較すると、\(\phi\)がだいたい\(0.1\)よりも大きい濃厚溶液でこのような挙動が見られるようになります。
これよりも低濃度のときには、まず溶質の体積があまり効いてこないという点と不均一性が大きく平均場近似が成り立たないという点で、格子モデルが合わなくなります。
ポリマーブレンド
さらに、溶媒と呼んでいた成分も高分子にして、高分子同士の混合物についても、同様に自由エネルギー変化を考えることができます。
高分子同士の混合物のことは、ポリマーブレンドと呼びます。
高分子同士で会合が起こらないとき、2成分の混合による自由エネルギー変化\(\Delta_\rm{mix}\)\( F\)は、このように表されます。
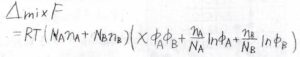
両方の成分について、対数の前の係数をセグメント数で割ることになります。
浸透圧
最後、前回も少し説明した、高分子溶液の浸透圧について、Flory-Hugginsの理論から考えてみます。
溶媒の化学ポテンシャルが混合により減少した値を溶媒の体積で割った値が浸透圧\(\Pi\)になります。
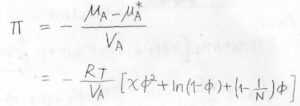
したがって、\(\displaystyle \Pi=-\frac{RT}{V_\rm{A}}[\chi \phi^2+\ln{(1-\phi)}+(1-\frac{1}{N})\phi]\)と求められます。
ここで、体積分率\(\phi\)を質量濃度\(c\)と高分子の部分比容\(\bar{v}\)の積として、書くことにします。
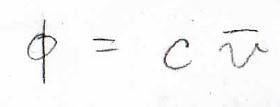
そうすると、自然対数のテイラー展開を考えることで、\(\chi\)と\(\bar{v}\)を用いて浸透圧のビリアル係数を表すことができます。

横軸に\(c\)、縦軸に\(\displaystyle \frac{\Pi}{cRT}\)を書いて、低濃度域のデータを直線に近似したときの傾きが第二ビリアル係数で、それは\(\displaystyle \frac{\bar{v}^2}{V_\rm{A}}(\frac{1}{2}-\chi)\)と表されます。
ここから、相互作用パラメータ\(\chi\)への依存性が説明されます。
ただし、注意も必要で、実際の第二ビリアル係数はセグメント数にも依存しますが、Flory-Huggins理論ではこれを説明できません。
これは平均場近似を使っているためです。
ここについては、単一接触近似という別の方法で近似を行うことで、セグメント数依存性が説明されることになります。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!