こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(Gough-Joule)
グー-ジュール(Gough-Joule)効果
まず、圧力\(p\)を一定条件下で、エントロピー\(S\)を絶対温度\(T\)とゴムの長さ\(L\)の二変数関数として考えます。
その全微分\(\rm{d}\)\(S\)は、このように書けます。
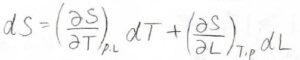
ここで、定圧熱容量の定義\(\displaystyle C_p=(\frac{\partial H}{\partial T})_{p, L}\)より、\(\displaystyle (\frac{\partial S}{\partial T})_{p, L}=\frac{C_p}{T}\)と書けます。
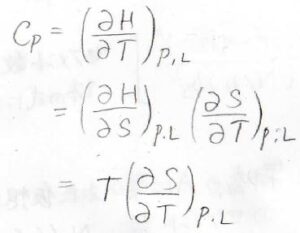
ここで、\(H\)はエンタルピーです。
また、マクスウェルの関係式を考えると、\(\displaystyle (\frac{\partial S}{\partial L})_{T, p}=-(\frac{\partial f}{\partial T})_{p, L}\)となります。
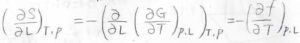
したがって、\(\rm{d}\)\(\displaystyle S=\frac{C_p}{T}\rm{d}\)\(\displaystyle T-(\frac{\partial f}{\partial T})_{p, L}\rm{d}\)\(L\)と変形できます。
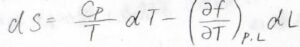
ここで、ゴムを伸ばしたときの温度変化を考えるのですが、瞬間的に変形が起こったため、その間に熱のやり取りは起こらなかったと仮定します。
すると、可逆系であるゴムではエントロピー一定となるので、この式を整理すると、\(\displaystyle (\frac{\partial T}{\partial L})_{S, p}=\frac{T}{C_p}(\frac{\partial f}{\partial T})_{p, L}\)となります。
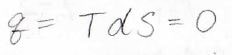
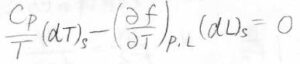
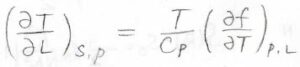
つまり、ゴムを一気に伸ばしたときの温度変化は、長さ一定条件における張力の温度依存性によって決まることになります。
体積\(V\)が伸長により変化することもなく、また温度変化による熱膨張もないものだとすると、エントロピーは\(S_0\)を定数として、下の式で書かれます。
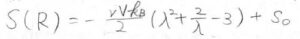
ここでは、アフィン変形を考えています。
\(\nu\)は網目鎖の数密度、\(k_\rm{B}\)はボルツマン定数です。
導出の過程は、こちらを参照してください。
ゴムを引っ張ると、網目鎖のとれる形態が少なくなるため、エントロピーは減少することになり、\(\displaystyle (\frac{\partial f}{\partial T})_{p, L}\)は常に正となります。
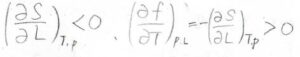
つまり、温度を上げるほどゴムの張力は大きくなり、固いゴムになっていくということです。
金属であれば、エントロピーの寄与がほとんどなく、また熱膨張によりこの符号は負となるため、ゴムは金属と真逆の性質を示すことになります。
そして、\(C_p\)も\(T\)の符号も常に正となるため、\(\displaystyle (\frac{\partial T}{\partial L})_{S, p}\)も常に正となります。
つまり、ゴムを一気に引っ張ると、温度は上昇し、一気に縮めると温度は低下するということになります。
これをグー-ジュール(Gough-Joule)効果と言います。
簡単な実験
実験的に確かめる方法はとても簡単で、おうちでもできるので、ぜひやってみてください。
まず、輪ゴムを1つ用意します。
それを切れない程度に一気に引っ張ります。
そして、引っ張った状態のまますぐに、ゴムの中心を鼻の下か唇に当ててください。
鼻の下や唇は、感覚神経が集中しているので、わずかな温度変化でも感じとりやすい部位です。
実際に、少し熱くなっていることがわかるかと思います。
それから、ゴムを一気に縮めて、もう一度鼻の下か唇に当ててください。
すると、今度は逆に少し冷たくなります。
熱弾性的反転
ここからは難しい話になるのですが、補足として熱膨張の効果も考えていきます。
実は、温度が低くて、伸長度も約\(10\%\)までと小さいときには、エントロピーよりも熱膨張の影響が大きくなることで、\(\displaystyle (\frac{\partial f}{\partial T})_{p, L}\)の符号がマイナスになることがあります。
この反転現象を熱弾性的反転と言います。
その反転が起こる伸長比は、次のように求めることができます。
まず、\(x\)軸方向への一軸伸長試験をするものとして、\(\lambda_x=\lambda\)とします。
張力を温度、圧力、伸長比の三変数関数とすると、その全微分はこのように書けます。
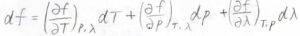
ここで、温度とゴムの長さを一定として両辺を\(\rm{d}\)\(T\)で割ると、\(\displaystyle (\frac{\partial f}{\partial T})_{p, L}=(\frac{\partial f}{\partial T})_{p, \lambda}+(\frac{\partial f}{\partial \lambda})_{T, p}(\frac{\partial \lambda}{\partial T})_{p, L}\)となります。
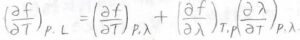
熱膨張はあっても、伸長によって体積が変わることはないとして、さらにエンタルピーが張力に寄与せず、アフィン変形したときには、\(\displaystyle (\frac{\partial f}{\partial T})_{p, \lambda}=\frac{\nu Vk_\rm{B}}{L_0}(\lambda-\frac{1}{\lambda^2})\)となります。
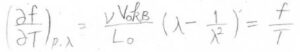
ここで、\(L_0\)はゴムの自然長ですが、これが温度に依存する部分になることに注意してください。
そして、この式は\(\displaystyle \frac{f}{T}\)とも書くことができます。
\(\displaystyle (\frac{\partial f}{\partial \lambda})_{T, p}=\frac{\nu Vk_\rm{B}\mathit{T}}{L_0}(1+\frac{2}{\lambda^3})\)となるので、これは\(\displaystyle \frac{1+2/\lambda^3}{\lambda-1/\lambda^2}f\)と表すことができます。
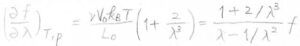
\(\displaystyle (\frac{\partial \lambda}{\partial T})_{p, L}\)については、まず体積膨張率を\(\alpha_V\)とすると、変形前の体積\(V_0\)を\(L_0^3\)と表して、\(\displaystyle \alpha_V=\frac{3}{L_0}(\frac{\partial L_0}{\partial T})_{p, L}\)となります。
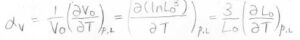
したがって、\(\displaystyle (\frac{\partial \lambda}{\partial T})_{p, L}=-\frac{1}{3}\lambda \alpha_V\)と書き換えられます。
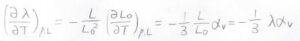
以上のことをまとめると、\(\displaystyle (\frac{\partial f}{\partial T})_{p, L}=\frac{f}{T}-\frac{1+2/\lambda^3}{3(1-1/\lambda^3)}\alpha_V f\)となります。
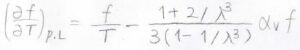
熱弾性的反転が起こるのは、この値が\(0\)になるときなので、このときの\(\lambda\)を求めると、温度が十分に低いときには、\(\displaystyle 1+\frac{\alpha_V T}{3}\)と近似されます。
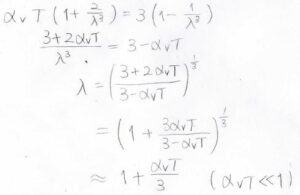
一般的なゴムでは\(\alpha_V=\)\(0.0005\)~\(0.001\ \rm{K}\)\(^{-1}\)程度になるため、伸長度で言えば常温で\(\lambda-1=5\)~\(10\%\)くらいで熱弾性的反転が起こることになります。
微分方程式を解けば、圧力と長さを一定にして張力の温度依存性を求めることができます。
ここでは、体積膨張率\(\alpha_V\)の温度依存性は無視できるものとします。
まず、伸長比\(\lambda\)は温度の関数として、\(\displaystyle \lambda_0\exp{(-\frac{1}{3}\alpha_V T)}\)となります。
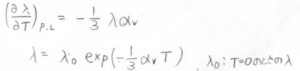
ここで、\(\lambda_0\)は絶対零度における伸長比です。
これを張力の微分方程式に入れて解くと、最終的に\(\displaystyle f=CT[\lambda_0^3\exp{(-\frac{1}{3}\alpha_V T)}-\exp{(\frac{2}{3}\alpha_V T)}]\)となります。

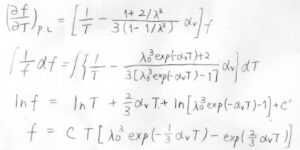
ここで、\(C\)は絶対零度での長さといまの長さ、そして網目鎖の本数に依存し、温度には依存しない値です。
熱膨張がないとき、すなわち\(\alpha_V=0\)のとき、\(\displaystyle f\)は\(\displaystyle \lambda_0-\frac{1}{\lambda_0^2}\)に比例するはずなので、\(C\)は\(\lambda_0^2\)に比例します。
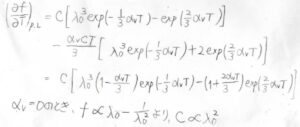
そして、\(\displaystyle (\frac{\partial f}{\partial T})_{p, L}=C[\lambda_0^3(1-\frac{1}{3}\alpha_VT)\exp{(-\frac{1}{3}\alpha_V T)}-(1+\frac{2}{3}\alpha_V T)\exp{(\frac{2}{3}\alpha_V T)}]\)となります。
以上の結果をグラフに書くと、下のようになります。
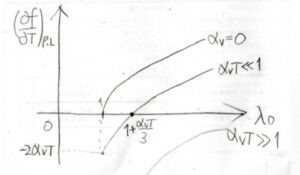
ここでは、圧力と長さを一定としており、熱分解とガラス転移を考えていません。
また、\(\alpha_V\)の温度依存性も無視しており、張力のエンタルピー成分もないものとしています。
上のグラフは、温度を固定して横軸を\(\lambda_0\)、縦軸を\(\displaystyle (\frac{\partial f}{\partial T})_{p, L}\)としたものです。
まず、\(\alpha_V=0\)というのは熱膨張がないときです。
このときはどんな温度でも同じ曲線になります。
そして、熱膨張があり、さらに温度が十分に低いときには、小さい変形量のときにだけ、張力が温度に対して負の依存性をもつことになります。
そして、実際には熱分解するのであり得ませんが、とても高い温度にすると、張力は常に負になります。
そして、温度に対して張力を書くと、下のグラフのようになります。
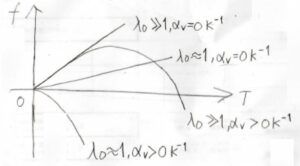
もとの変形量が小さいときには、熱膨張ですぐにゴムがたるんだような状態になるので、それがマイナスの張力として現れているイメージです。
どれだけ引っ張っていたとしても、無限に熱膨張できる場合には、どこかでたるんできて、張力が減衰していきます。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!