こんにちは!
今回も化学のための数学の続きをやっていきます。
今日のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(permutation)
置換とは
まず、置換がどんなものかというと、\(n\)個の整数からなる集合から自身への1対1写像のことを言います。
例えば、\(1\)、\(2\)、\(3\)が並んでいる中で\(1\)と\(2\)を入れ替えるという操作を行うことを置換と言い、下のような形で表します。
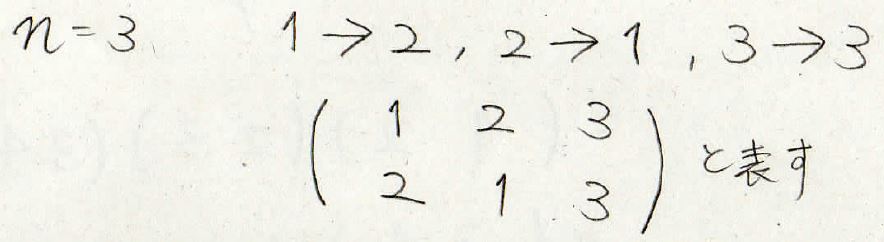
2段になっている上側の行には\(1\)、\(2\)、\(3\)と数字を書きます。
そして、下の行には入れ替えを行った後の数字の並びを書きます。
この例であれば、\(1\)と\(2\)を入れ替えるという操作をしているので、\(1\)の下に\(2\)、\(2\)の下に\(1\)という形になります。
これを一般化すると、\(1\)が移される先が\(k_1\)、\(2\)が移される先が\(k_2\)と書けます。
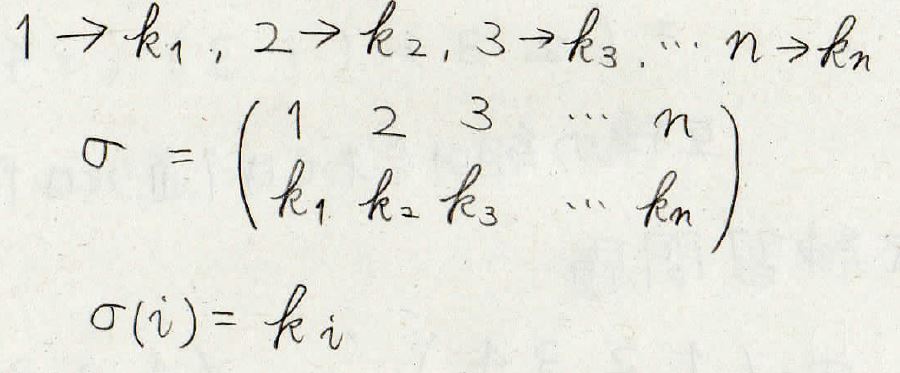
この置換を\(\sigma\)として表すことにすると、\(i\)が移される先を\(\sigma (i)\)と表現できます。
とりうる置換には数に限りがあり、次数が小さいほど少なくなります。
例えば、\(1\)次の置換はそのままにするという操作しかないため1個しかありません。
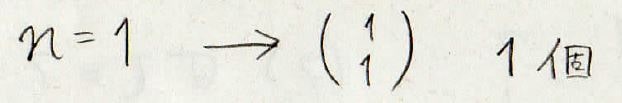
\(2\)次の置換はそのままにするか、\(1\)と\(2\)を入れ替えるかという2個が出てきます。
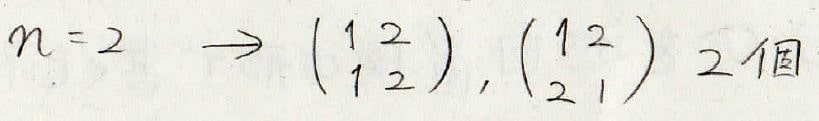
そして\(3\)次の場合は、6個の置換が存在します。
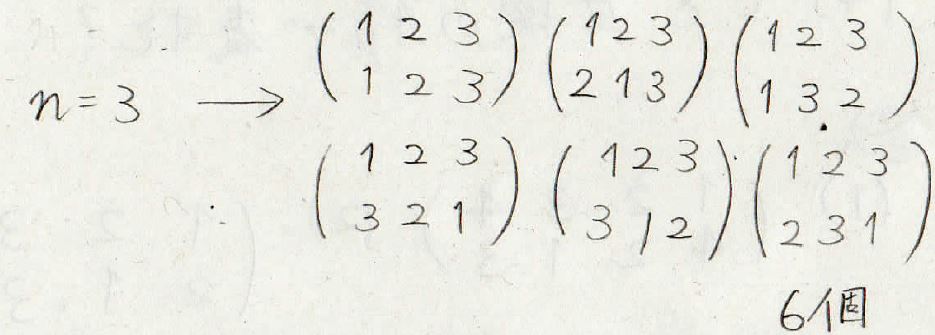
とりうる置換の個数は、その次数の階乗になります。
置換の掛け算
ここからは、置換のかけ算をどう考えるのかという話をします。
次数が同じ2つの置換\(\sigma\)と\(\tau\)について、\(\sigma \tau\)の\(i\)が移される先は\(\sigma (\tau (i))\)になります。

実際の例でやってみると、下のようになります。
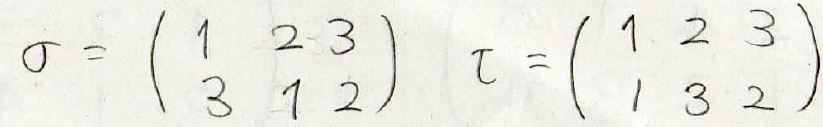
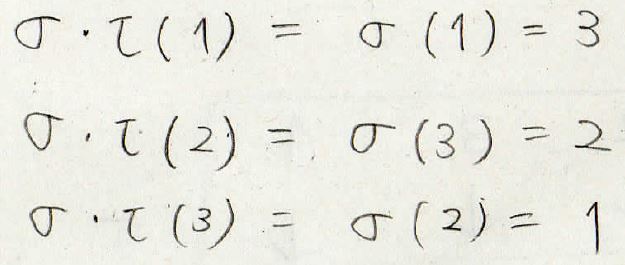
\(\sigma (\tau (1))\)を考える際には、まず\(\tau (1)\)を見ます。
すると\(1\)になるので、今度は\(\sigma (1)\)を見て、\(3\)になります。
\(\sigma (\tau (2))\)については、まず\(\tau (2)\)が\(3\)なので\(\sigma (3)\)を見て、\(2\)となります。
そして、\(\sigma (\tau (3))\)は余った\(1\)になります。
単位置換
続いて、単位置換というものについてお話しします。
言葉で説明すると、そのままにしておくという操作のことです。
すなわち、上の段の数字と下の段の数字がすべて同じになっている置換が単位置換となります。

そして、ある置換に対してかけ算をすることで単位置換になる置換のことを逆置換といいます。
逆置換とのかけ算では、順番を交換することもできます。
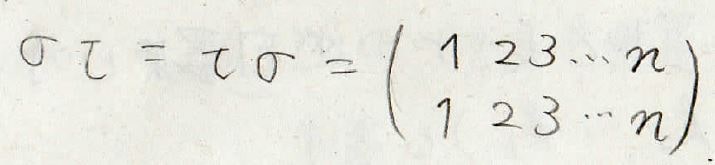
一般的に、このような置換の積は交換できないので知っておいてください。
試しに、先ほど出てきた\(\sigma\)と\(\tau\)を使って\(\tau \sigma\)を出してみると、\(\sigma \tau\)と一致していません。
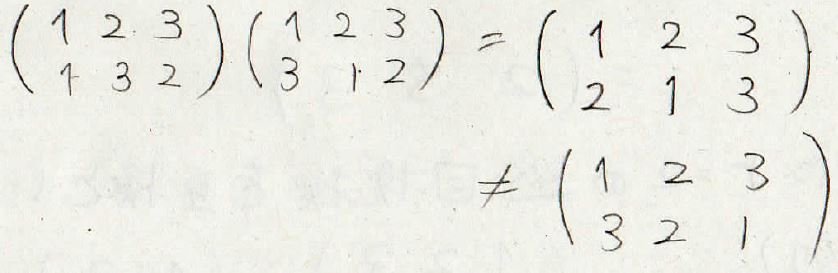
逆置換の求め方
逆置換は次のようにして求めます。
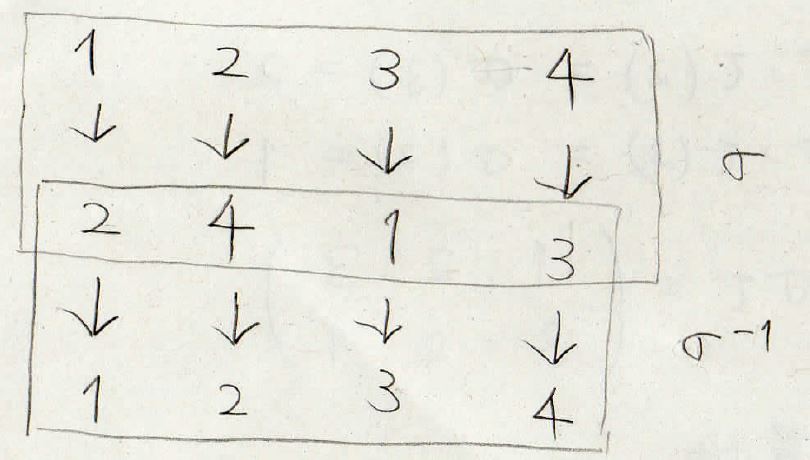
まず、\(\sigma\)の上の段と下の段を入れ替えて書きます。

そのあと、上の段が\(1\)、\(2\)、\(3\)、\(4\)と順番になるように並び替えるだけです。
模式的に書けば、こちらのようになります。
巡回置換
続いて、巡回置換についてお話しします。
巡回置換とは、ある値から始まり移った先の値を見て、その値が今度どこに移るのかというのが一周するまでつなげたものです。
そこで出てこなかった値は固定して、出てきた値だけを順番に並べたものが巡回置換となります。
そのとき出てきた値の個数を長さと言います。
例えば、\(\sigma\)が下の置換だったとします。
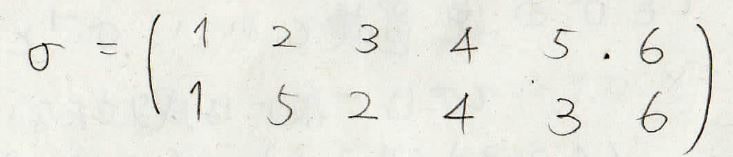
ここで、\(1\)、\(4\)、\(6\)は上下が同じで固定されています。
違う値へ移っている中で、まず\(2\)に注目してみると、\(2\)は\(5\)に移されています。
今度は\(5\)の移り先に着目すると、\(5\)は\(3\)に移っています。
そして、また\(3\)に着目してみると、\(3\)の移り先は\(2\)になっており、これで一周しました。
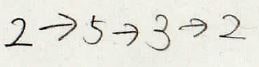
そして、この場合には出てきた値を順番に並べて\((2\ 5\ 3)\)と表記します。
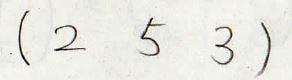
これが巡回置換です。
この場合の長さは\(3\)になります。
互換
特に長さが\(2\)の巡回置換のことは、互換と呼ばれます。
長さが\(2\)ということは、単純に2つの値を入れ替える操作になります。
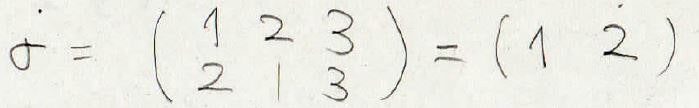
任意の置換は、互換の積という形で表現することができます。
例えば、この\(\sigma\)を互換の積の形にすると\((1\ 2)(2\ 3)(3\ 4)\)となります。
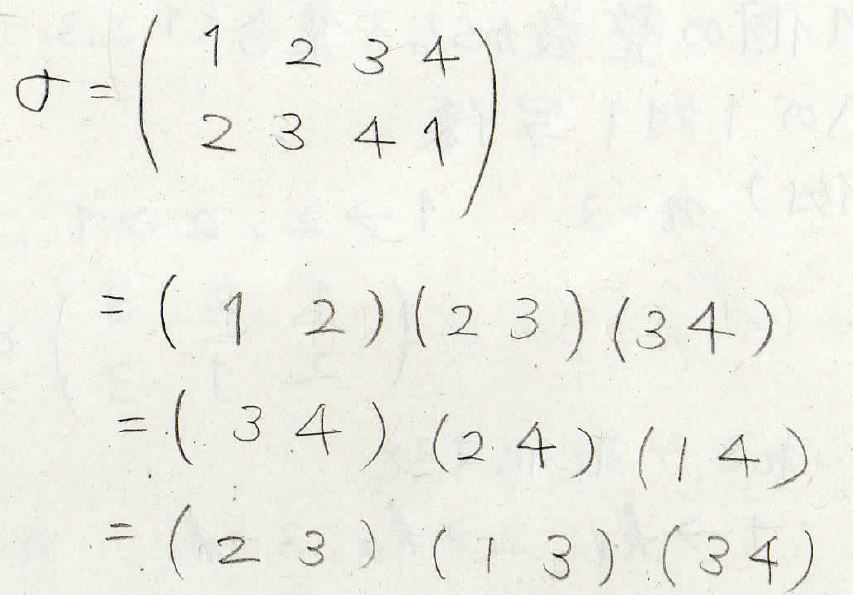
また、どこから入れ替えてもいいので、\((3\ 4)(2\ 4)(1\ 4)\)や\((2\ 3)(1\ 3)(3\ 4)\)なども\(\sigma\)と同じ意味になります。
このように、互換の積としての書き換えは、1通りとは限りません。
練習問題
はい、それでは本題は以上ですので練習問題をやってみましょう!
\(\sigma\)と\(\tau\)を下のように与えられるとき、\(\sigma ^{-1}\)、\(\sigma \tau\)、\(\sigma\)の巡回置換としての表記、\(\tau\)の互換の積としての表記をそれぞれ求めてください。

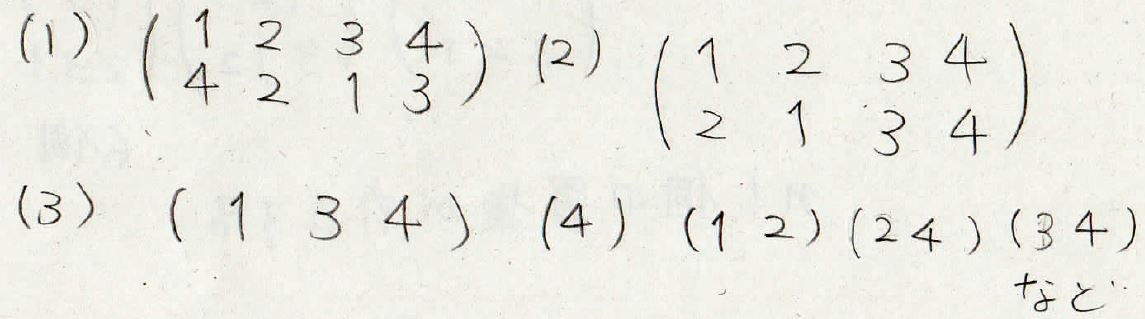
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




