こんにちは!
それでは今回も化学のお話やっていきます。
今回のテーマはこちら!
それでは内容に入っていきます!
基本的な考え方のおさらい
まずはヒュッケル法の基本的な考え方をおさらいします。
ヒュッケル法は\(\displaystyle \pi\)電子のエネルギー準位を簡易的に求める方法です。

そのために色々な近似を入れるわけですが、その中でも特徴的なのが\(ヒュッケル近似\)で、隣接する炭素以外の影響をまったく考えないとします。
この近似を入れると、\(0\)と\(1\)と\(-x\)しか出てこない行列式を解くことでエネルギー準位と分子軌道の形を求めることができます。
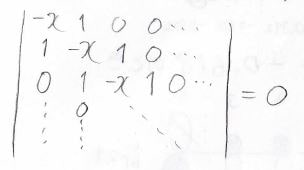
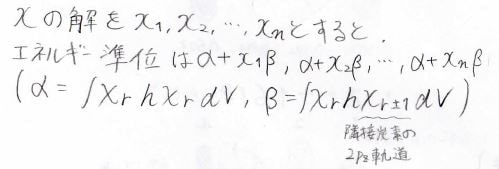
詳しくは前回の記事を見てください。

実際に計算してみよう!
ここからが新しい内容です。
実際にいくつかの化合物について計算してみましょう!
エチレン
まずは、\(\displaystyle \pi\)電子共役系ではありませんがエチレンについて考えてみます。
解くべき行列式はこんな感じです。
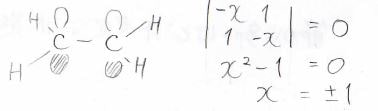
\(x=\pm1\)となり、二重結合のエネルギー準位は\(\alpha\pm\beta\)になります。
ここで、\(\alpha\)と\(\beta\)はエネルギーの安定化を表すものであり、負の値となるため、\(\alpha+\beta\)の方が低エネルギー側になります。

電子2個を低エネルギー側に入れた基底状態では、全体のエネルギー\(E\)は\(2\alpha+2\beta\)となります。
ここで\(2\alpha\)の部分は、炭素原子2個がもっていたエネルギーで、\(2\beta\)の部分が二重結合を形成したことによる安定化を表します。
そして\(x\)がわかると、各炭素原子の原子軌道が分子全体にどのように寄与しているのかもわかります。
行列式の計算に使った行列は、そもそも永年方程式の係数行列だったので、その連立方程式に\(x\)を代入して、原子軌道の寄与を表す定数\(C\)を求めればいいわけです。
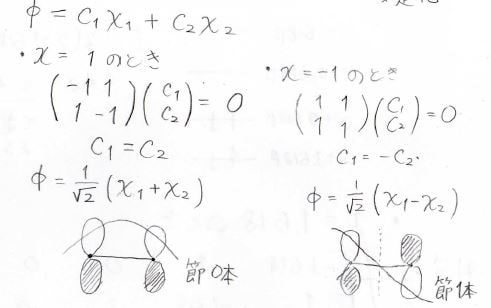
しかし、係数行列が正則行列ではないので、このままだと\(C\)の値は厳密に決まりません。
そこで規格化条件\(C_1^2+C_2^2=1\)を追加します。
波動関数の符号が入れ替わる面のことは節と呼ばれますが、不安定な方には節が1つあって、安定な方には節がありません。
一般的に、節の数が多いほど、その状態は不安定となっていきます。
ブタジエン
それでは次に、ブタジエンについて考えてみましょう。
ブタジエンは炭素原子4個が繋がった直鎖上に2つの二重結合をもつ化合物です。
解くべき方程式は、下記のとおりです。

これを整理すると、\(x\)についての四次方程式が出てきます。
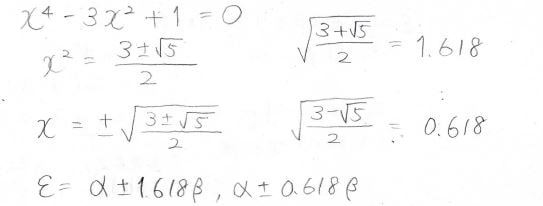
これを解いて、簡単のためにルートを小数で近似すると、\(x\)は\(\pm1.618\)と\(\pm0.618\)となります。
全体のエネルギー\(E\)は下のように計算され、\(4\alpha+4.472\beta\)となります。
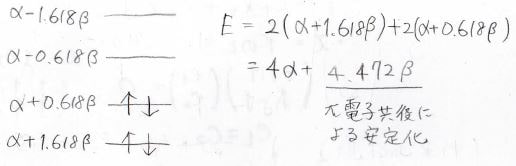
先ほどのエチレンの計算結果より、非局在化していない単純な二重結合1個あたりの安定化は\(2\beta\)であるので、\(\displaystyle \pi\)電子が非局在化したために得られた安定化は\((4.472-2\times2)\beta=0.472\beta\)となります。
したがって、ブタジエンは共鳴安定化していると考えられます。
次に、各状態での炭素原子の寄与計算していきます。
まずは最も安定な\(x=1.618\)のときです。
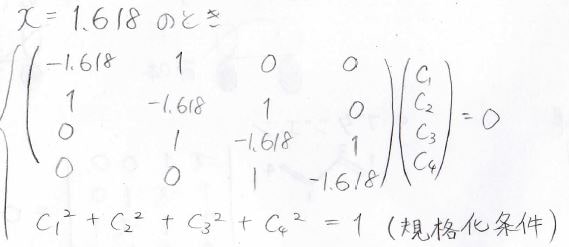
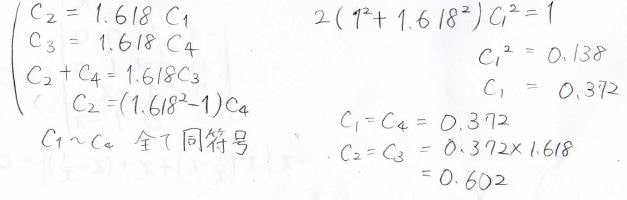
すべての\(C\)の符号が同じになることから、、節がない形だとわかります。
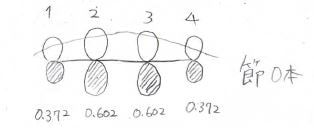
同様の計算をしていくと、各状態の炭素原子の寄与は以下のようになります。
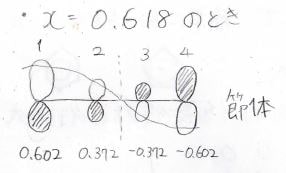
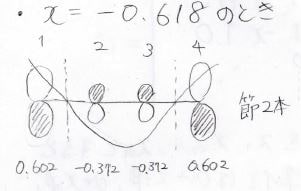

不安定な状態ほど節が増えていきます。
アリルラジカル
続いて、アリルラジカルについて考えていきます。
アリルラジカルとは、アリル位に不対電子をもつ化学種のことです。
アリル位とは、二重結合の1つ隣の炭素の位置を指します。
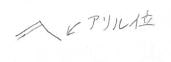
ここでは、下の2-プロぺ二ルラジカルについて計算していきます。

解くべき行列式は、下記のとおりです。
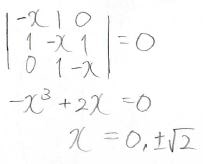
これを解くと、下のようなエネルギー準位になります。

電子の非局在化によって得られる安定化は\(2(\sqrt{2}-1)\beta\)となります。
ここで注目してもらいたいのは、\(x=0\)を解にもっていることです。
この状態では、電子の非局在化によって安定化も不安定化も起こりません。
これが\(\displaystyle \pi\)電子共役系における非結合性軌道ということになります。
また、このように電子対ではなく不対電子が入っている軌道のことはSOMO(Singly Occupied Molecular Orbital)または半占軌道と呼ばれます。
補足
ついでに、SOMOと似た言葉でHOMOとLUMOという用語もあるのでここで紹介しておきます。
HOMOはHighest Occupied Molecular Orbital、日本語で最高被占軌道、つまり電子が占有している軌道の中で最もエネルギーが高い軌道を指します。
LUMOはLowest Unoccupied Molecular Orbital、日本語で最低空軌道、電子が占有していない軌道の中で最もエネルギーが低い軌道を指します。
このHOMOとLUMOは化学反応を理解するうえでとても重要なものになります。
言葉だけでも覚えておいてください。
シクロブタジエン
続いて、シクロブタジエンについて考えてみましょう。
シクロブタジエンとは、四員環で二重結合を2つもった化合物です。
計算過程は以下のとおりです。
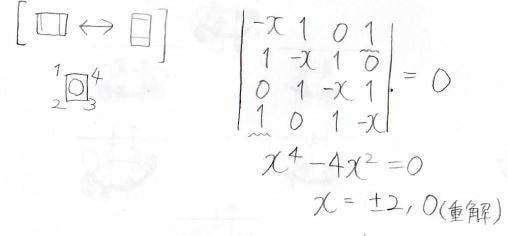
\(x\)は\(0\)を解にもち、さらにそれは二重解になります。
このヒュッケル法の計算において重解は軌道の縮退を指します。
つまりは、下記のイメージです。
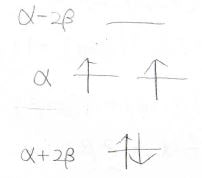
そして、全体のエネルギー\(E\)はこのようにして求められます。
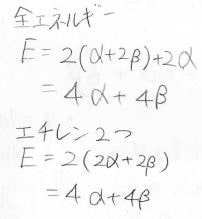
\(\displaystyle \pi\)電子の非局在化によって得られる安定化は\((2\times2-2\times2)\beta=0\)になります。
これはつまり、電子が非局在化しても共鳴安定化が起こらないことを指しています。
さらにHOMOには不対電子が2つあり、ビラジカルになるため不安定化が起こると予想されるため、π電子の非局在化は有利にはたらきません。
その結果、シクロブタジエンでは\(\displaystyle \pi\)電子の非局在かは起こらず、化学平衡になります。
![]()
その交換は共鳴に比べてとても遅く、すべての結合が等価にならないため、長方形型の分子として観測されます。
このように\(\displaystyle \pi\)電子共役系となることで、かえって不安定になってしまう環状化合物は反芳香族と呼ばれます。
ベンゼン
対して、共鳴安定化が起こる環状化合物の代表であるベンゼンについても、ヒュッケル法の計算をやってみましょう。
六次行列式が出てくるため、計算は結構大変になります。
現実的に手計算できる限界はこのベンゼンまでくらいで、これ以上はコンピュータに解かせたほうがよいです。


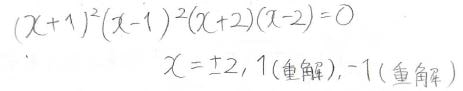
二重解が2組得られます。
エネルギー準位は下記のとおりです。
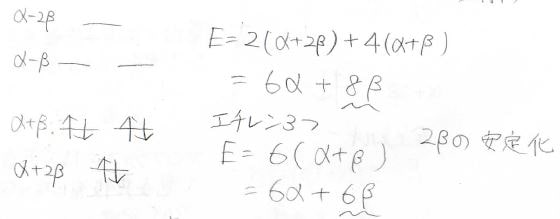
全体のエネルギーを比べてみると、単純な二重結合3つ分よりも\(2\beta\)分だけ安定になっているため、電子の非局在化が起こります。
そして、各状態の原子軌道の寄与は、このように計算されます。

縮退しているときには、永年方程式に規格化条件を入れても厳密解を得られないので、さらに節の通り方から条件を追加します。
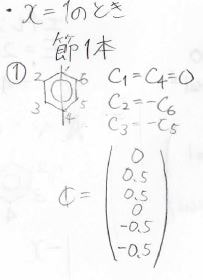


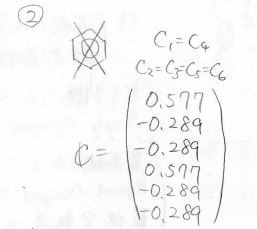
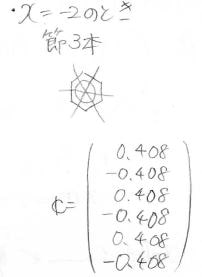
以上を踏まえてベンゼンの分子軌道図を書くと、このようになります。
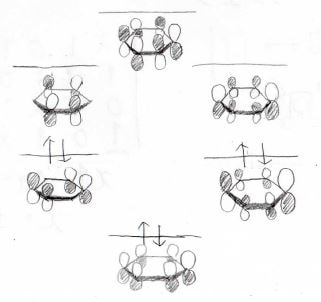
アヌレン(単環状共役ポリエン)
それでは最後、1つの環状で二重結合が複数ある化合物、つまり単環状共役ポリエン、通称アヌレンの計算をしてみましょう。

環状であることから、一周すると同じになります。
そして末端はないため、永年方程式の個々の式はすべて下の形になります。

先述のとおり、炭素数が多くなるほど行列式の次数が多くなっていき、手計算では解くのに多大な時間がかかるようになります。
そうなると行列式を解くのは現実的ではないので、ここでは行列式を解かない方法を紹介します。
それは炭素の原子軌道の寄与を波で考えるということです。
これまでの計算結果について、原子軌道の寄与の大きさを波の変位として見立てると、分子上に波を置くことができます。
オイラーの公式より、複素数に拡張された波は\(\rm{e}\)\(^{-\rm{i}\alpha \mathit{x}}\)で表されます。
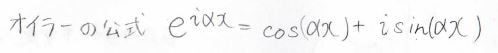
ここでは、\(\mu\)番目の炭素原子の寄与を\(\rm{e}\)\(^{-\rm{i}\mathit{k}\mu}\)として、\(C_\mu\)について変形していきます。
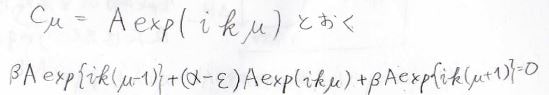
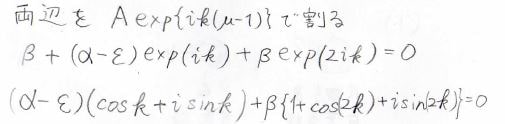
二倍角の定理も使って変形を続けます。

\(\rm{e}\)\(^{-\rm{i}\mathit{k}}\)でくくることができたので、両辺をこれで割ると、\(\varepsilon=\alpha+2\beta\cos{k}\)という式になります。
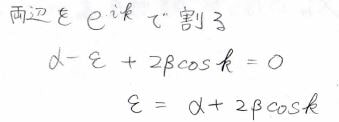
\(\cos{k}\)は\(-1\)以上\(1\)以下の値をとるため、ここから\(\varepsilon\)のとりうる値の範囲がわかります。
![]()
さらに、一周したときの値が同じという条件より、\(k\)を整数\(j\)を使って書けます。

変形の結果、\(\displaystyle \varepsilon=\alpha+2\beta\cos{(\frac{2\pi j}{n}})\)となります。
これは偶関数なので、\(\cos{(-x)}=\cos{x}\)となります。

この式から得られるエネルギー準位の形は、\(n\)が奇数か偶数かによって変わります。
具体的には最もエネルギーが高い軌道が、\(n\)が奇数のときには縮退がなく、\(n\)が偶数のときには2つに縮退した形で現れます。
最もエネルギーが高い軌道以外の形は、奇数偶数どちらも共通していて、最安定の軌道のみ1つ、それ以外は2つに縮退した形をとります。
ヒュッケル則
シクロブタジエンは反芳香族、ベンゼンは芳香族ですが、これには法則があってそれにはこの2つに縮退した軌道がずっと続く形が関係しています。
\(\displaystyle \pi\)電子が\(4n+2\)個のときにはHOMOに電子対が2つあり、共鳴安定化が起こりますが、\(\displaystyle \pi\)電子が\(4n\)個のときにはHOMOには不対電子が2つ並んだビラジカルとなり、共鳴安定化が起こったときのメリットがありません。
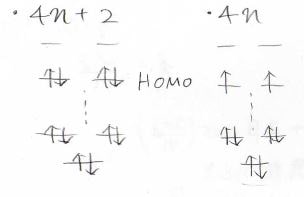
したがって、以下のような予想を立てることができます。

この法則は、ヒュッケル則と呼ばれます。
ただし、このヒュッケルは常に成り立つ法則ではありません。
すべてのアヌレンが芳香族か反芳香族に区別できるわけではなく、シクロペンタジエンのように\(\displaystyle \rm{sp}\)\(^3\)炭素をもっていて、そもそも環全体で共役系になれなかったり、シクロオクタテトラエンのように平面構造が不安定な場合には、どちらでもない非芳香族という分類になります。
炭素原子が窒素原子になった場合でも、同様に考えることができます。

「反」と「非」は英語では”anti“と”non“です。
非芳香族は、何らかの理由でそもそも環全体で\(\displaystyle \pi\)電子共役系になりえないもの、反芳香族は\(\displaystyle \pi\)電子が非局在化しても安定化しないものと認識してください。
練習問題
それでは最後、練習問題を用意したのでやってみましょう。
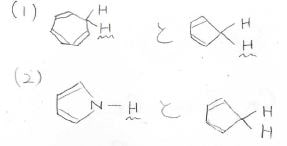
下の2つの化合物の組み合わせで、より酸性度が高い水素原子をもっているのは、どちらでしょうか?
化学反応の熱力学的な変化は、下のポテンシャル図で示されます。
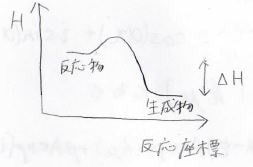
反応物が生成物よりも安定であるときには、その反応が起こりやすいことになります。
それが発熱反応だった場合には、反応熱が大きいほどその反応は起こりやすいです。
すなわち反応物が不安定、もしくは酸解離によって生じるアニオン種のような生成物が安定な場合、反応は起こりやすいです。
(1)
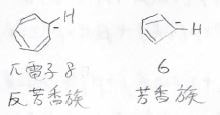
両者でプロトンが外れたときにできるアニオンは、上のようになります。
ヒュッケル則より、\(\displaystyle \pi\)電子が8個のシクロへプタジエニルアニオンは反芳香族、\(\displaystyle \pi\)電子が6個のシクロペンタジエニルアニオンは芳香族となるため、後者の方が熱力学的に安定であり、シクロペンタジエンの方が酸性度が高いことになります。
(2)

酸解離する前、左側のピロールは\(\displaystyle \pi\)電子が6個あるため、芳香族ですでに安定です。
ここからわざわざプロトンが外れて不安定なアニオンになるとは考えにくいため、右側のシクロペンタジエンがより強い酸になります。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!