こんにちは!
今日は数学の話をしていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(sign function)
では参りましょう!
前回のおさらい
まず、これは前回の復習ですが、値の移り先を記述したものを置換と言って、2行の行列のような形で表現します。
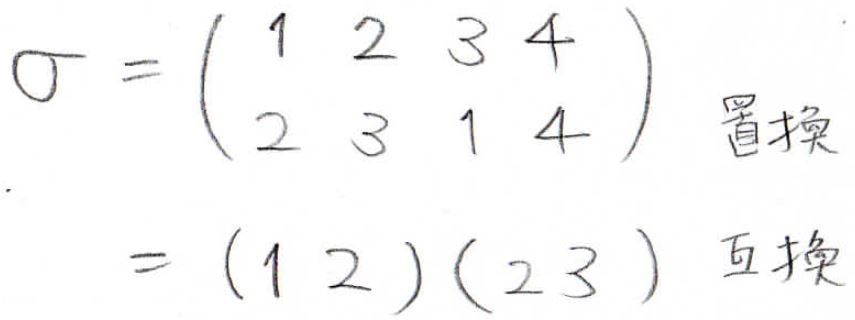
そして、2つの値を入れ替えるという最も単純な操作のことは互換と言い、入れ替える2つの値を書いて表します。
どんな置換でも2つの値を入れ替えるという単純な操作を複数回行うことで表現できるため、置換は互換の積として表すことができます。
詳しくは前回の記事をご覧ください。

置換の分類
ここからが新しい内容です。
一般的に、任意の置換を互換で表す方法は、1通りではありません。
どこから入れ替えたとしても、最終的に目的のものにたどり着ければ一緒ということです。
そこで着目するのが、その置換を表現するために最低限必要な互換の個数です。
例えば、先ほども出てきた下の置換、2つの互換を使って書きましたが、これを1つの互換で表現することはできません。
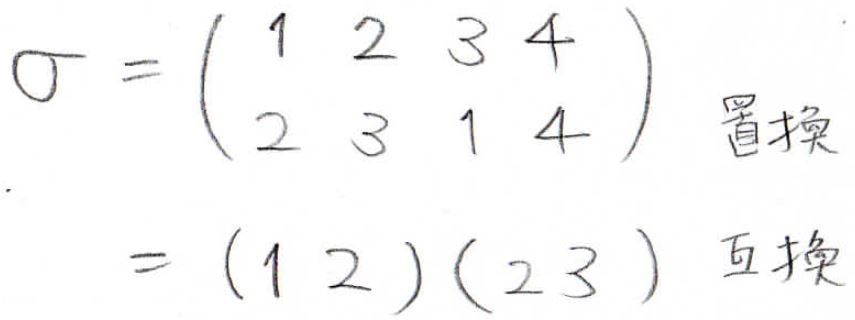
3つの値が変わっているので、少なくとも2回の入れ替えが必要ということになります。
このように、書き換えに必要な互換の個数を考えると、それが偶数個になるか奇数個になるかで置換を分類することができます。
それぞれは、偶置換と奇置換と言います。
例えば、次数が3の置換を見てみると、3つが偶置換で残りの3つが奇置換と分けることができます。

符号関数
ここからは、今回のテーマである符号関数の話に入っていきます。
符号関数は\(\rm{sgn}\)という演算子で表現されます。
置換を\(\sigma\)として、\(\rm{sgn}(\sigma)\)の値は\(\sigma\)が偶置換のときに\(1\)、奇置換のときに\(-1\)となります。
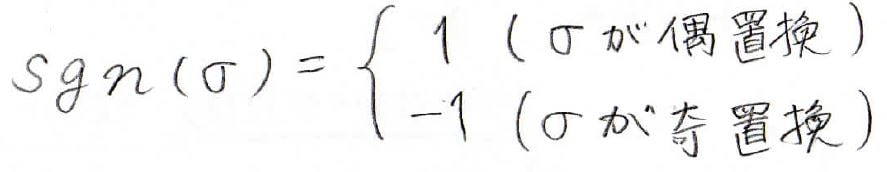
符号関数の定義は、下記のとおりです。
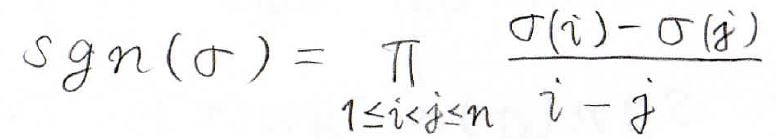
まず、\(\prod\)の記号についてですが、これは\(1\)以上\(n\)以下の整数の組\((i,j)\)について、すべてをかけるという意味です。
ただし、ダブルカウントを避けるために\(j\)は\(i\)より大きいということにします。
次数が\(3\)の置換である\(\sigma\)の符号関数であれば、こちらの式になります。
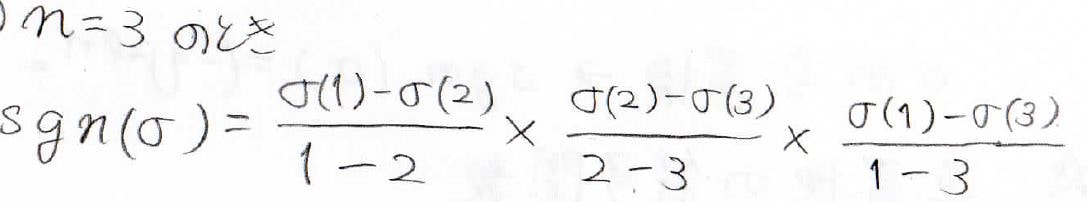
偶置換に対して\(1\)、奇置換に対して\(-1\)を返すことの証明
では、これが本当に偶置換に対して\(1\)、奇置換に対して\(-1\)を返すのかを簡単に証明しておきます。
\(\sigma\)が互換のとき
まず、\(\sigma\)が互換、すなわち、1回だけ2つの値を入れ替えただけのときを考えます。
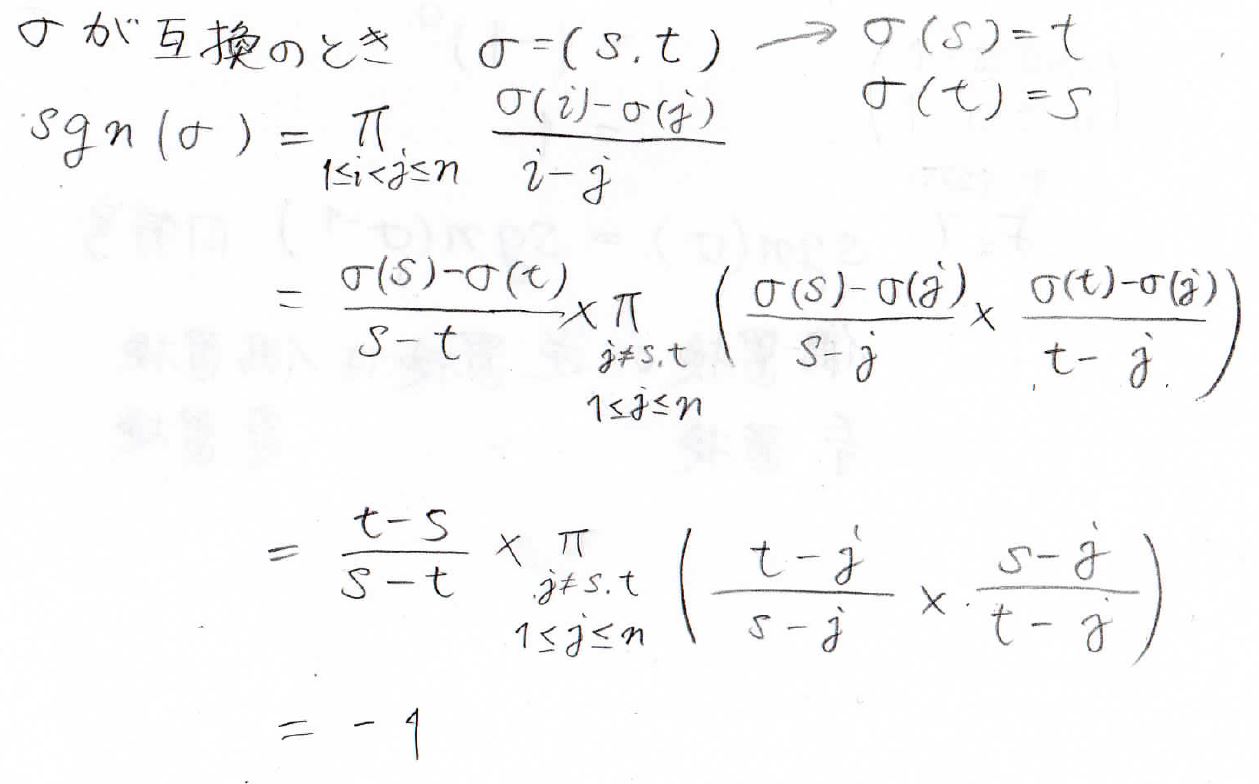
ここでは仮に\((s,t)\)という互換を考えます。
入れ替えたので、\(\sigma (s)=t\)で\(\sigma (t)=s\)になります。
これの符号関数を考えていくのですが、\(s\)と\(t\)以外は値がそのままなので、\(i\)と\(j\)が両方\(s\)か\(t\)でないときには、\(\displaystyle \frac{\sigma (i)-\sigma (j)}{i-j}\)の値は\(1\)になります。
\(1\)を何度かけても変化はないので、結局\(i\)と\(j\)のいずれか、もしくは両方が\(s\)か\(t\)になる場合だけが残ってくることになります。
そしてここで、\(\sigma (s)=t\)と\(\sigma (t)=s\)を代入すると、かっこの中がすべて\(1\)になり、前に出ている部分だけが\(-1\)になるので、互換の符号関数は\(-1\)となります。
置換の積と符号関数の関係
では今度、置換の積について符号関数を考えていきます。
定義のとおりに書いた後、ここで\(\prod\)の中を下のように変形します。
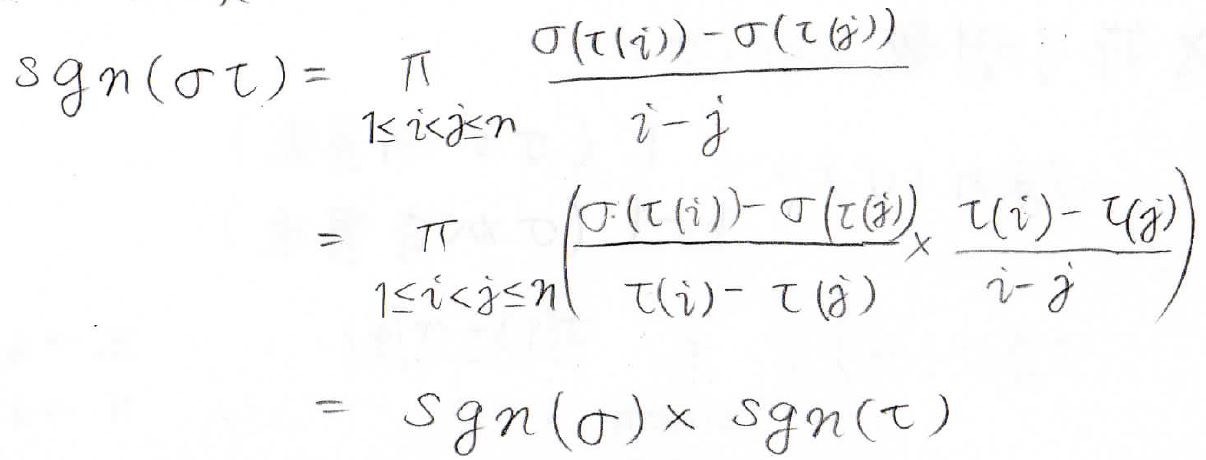
すると最終的には、それぞれの符号関数の積という形に分解できました。
以上のことより、偶置換は\(-1\)を偶数回、奇置換は\(-1\)を奇数回かけることになります。

逆置換の符号関数
逆置換の符号関数はどう書けるのかというのも考えてみます。
\(\sigma \sigma ^{-1}\)は単位置換で、これは互換が0個の偶置換なので、符号関数は\(1\)になります。
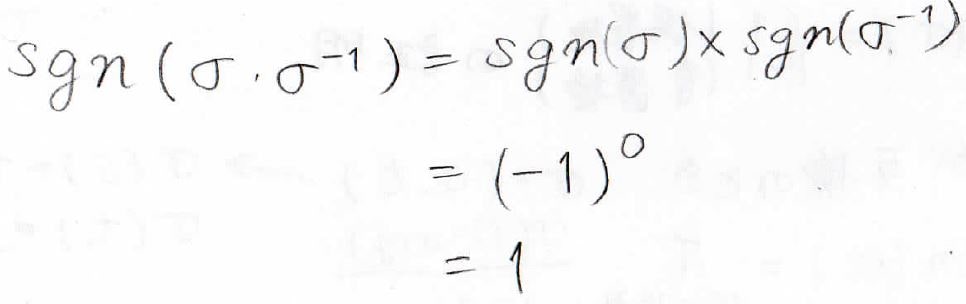
そして置換の積は分解できるので、結局\(\sigma\)の符号関数は\(\sigma ^{-1}\)の符号関数と同符号だとわかります。
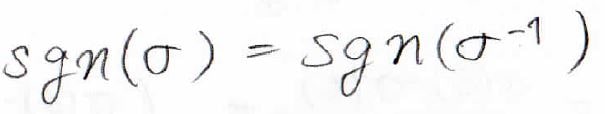
このことから偶置換の逆置換は偶置換、奇置換の逆置換は奇置換だということになります。
練習問題
最後に、練習問題をやってみましょう。
下の置換の符号関数を求めてみてください。
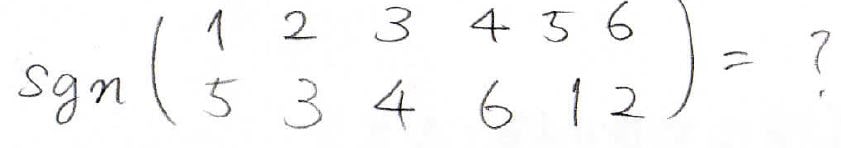
定義に当てはめてもいいですし、互換で書き換えて判断しても構いません。
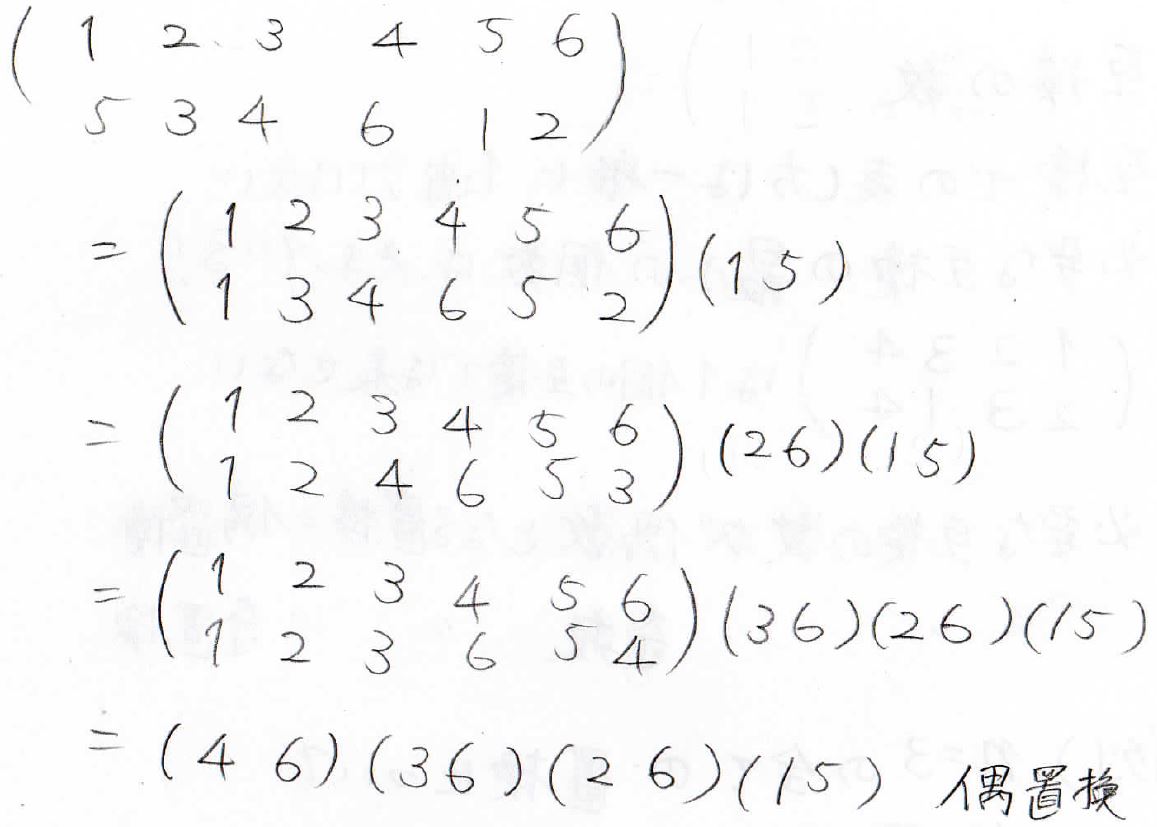
この置換を互換の積で表した場合、\((4\ 6)(3\ 6)(2\ 6)(1\ 5)\)となります。
互換は4つなので、これは偶置換です。
したがって符号関数は\(1\)になります。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




