こんにちは!
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(polar coordinates)
では早速行きましょう!
座標の表し方
座標という言葉はおそらく中学校で習うと思いますが、ある空間の中の特定の位置を示す言葉です。
座標はいくつかの独立なパラメータの組み合わせで表現されますが、そのパラメータの数が次元数となります。
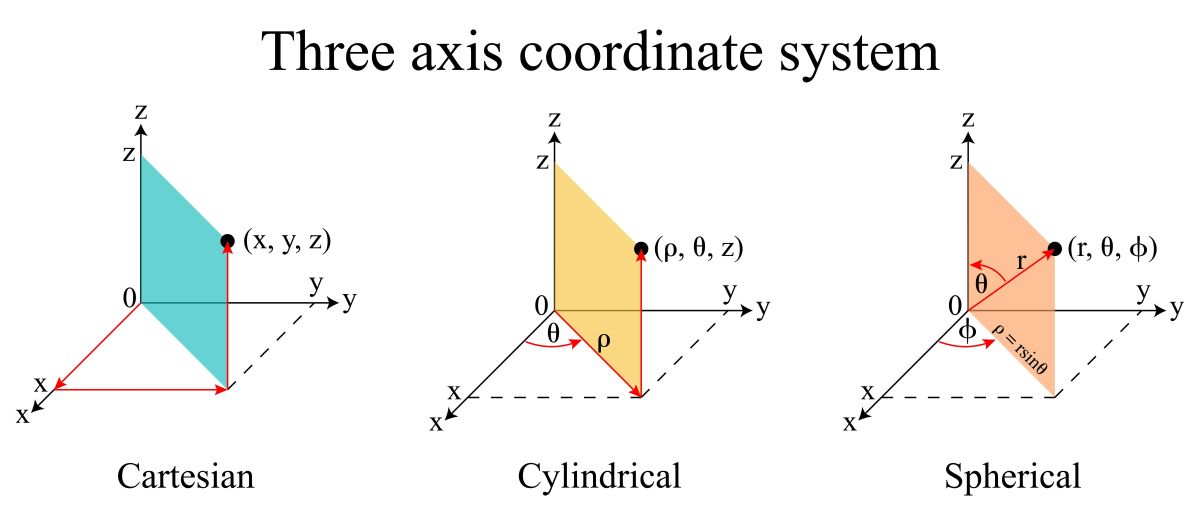
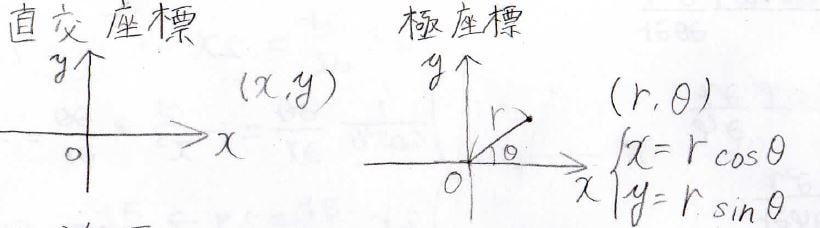
二次元の座標の表し方として、すぐに思いつくのはこんな風に\(x\)軸と\(y\)軸が直角に交わっている形だと思いますが、これだけではなくて、極座標でも表すことができます。
いずれの場合においても独立に変化させられるパラメータは2つです。
\(x\)と\(y\)または、\(r\)と\(\theta\)を決めてあげれば、ある平面内の任意の点を指定することができます。
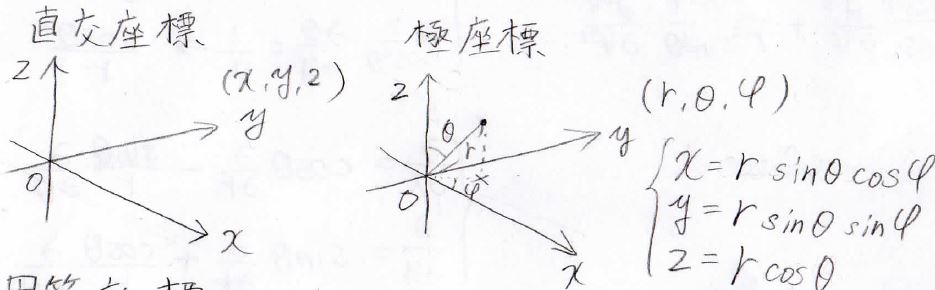
三次元の場合も直交座標、極座標があります。
三次元の極座標は原点からの距離\(r\)と2つの角度パラメータで表現できます。
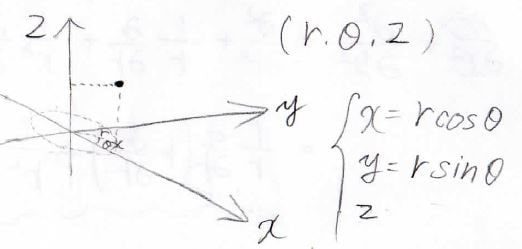
化学ではほとんど出てきませんが、ちょっと変わった形として円筒座標というものもあるので紹介しておきます。
まず、\(xy\)平面の位置を極座標で指定した後に\(z\)で高さを表します。
\(\boldsymbol{\nabla} ^2\)の極座標変換
さて座標の話はここまでで、ここからは演算子の座標変換について考えてみたいと思います。
シュレディンガー方程式には\(\boldsymbol{\nabla} ^2\)が出てきます。
ネタバレをしてしまうと、水素原子の電子について計算する場合は極座標で計算するのが普通ですので、今回はその前準備として、極座標での\(\boldsymbol{\nabla} ^2\)の導出を行っていきます。
計算上の注意点
今回示す最終的な結果に至る過程で、こんな風に偏微分の順番は入れ替わっても、値は変わらないという前提の操作を行います。
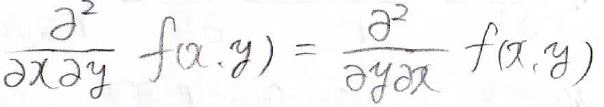
ですが、これは数学的には常に成り立つものではなくて、偏微分する関数が\(C^2\)級である必要があります。
\(C^2\)級というのは、2回偏微分することが可能で、さらに4つすべての2階偏導関数が連続であるという事を言います。
そのため、本来この操作を行うためには、この関数が\(C^2\)級であることを確かめないといけない(シュワルツの定理)ですが、サイエンスをやっている人がこの確かめをすることはほとんどありません。
それは、サイエンスの分野で扱う実用的な関数では偏微分の順序交換が成り立つことがほとんどだからです。
僕らは当たり前のように順序交換をしますが、数学的にそれはタブーだということは覚えておいてください。
実際に変形してみた
\(x\)、\(y\)、\(z\)を極座標で、また逆に\(r\)、\(\theta\)、\(\varphi\)を直交座標で表すとこんな感じになります。
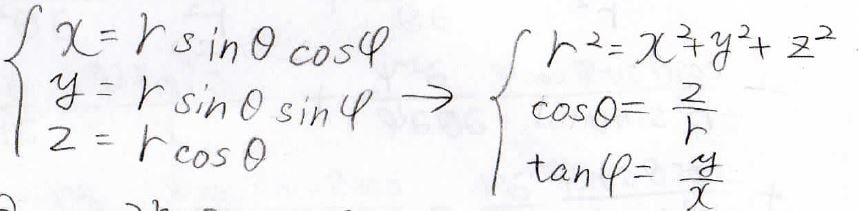
\(\frac{\partial }{\partial x}\)は\(r\)、\(\theta\)、\(\varphi\)を使ってこんな形になるので、波線を引いた部分を\(x\)、\(y\)、\(z\)が入らない形にしてあげれば完全に極座標に変換できます。
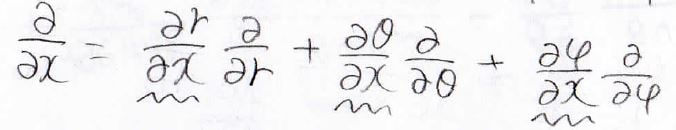
では始めに\(\frac{\partial r}{\partial x}\)を考えてみると、\(r^2=x^2+y^2+z^2\)より、こんな式が得られます。
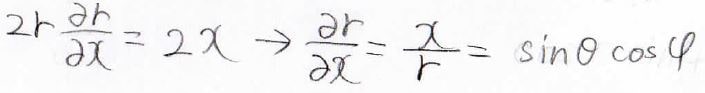
そこから、\(\frac{\partial r}{\partial x}\)は\(\frac{x}{r}\)という事になり、これを極座標で表すと\(\sin \theta \cos \varphi\)となります。
同じようにやっていくとこんな風になります。

これを\(y\)と\(z\)についてもやった結果、こうなります。
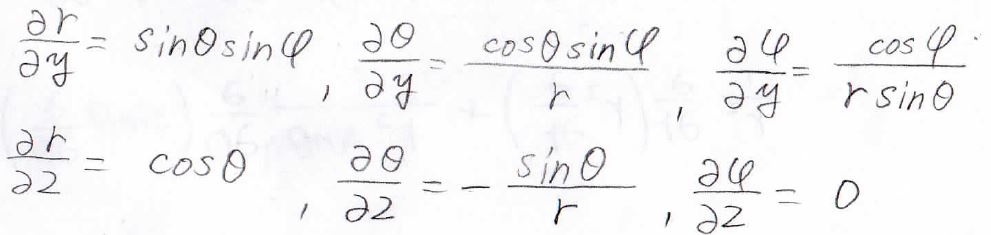
この結果より、\(\frac{\partial }{\partial x}\)は次のようになりました。
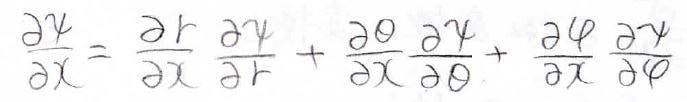
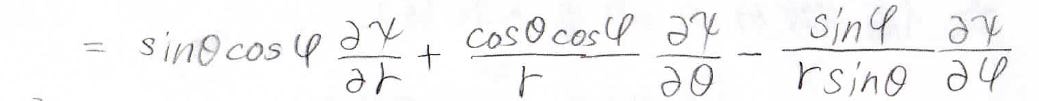
\(\frac{\partial ^2}{\partial x^2}\)の2階偏導関数を求める場合は、関数の積の微分の公式を使います。
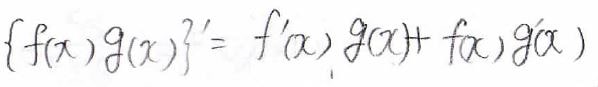
すると、こんな形になります。
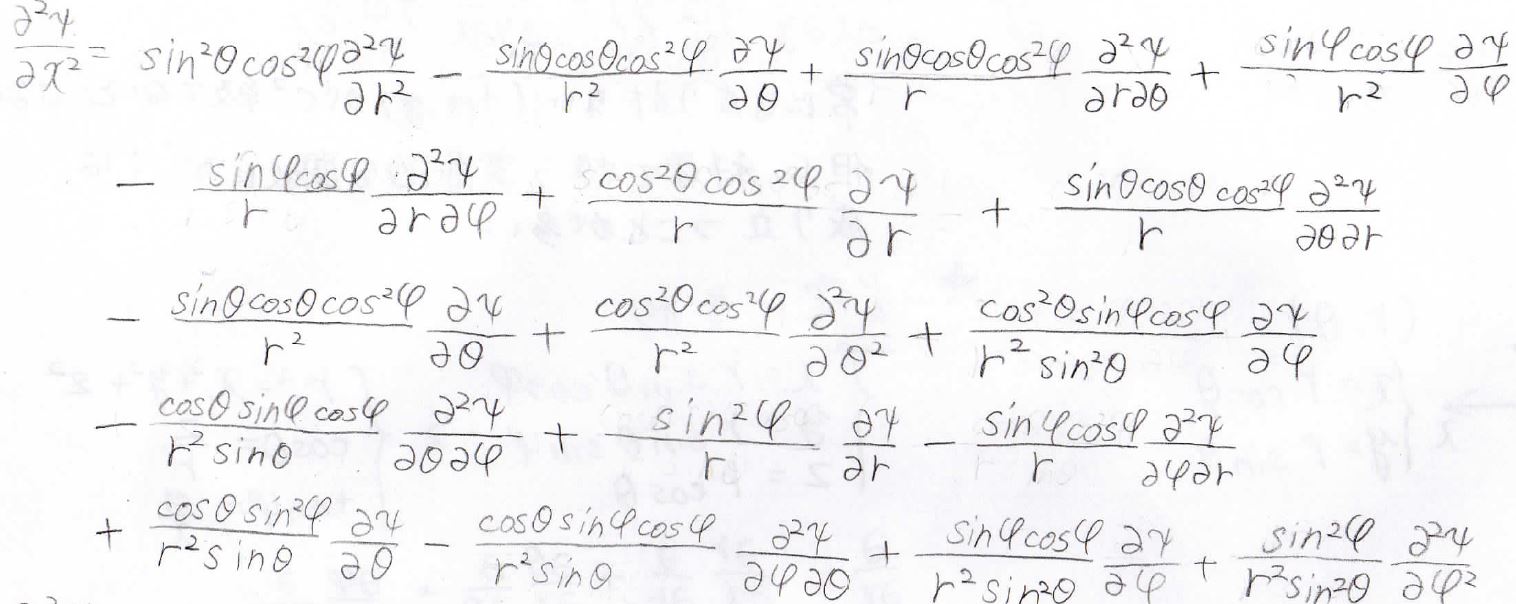
これを\(y\)、\(z\)についてもやってみると、以下のようになります。
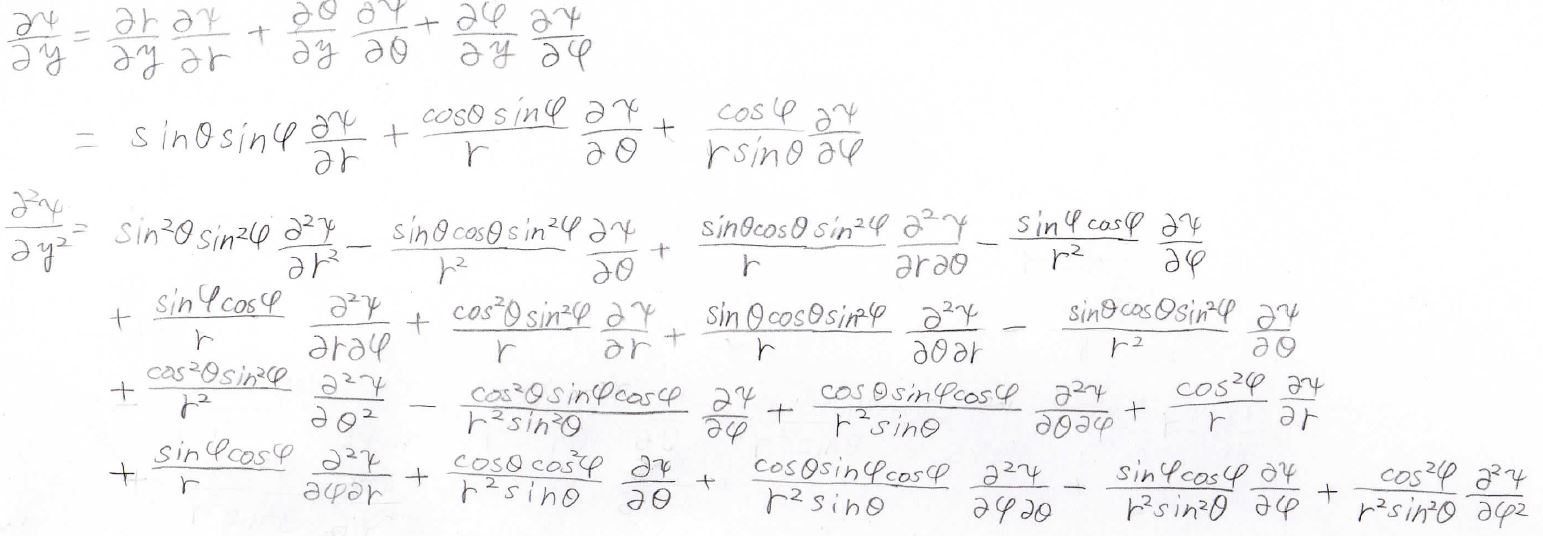
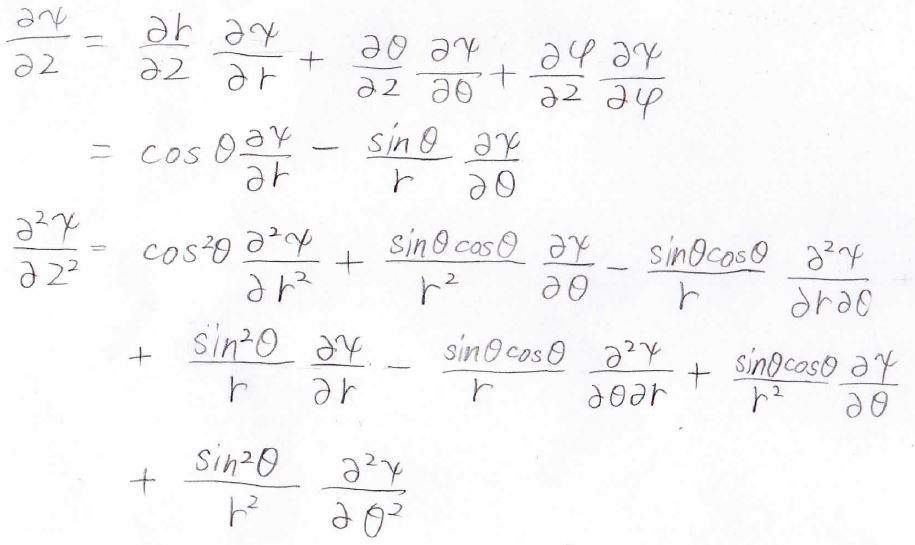
キャンセルする部分がいくつもあって、最終的に得られる\(\boldsymbol{\nabla} ^2\)は次の形になります。
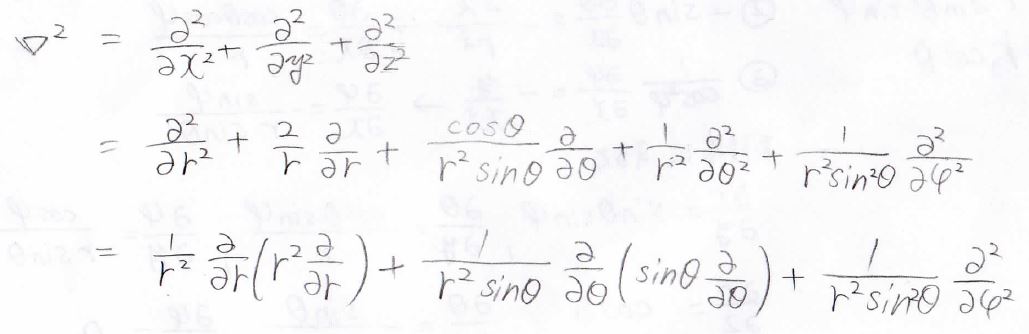
大変な変形なので、わざわざ自分でやってみる必要もないとは思いますが、やり方だけ知っておいてもらえたらと思います。
練習問題
では恒例の練習問題と行きましょう!
さっきは三次元でやったんですが、じゃあ二次元ならどうなる?ということで\(\frac{\partial ^2}{\partial x^2}+\frac{\partial ^2}{\partial x^2}\)を\(r\)と\(\theta\)を使って表してみてくださいという問題です。
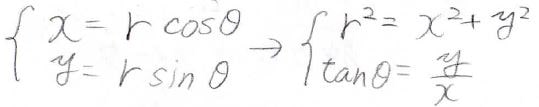
これならそこまで時間もとらないはずなので、ぜひやって頂ければと思います。

まず、\(\frac{\partial}{\partial x}\)と\(\frac{\partial}{\partial y}\)はこの形になります。
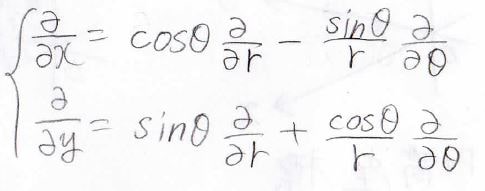
最終的に\(\frac{\partial ^2}{\partial x^2}+\frac{\partial ^2}{\partial x^2}\)はこのような形となります。
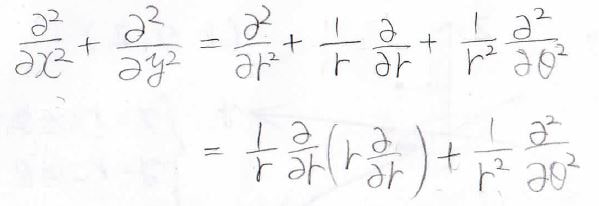
まとめ
はい、今回の内容は以上です。
おさらいをしておくと、まず次元というのは独立なパラメータの数を表し、同じ次元であれば変数変換が可能ということでした。
そして、今回は\(\boldsymbol{\nabla} ^2\)という演算子を極座標に変形するという話をしましたが、そこでは偏微分の順序交換を行っています。
この操作はサイエンスで扱う実用的な関数では成り立つことがほとんどなので、特に確かめることなく当たり前のようにやっていますが、数学的には常にできると限らないので、特に数学を専攻している人の前では注意しましょう。
変形の過程は大変なので、ここで再度書くことはしませんが、どんなやり方で変形が行われるのかということは重要なので、一回は理解していただければと思います。
最終的に得られた\(\boldsymbol{\nabla} ^2\)の極座標表示は別に覚える必要はないと思いますが、出てきたときに、何これ??とならないように今回紹介させていただきました。
それでは、どうもありがとうございました!