こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(second law)
それでは内容に入っていきます!
熱力学第二法則の身近な例
始めに、熱力学第二法則とは何か簡単に説明します。
例えば、閉じられた容器の中に温度\(T_1\)の物体と温度\(T_2\)の気体があったとします。
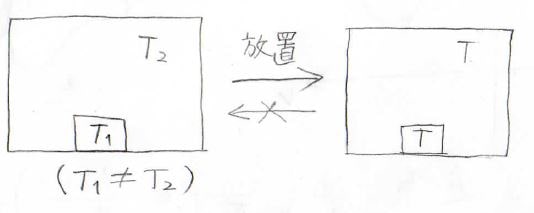
\(T_1\)と\(T_2\)が異なる温度だったときには、しばらく放置することで右のように、温度が均一になります。
これはごくごく当たり前の現象ですね。
ただここで重要なのは、一度均一な温度となったあとに、何も手を加えることなく再び不均一にはならないということです。
一度冷めてしまった料理も、電子レンジなどで外からエネルギーを与えない限り温かくはなりません。
熱の例以外でも同じことが言えて、例えば、ボールを高いところから落とすと、地面に何度かバウンドしたあと、静止します。
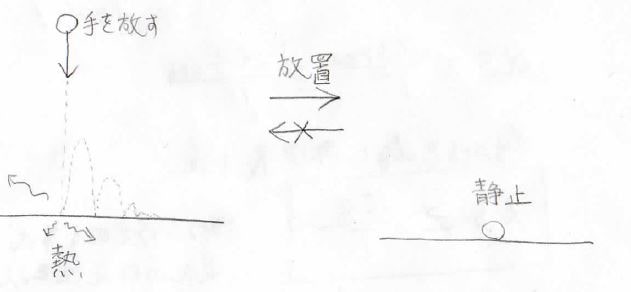
運動エネルギーの一部が地面、そして周りの気体分子に奪われ熱として広がっていくため、このようになります。
そして、一度静止したボールが周りからエネルギーを勝手に集めて、再び上に跳ね上がるということは起こりません。
以上のように自発的な変化の方向というのは、秩序立ったものから無秩序へ、あるいは不均一から均一へ広がっていくようになっています。
これが熱力学第二法則です。
そして、この散逸の度合いを新たな状態量として定義することで、変化の自発性を式として表現できるようになります。
この物理量をエントロピーといい、\(S\)と表します。
熱力学第二法則の表現
そして、熱力学第二法則には、いろいろな表現方法が存在しています。
すべて同値なのですが、ここではケルビンの法則、クラウジウスの法則というものを紹介します。
ケルビンの法則(トムソンの原理)
まず、ケルビンの法則は、熱源から熱を吸収して、そのすべてを仕事に変換することはできないというものです。

つまり、熱機関は低温熱源へ熱を捨てないといけないということです。
クラウジウスの法則(クラウジウスの原理)
そして、クラウジウスの法則は、低温熱源から高温熱源へ自発的に熱が流れることはないというものです。
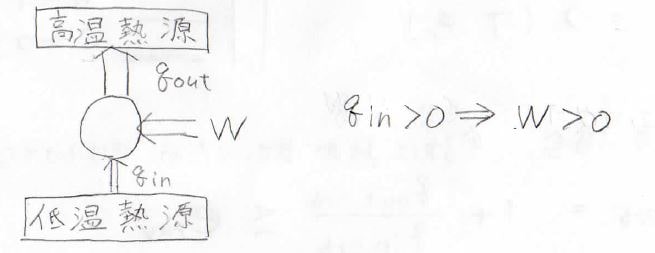
これは、冒頭でもお話したとおり、均一な温度になる方向にしか熱は流れないということを言っています。
このため、低温熱源からさらに熱を奪うためには逆カルノーサイクルなどにより、外部から仕事をする必要があります。
カルノーサイクルとエントロピー変化
それでは、カルノーサイクルを例にエントロピーを考えていきます。
過去の記事でカルノーサイクルの仕事や熱についてまとめていますが、実はその記事で説明した熱機関を作ることはできません。
カルノーサイクルの記事は、こちらです。

あくまで理想の話で、本当はタービンが回ったときの摩擦や容器の熱容量が有限であることなどの影響を考えないといけません。
この摩擦の影響がない循環機関は、可逆系と呼びます。
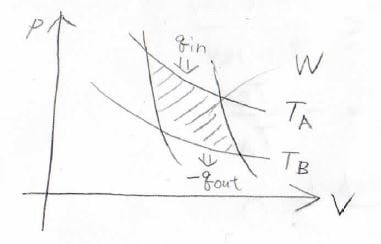
このときには、等温膨張で受け取った熱量\(q_\rm{in}\)が等温収縮で外部へ放出した熱量\(-q_\rm{out}\)と外部へした仕事\(W\)との和で書けます。

また、高温熱源の温度を\(T_\rm{A}\)、低温熱源の温度を\(T_\rm{B}\)とすると、熱効率は\(\displaystyle 1-\frac{T_\rm{B}}{T_\rm{A}}\)とも書けます。
これを整理すると、\(\displaystyle \frac{q_\rm{out}}{q_\rm{in}}=-\frac{T_\rm{B}}{T_\rm{A}}\)となります。

さらに変形すると\(\displaystyle \frac{q_\rm{in}}{T_\rm{A}}+\frac{q_\rm{out}}{T_\rm{B}}=0\)となり、これが可逆系で成り立つ式となります。
ここで、新しい状態量のエントロピー\(S\)を定義します。

その定義は、微小変化量\(\rm{d}\)\(S\)が可逆系へ与えられた微小な熱量\(\rm{d’}\)\(q_\rm{rev}\)を絶対温度\(T\)で割ったものになるというものです。
revはreversibleの意味で、単位は\(\rm{J}\)\(\ /\ \rm{K}\)などになります。
変化全体のエントロピー変化\(\Delta S\)は、この微小量\(\rm{d}\)\(S\)を可逆変化の経路に沿って積分した値になります。
補足(熱力学第三法則)
ここで、変化の自発性の議論に必要になるのは、あくまでエントロピーの変化量であって絶対値ではありません。
少し先の話をすると、一部の例外を除いて\(0\ \rm{K}\)でのエントロピーは\(0\)になります。
これを熱力学第三法則と言います。
そのため、エントロピーの絶対値は決められないというわけではありません。
また、統計力学により、こちらのボルツマンの式が導かれています。

\(k_\rm{B}\)はボルツマン定数、\(W\)はとりうる微視的状態の数、つまり高校数学で習った場合の数です。
ボルツマン分布の式より、一部例外を除き、絶対零度付近ではすべての分子が基底状態にあるため、場合の数は\(1\)になり、その対数をとってエントロピーは\(0\)になると予想できます。
温度が高いときには、分子はいろいろなエネルギー状態をとれるようになるため、どの分子がどの状態にあるのかという場合の数が大きくなります。
すると、エントロピーも大きくなります。
このように、バラバラに分布するほどエントロピーは大きくなるので、エントロピーは煩雑さを表す状態量であると説明されます。
ボルツマンの式導出、熱力学第三法則については、こちらを参照してください。


(補足おわり)
それではもう一度、カルノーサイクルの話に戻りましょう。
カルノーサイクル1周分のエントロピー変化\(\Delta S\)は、\(p\)-\(V\)グラフ上の可逆変化の経路に沿って、微小エントロピー変化を積分したものです。
断熱過程では熱の出入りがないため、エントロピー変化はありません。
そして、等温過程では\(\displaystyle \frac{1}{T}\)が積分の外に出せるので、\(\displaystyle \Delta S=\frac{q_\rm{in}}{T_\rm{A}}+\frac{q_\rm{out}}{T_\rm{B}}\)となります。
これは先ほども言ったとおり、\(0\)になります。
したがって、摩擦などがない可逆系では、エントロピーは一定となります。
そして、不可逆系では摩擦などにより熱が多く逃げるため、系が外部へする仕事は少なくなります。
つまり、熱効率が可逆系のときに比べて小さくなります。
いま、任意の系の熱効率を\(e_\rm{arb}\)とすると、その最大値は可逆系の熱効率\(\displaystyle 1-\frac{T_\rm{B}}{T_\rm{A}}\)になります。

arbはarbitraryの略です。
等温過程でのみ熱の出入りがあったとすると、\(\displaystyle \frac{q_\rm{in, arb}}{T_\rm{A}}+\frac{q_\rm{out,arb}}{T_\rm{B}}\)は\(0\)以下ということになります。
より一般的には、微分量を使って、下のように書けます。

これをクラウジウスの不等式と言います。
それで、このような任意の熱機関でも細分化すれば、カルノーサイクルの足し合わせで表現できます。
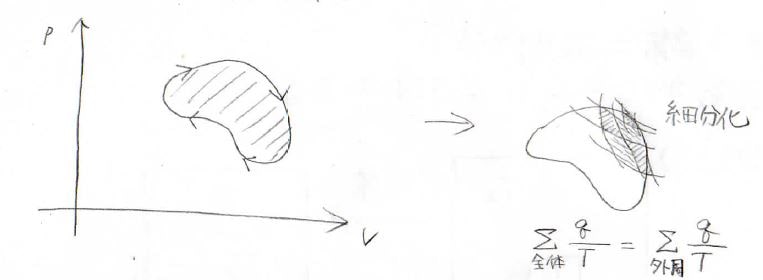
このサイクルの内側での熱のやり取りはキャンセルされるので、すべて足したものは外周だけ考えたものと同じになります。
よって、\(\displaystyle \frac{q}{T}\)の和と可逆性の関係も同じです。
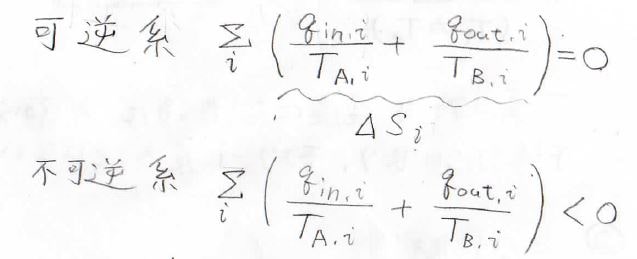
そして、この\(\displaystyle \frac{q}{T}\)の値は可逆系で\(0\)、不可逆系で\(0\)未満となることから、エントロピーの微小変化\(\rm{d}S\)は必ず任意の系に与えられた微小な熱量\(\rm{d’}\)\(q\)を\(T\)で割った値以上になります。
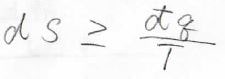
教科書によっては、こちらをクラウジウスの不等式というものもあります。
さらに、外界との熱のやり取りがない孤立系では、\(\rm{d’}\)\(q=0\)であるため、エントロピー変化\(\rm{d}\)\(S\)は\(0\)以上となります。
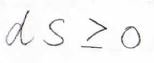
つまり、孤立系ではエントロピーが減少するような変化は自発的に起こり得ないということになります。
これをエントロピー増大則といって、これから何回も出てくる重要な式になります。
ちなみに、100年よりも前は、このエントロピー増大則を理由に、分子数が1万を超える高分子は存在できないという考えが主流でした。
なぜエントロピー増大則が根拠になったのか、そして、いかにして高分子の存在が認められたのか、こちらの記事で説明しています。
練習問題
それでは最後、練習問題をやってみましょう。
今回紹介した式を使って、前半で紹介した熱力学第二法則の2つの表現を証明してみましょう。
エントロピー増大則を使う場合は、外界との熱のやり取りがない孤立系でのみ成り立つ法則なので、いかにして孤立系を見つけるかがポイントになります。
まず、ケルビンの法則については、受け取った熱をすべて仕事に変換できる熱機関が存在すると仮定します。
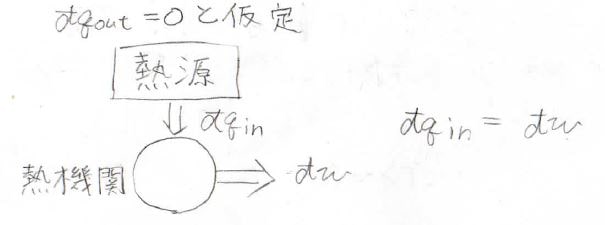
熱機関1サイクルについて、\(\displaystyle \frac{\rm{d’}\mathit{q}}{T}\)を積分すると、\(\displaystyle \frac{q_\rm{in}}{T}\)となり、この値は必ず正になります。

これは、クラウジウスの不等式に反するため、このような熱機関は存在しないという結論に至ります。
そして、クラウジウスの法則についても、まずは低温熱源から高温熱源への熱の移動が自発的に起こったとします。
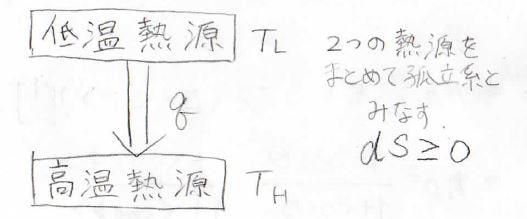
このとき、2つの熱源をまとめて孤立系とみなすと、\(\rm{d}\)\(S=\displaystyle -\frac{\rm{d’}\mathit{q}}{T_\rm{H}}+\frac{\rm{d’}\mathit{q}}{T_\rm{L}}\)となります。

ここで\(T_\rm{H}\)は高温熱源の温度、\(T_\rm{L}\)は低温熱源の温度です。
\(T_\rm{H}\)は必ず\(T_\rm{L}\)より高い温度であるため、その逆数同士の関係は反対になります。
すると、\(\rm{d}\)\(S\)は必ず負の値をとることになります。
これはエントロピー増大則に反するため、そもそもこのような熱の移動は自発的に起こりません。
以上のように、周りの大気もまとめて孤立系とみなす考え方は、これから何回も出てきますので、ぜひここで慣れておいてください。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




