こんにちは!
それでは今回も数学の続きやっていきます。
今日のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(determinant definition)
行列式の定義
まず、行列式の定義の話をします。
行列式は正方行列に対して定義できるものでして、英語ではdeterminantと言います。
それのdetを取って\(\det{\bf{\rm{A}}}\)や\(|\bf{\rm{A}}|\)のような表し方がされます。
この行列式が何を意味するのかは、こちらの記事にまとめてありますので、この記事を読み終わってから、読んでみてください。

今回は、とりあえず行列式というものを考えるんだということだけ思いながら見ていただければと思います。
まず、行列式の定義はこのような式です。
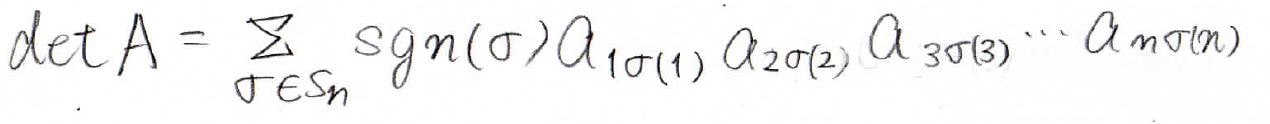
ここで、\(\sigma\)は置換のことで、\(\rm{sgn}\)は符号関数です。
どちらも以前の記事で解説していますので、こちらを合わせてご覧ください。


それで、\(S_n\)というのは\(n\)次のすべての置換の集合で、\(n!\)個分の置換が含まれています。
2次行列式の解法
そして、例えば\(2\)次正方行列の行列式は、このような式になります。
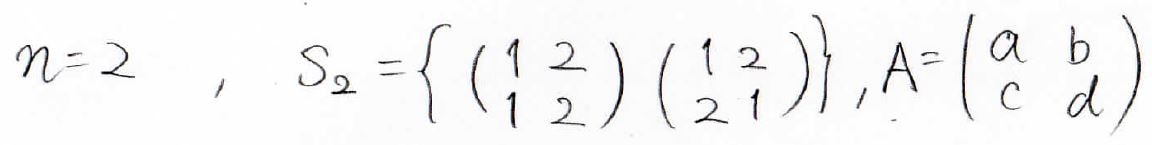
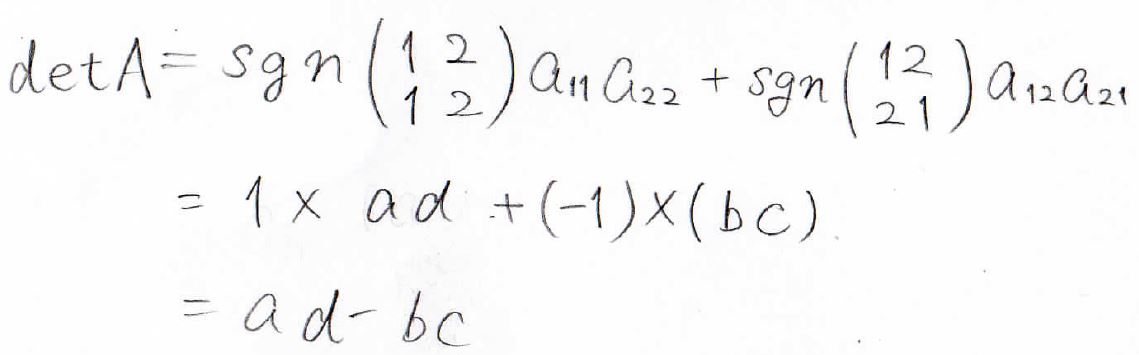
行列の各成分を\(a\)、\(b\)、\(c\)、\(d\)で表したとき、\(2\)次行列式の値は\(ad-bc\)で与えられることになります。
模式的に書くと下図のように、左上から右下にかけての値の積はプラスで、反対側の対角線上の成分の積はマイナスになります。

\(2\)次の行列式を実際に計算してみると、こんな感じです。
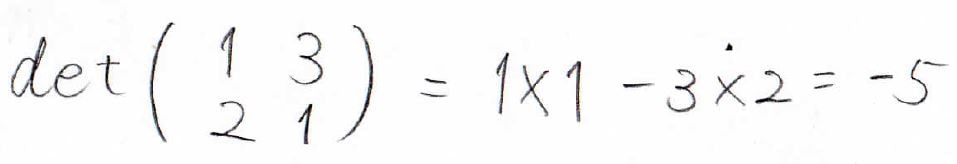
3次行列式の解法
そして\(3\)次行列式の場合も比較的簡単に解くことができます。
次数が\(3\)の置換は全部で6つの項が出てきて、符号関数によって正と負の項がそれぞれ3個ずつになります。
そこで、まずは正になる部分だけを考えます。

すると定義より、この3本の曲線上のそれぞれ3つの値の積が1つの項になります。
負について見るときは、今度こちらの青線上の値の積を1つの項とみなします。
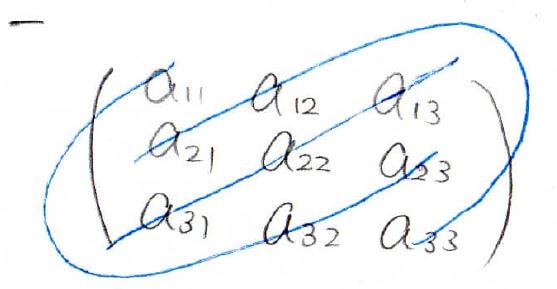
この方法はサラスの方法と呼ばれます。
例えば、以下のように3次の行列式は求めます。
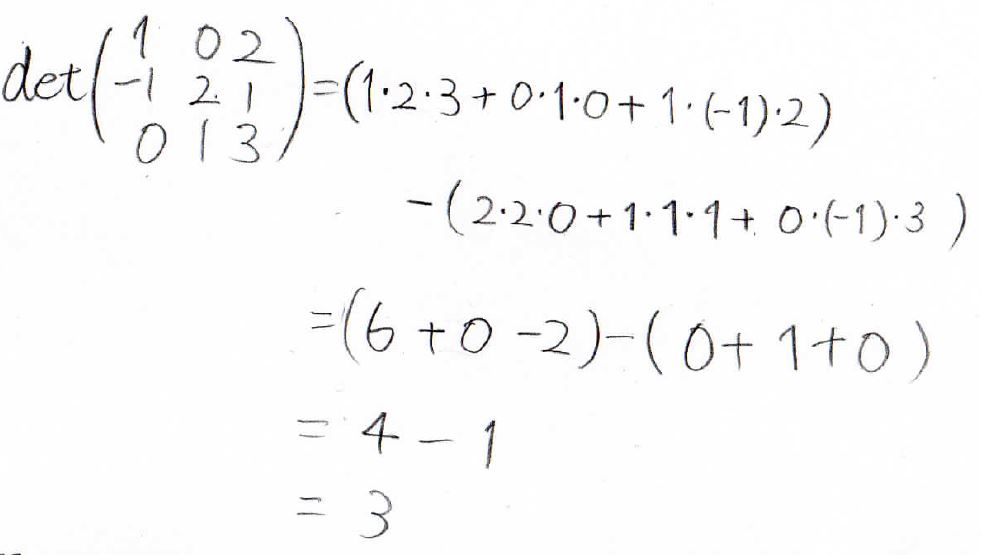
練習問題
はい、それでは恒例の練習問題です。
これら2つの行列式を求めてみてください。
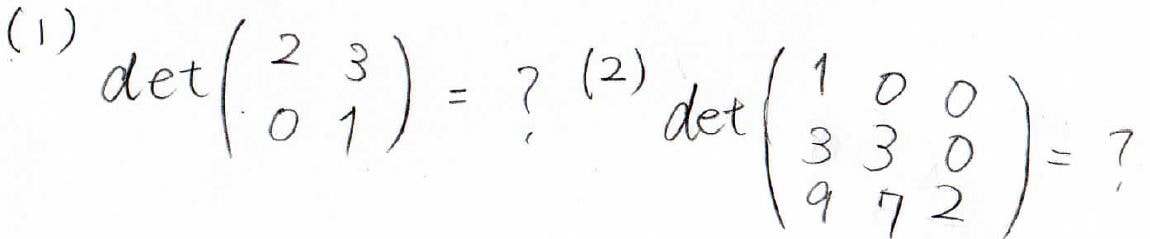
(1)では斜め同士の引き算をして、\(2-0\)で\(2\)が答えになります。
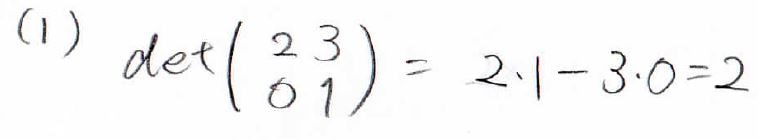
そして(2)ではサラスの方法よりこう書けるのですが、6つの項のうち5つに\(0\)がかかっているので結局、対角成分の積である\(6\)となります。
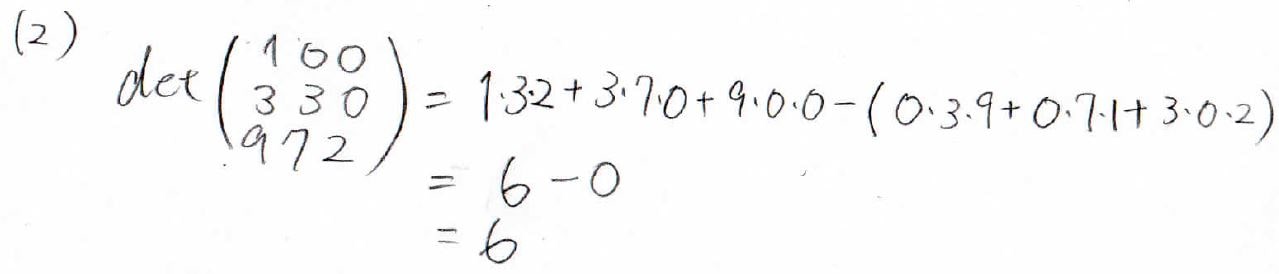
このように、上三角・下三角行列の行列式は対角成分の積で与えられます。
詳しい話は次の記事でお話ししていきます。

まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




