こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(steady-state approximation)
それでは内容に入っていきます!
定常状態とは
まず、定常状態という言葉の意味について、少しお話しします。
化学に限らず、自然科学の広い分野で使われる言葉ですが、時間に対して一定で、変化がない状態というのがもともとの意味です。
熱力学や統計力学の分野では、平衡状態との区別は次のようになされています。
熱力学的平衡状態とは、巨視的な量が一定となっている状態のことを言います。
一方、巨視的な量の時間変化はあるが、その速度が一定である状態のことを非平衡定常状態、もしくは定常状態と言います。
定常状態近似
ここで、前回お話しした逐次素反応の系について、反応速度論において用いられる定常状態近似を説明します。
考える化学反応は、反応物\(\rm{A}\)が中間体\(\rm{I}\)に変化し、さらに生成物が\(\rm{P}\)に変化するというものです。
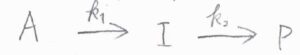
逆反応は起こらず、2つの素反応はともに\(1\)次素反応であるとします。
反応速度定数は、それぞれ\(k_1\)、\(k_2\)とします。
反応開始前は、\(\rm{A}\)しか存在していないものとします。
そのとき、\(\rm{A}\)、\(\rm{I}\)、\(\rm{P}\)のモル濃度の時間変化は、こちらの式で与えられます。
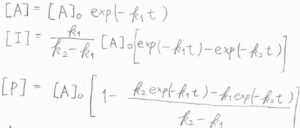
\(t\)が時刻で、\([\rm{A}\)\(]_0\)が時刻\(0\)における\(\rm{A}\)のモル濃度です。
導出過程は、こちらを参照してください。

横軸に\(t\)、縦軸にそれぞれのモル濃度をとると、次のようになります。
まず、こちらのグラフは、1段階目の反応の方が2段階目よりも速い場合です。
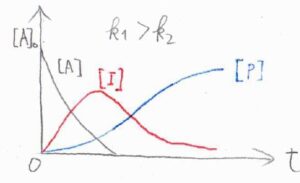
中間体でいる時間が長く、モル濃度の最大値も大きくなります。
対して、こちらのグラフは、2段階目のほうが速い場合です。
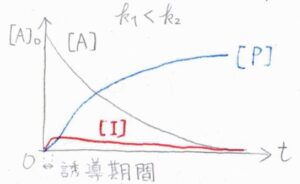
生成した中間体は、ただちに\(\rm{P}\)へと変化するため、中間体でいる時間は短く、モル濃度の最大値は小さくなります。
反応開始直後の中間体濃度が増大する期間のことは、誘導期間と言われます。
先ほどの式は、近似を使わずに微分方程式を解くことでモル濃度を求めた結果ですが、\(\rm{P}\)の生成速度が\(\rm{A}\)の濃度にどのように依存するのかが複雑でわかりにくく、反応次数を決められません。
そこで、定常状態近似が出てきます。
反応速度論における定常状態とは、中間体の生成速度と分解速度が等しい状態のことを言います。
先ほどの2つめのグラフでは、誘導期間よりも時間が経過した後であれば、中間体の濃度は十分低く、その時間変化を無視できるとしても大きな問題はないと考えられるので、\(\displaystyle \frac{\rm{d}[\rm{I}]}{\rm{d}\mathit{t}}\approx 0\)と近似します。

これが定常状態近似です。
反応物、生成物のモル濃度の変化速度は\(0\)としないため、準定常状態近似、略してQSSAと表記されることもあります。
先ほどの逐次素反応で、定常状態近似を使うと次のようになります。
まず、\(\rm{I}\)についての速度式を考えると、\(\displaystyle \frac{\rm{d}[\rm{I}]}{\rm{d}\mathit{t}}=k_1[\rm{A}\)\(]-k_2[\rm{I}]\)であり、これが\(0\)になります。
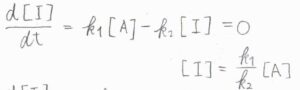
整理すると、\([\rm{I}\)\(\displaystyle ]=\frac{k_1}{k_2}[\rm{A}]\)となります。
これを再び時間について微分すると、\(\displaystyle \frac{\rm{d}[\rm{I}]}{\rm{d}\mathit{t}}=\frac{k_1}{k_2}\frac{\rm{d}[\rm{A}]}{\rm{d}\mathit{t}}\)となります。
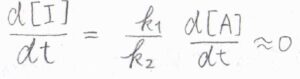
これが\(0\)と近似でき、かつ\(\displaystyle \frac{\rm{d}[\rm{A}]}{\rm{d}\mathit{t}}\)は\(0\)ではないため、定常状態近似が使える条件は、\(k_1\ll k_2\)、すなわち1段階目の素反応に比べて、2段階目の素反応のほうがとても速いときということになります。
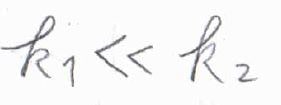
このとき、\(\rm{P}\)の生成速度\(\displaystyle \frac{\rm{d}[\rm{P}]}{\rm{d}\mathit{t}}=k_2[\rm{I}]\)に、\([\rm{I}\)\(\displaystyle ]=\frac{k_1}{k_2}[\rm{A}]\)を代入すると、\(\displaystyle \frac{\rm{d}[\rm{I}]}{\rm{d}\mathit{t}}=k_1[\rm{A}]\)となります。
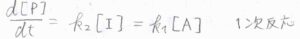
したがって、全体の反応は\(1\)次反応であると言えます。
近似を使うことで、簡単に反応次数を求めることができました。
もう1つ注目したいのは、2段階目の反応速度定数\(k_2\)はどこにも残っておらず、1段階目の反応速度と全体の反応速度が等しいという結果になっていることです。
全体の反応速度を決める素反応のことは律速段階、略称RDSと言います。
\(\rm{d}\)\([\rm{P}]\)を時刻\(0\)から\(t\)まで定積分すると、\(\rm{P}\)のモル濃度がわかります。
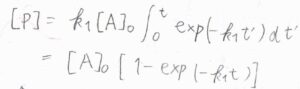
計算すると、\([\rm{P}\)\(]=[\rm{A}\)\(]_0[1-\exp{(-k_1t)}]\)となります。
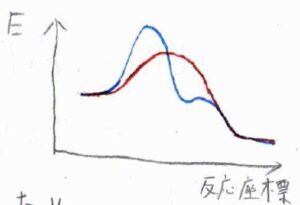
グラフにすると、下図のようになります。
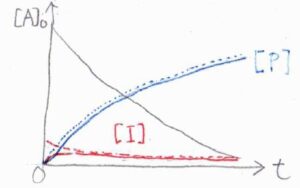
点線が定常状態近似を使った結果、実線が近似を使わなかった結果です。
反応開始直後の誘導期間では、両者にある程度の差が生じますが、長時間側で両者の結果はかなり近い値となります。
律速段階
最後、先ほど出てきた律速段階について補足します。
アレニウスの式より、一般的に反応速度定数が大きいということは、活性化エネルギーが小さいということを意味します。
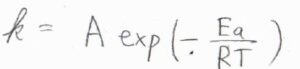
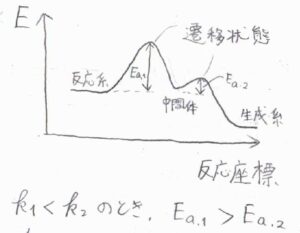
※頻度因子\(A\)の違いが無視できない場合や、そもそもすべての変化がアレニウス型ではないということを考慮して、ここでは「一般的に」と付けています。
多くの場合、活性化エネルギーが最も大きい段階が律速段階となり、その素反応の次数によって、全体の反応次数も決まります。
先ほどのように、最初の素反応が律速である場合は、その反応速度がそのまま全体の反応速度になります。
最も活性化エネルギーが大きい素反応が律速段階とならない例
ただし、最も活性化エネルギーが大きい段階が常に律速段階となるわけではありません。
ここでは例外となる例を2つ紹介します。
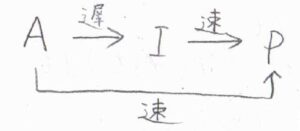
別の速い反応経路がある場合
まず、別の反応経路があり、そちらのほうが速く進行する場合は、遅い経路はほとんど経由しないため、律速段階とは言えず、反応次数にも影響しません。
反応物の濃度がきわめて低い場合
また、反応物の濃度がきわめて低いときには、活性化エネルギーの小さい素反応のほうが遅くなることがあります。
例えば、反応物\(\rm{A}\)と\(\rm{B}\)があって、1段階目では\(\rm{B}\)は関与せず、\(\rm{A}\)だけが中間体\(\rm{A’}\)へ変化するとします。

そして、\(\rm{A’}\)と\(\rm{B}\)が反応して生成物\(\rm{P}\)になる反応があったとします。
このとき、1段階目の活性化エネルギーのほうが大きく、反応速度定数が小さかったとしても、\(\rm{B}\)の濃度がきわめて低いときには2段階目のほうが遅い反応になることがあります。
そのような場合は2段階目が律速となるため、活性化エネルギーの大小関係では、律速段階を見誤ることがあります。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!