こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(third law)
ボルツマンの式
まず、2つ前の記事で導出したボルツマンの式についておさらいをします。

統計力学によって\(\rm{d}\)\(S=k_\rm{B}d\)\((\ln{W})\)という式が導かれます。
ここで、\(S\)はエントロピー、\(k_\rm{B}\)はボルツマン定数、\(W\)はとりうる微視的状態の数です。
この式を\(0\ \rm{K}\)から温度\(T\)まで積分すると、\(S=k_\rm{B}\)\(\ln{[W(T)]}-k_\rm{B}\)\(\ln{[W(0)]}\)となります。
今回は、\(0\ \rm{K}\)におけるエントロピーである\(\displaystyle -k_\rm{B}\)\(\ln{[W(0)]}\)について考えていきます。
ネルンストの熱定理
ここからが新しい内容です。
まず、絶対零度まで物質を冷却していくことを考えましょう。
温度が高いうちは、氷やドライアイス、液体窒素などの冷媒を使うことができますが、いずれも\(0\ \rm{K}\)までは冷却できません。
物体の温度を\(T_\rm{A}\)、冷媒の温度を\(T_\rm{B}\)として、均一な温度\(T\)に達するまで放置したとすると、\(T\)は必ず\(T_\rm{B}\)より高く\(T_\rm{A}\)より低い温度になるはずです。

したがって、\(0\ \rm{K}\)まで冷却したいときには、絶対温度がマイナスとなる冷媒が必要となります。
そのようなものは存在しないため、\(0\ \rm{K}\)まで冷却することはできません。
そして、次に\(\rm{A}\)という物質が2つの\(\rm{B}\)という物質に分解するという化学反応について、エントロピーの変化を考えて見ましょう。
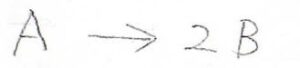
ここでは簡単のため、各状態のエネルギー間隔は\(\rm{A}\)と\(\rm{B}\)で変わらないとしておきます。
まず、十分に高い温度で、この反応が起こった場合、分子数の分布はこのようになります。
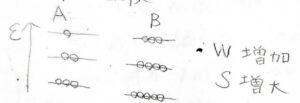
分子数が増えたことで、微視的状態の数\(W\)が大きく増加します。
したがって、エントロピーも増大することになります。
一方、\(0\ \rm{K}\)近傍では分子数が増えたところで、ほとんどの分子が基底状態にあるため、エントロピー増大の幅はとても小さいことになります。

つまり、エントロピー変化\(\Delta S\)は、温度を\(0\ \rm{K}\)に近づけていくと、\(0\)に収束すると予想されます。

ネルンストが実験的に確かめたことから、これはネルンストの熱定理と呼ばれています。
この定理は、すべての物質が秩序化している場合、いかなる物理的、化学的変化に伴うエントロピー変化も、温度を絶対零度に近づけていったときに\(0\)に近づいていくというものです。
先ほど挙げた分解のような化学的変化に限らず、例えば蒸発や融解、溶解などといった物理的な変化も含まれます。
そして、「秩序化している場合」とありますが、秩序化していないものとしては、分子がきれいに配列していない気体や液体、ガラス状態が挙げられます。
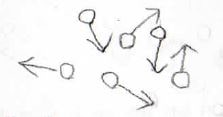
また、不純物や欠損を含む結晶も秩序化しているとは言えません。

熱力学第三法則
秩序だっている場合とは、下図のように、格子欠損や不純物が完全に取り除かれた結晶が該当します。

この結晶は、完全結晶と呼ばれます。
\(0\ \rm{K}\)にした極限が完全結晶となる場合、考えうる分子配列は\(1\)通り、微視的状態の数も\(1\)通りなので、その対数をとってエントロピーは\(0\)となります。
ネルンストの熱定理により、\(0\ \rm{K}\)における生成エントロピー\(0\)なので、これは物質の種類によらず、共通して言えることになります。
まとめると、完全結晶となるすべての物質のエントロピーは、絶対零度で\(0\)になるということになり、これを熱力学第三法則と言います。
ただし、実際には物体として結晶が存在する以上必ず表面があるため、そこが格子欠損となります。
また、結晶内部に格子欠損があったほうがむしろ熱力学的に安定になる場合がほとんどです。
つまり、完全結晶とはあくまで理想の状態であって、実際に作ることはできません。
残余エントロピー
最後に、\(0\ \rm{K}\)でもエントロピーが\(0\)にならない例があるので、紹介しておきます。
まずは、並び方の違いによるエネルギー差がほとんどない場合です。
例えば、\(\rm{AB}\)という異核二原子分子が結晶を作るときに、\(\rm{A}\)と\(\rm{B}\)が交互に現れる①のパターンと\(\rm{B}\)同士が隣接してしまった②のパターンができるとしましょう。
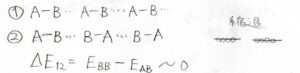
これらが同程度に安定である場合には、\(0\ \rm{K}\)で分子配列が1つに定まらないので、エントロピーは\(0\)より大きい値となります。
基底状態が縮退しているような物質でも、同じです。
そして、共有結合と水素結合が共存しているような結晶でも、エントロピーは\(0\)になりません。
水を例にすると、1つの酸素原子から伸びる4本の結合のうち、2本が共有結合、2本が水素結合となります。
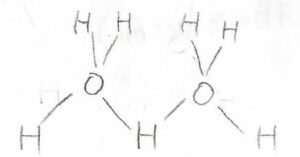
その選び方は、1つの酸素原子につき\(_4 C_2\)の\(6\)通りで、温度に依存しません。
したがって、エントロピーは\(0\)になりません。
実際に、\(0\ \rm{K}\)における水のモルエントロピーは\(3.4\ \rm{J K^{-1} mol^{-1}}\)と求められています。
絶対零度における\(\displaystyle 0\)ではないエントロピーは、残余エントロピーと呼ばれます。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




