こんにちは!
それでは今回も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(triatomic molecule)
三原子分子のとりうる構造
前回は等核二原子分子の話をしましたが、今回は三原子分子です。
前回の記事はこちらです。

三原子分子の形には、直線型と折れ線型の2パターンがあります。

これらの形は対称性が異なるため、軌道どうしの相互作用も変わってきます。
分子は、電子がもつエネルギーの総和が小さくなるほうの形をとることになります。
直線型分子
まず、直線型として代表的な二酸化炭素を例に、その対称性を考えていきましょう。
三原子分子の対称性を考えるときにまず必要なのは、中央の分子を無視した外側2つの原子の相互作用を考えることです。
二酸化炭素の場合は、炭素原子を無視して2つの酸素原子に着目します。

その相互作用は、結合距離が長くなった酸素分子をイメージしてください。
いま、2つの酸素原子の中心を結んだベクトルは、\(\displaystyle x\)軸に平行であるとして説明を続けます。
そして、次は炭素原子のみについて考えます。
\(\displaystyle \rm{s}\)軌道と\(\displaystyle \rm{p}\)軌道の対称性は、このようになります。
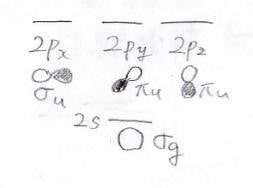
\(\displaystyle \sigma\)か\(\displaystyle \pi\)かは\(x\)軸方向から見たときに、波動関数の符号が入れ替わる節と言われる線が0本か1本かという違いです。
\(\displaystyle \rm{g}\)と\(\displaystyle \rm{u}\)は対称を意味するgerade(ゲラーデ)と反対称を意味するungerade(ウンゲラーデ)の頭文字で、炭素原子の中心から見て点対称か点反対称という違いです。
そして、先ほど考えた2つの酸素原子が作る軌道と炭素原子の軌道で同じ対称性をもつ者どうしが相互作用をすることで、もっと安定な状態ともっと不安定な状態を作ることができます。
例えば、\(\displaystyle \sigma_\rm{g}\)について考えると、下記のようになります。
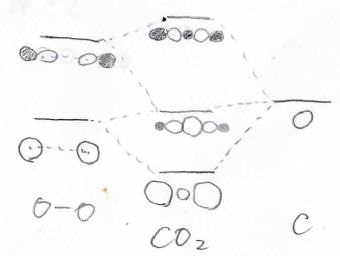
エネルギーが近い値になる軌道には大きく寄与が起こるので、一番下の分子軌道だと炭素原子の寄与が酸素原子たちの寄与より小さくなって、アンバランスな分子軌道になります。
\(\displaystyle \sigma_\rm{u}\)、\(\displaystyle \pi_\rm{u}\)については、下記のとおりです。
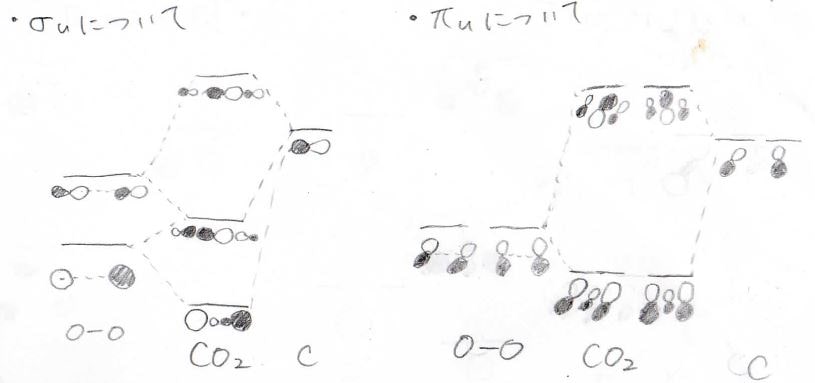
なお、\(\displaystyle π_\rm{g}\)は炭素原子の電子軌道にはない対称性であるため相互作用は起こらず、そのまま二酸化炭素の分子軌道になります。
折れ線型分子
対して、折れ線型ではどうなるのでしょうか。
ここでは、水分子について考えていきます。
折れ線型の対称性は、回転対称性と鏡映対称性で議論します。
回転対称
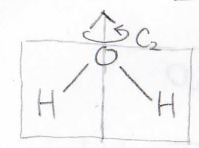
まずは上図で矢印を回転軸として\(180^\circ\)回すということを考えます。
すると、原子の位置は回転する前とぴったり重なるわけですが、このときに分子軌道の位相(符号)が合うものを\(\displaystyle a\)、逆位相(逆符号)になるものを\(\displaystyle b\)と表して区別することができます。
鏡映対称
三原子を結ぶ平面に対して面対称となっているものを\(\displaystyle 1\)、なっていないものを\(\displaystyle 2\)として区別できます。
水分子の分子軌道
それでは実際に、対称性を考えていきましょう。
まずは先ほどと同様に、両端の水素原子について考えます。

そして、中央の酸素原子の電子軌道はこのとおりです。
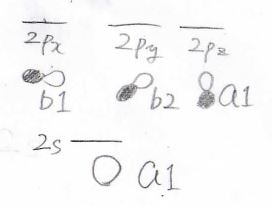
\(\displaystyle a_1\)どうし、\(\displaystyle b_1\)どうしで相互作用が起こります。
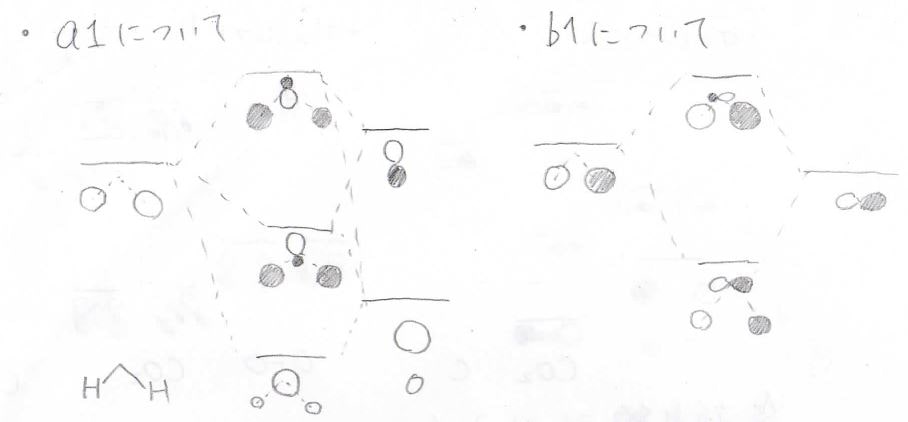
\(\displaystyle b_2\)は酸素原子にしかないため、そのまま水の分子軌道になります。
両者の比較
二酸化炭素と水の対称性を個別に考えてきましたが、両者の分子軌道はまとめると、こちらのようになります。

二酸化炭素では16個、水では8個の電子がこの分子軌道を占めることになり、基底状態では上記のような電子配置となります。
ここで、分子軌道を次の3つに分類することができます。
それは、分子になることで安定化が起こった結合性軌道、分子になることで不安定化が起こった反結合性軌道、そして、特に安定化も不安定化も起こらなかった非結合性軌道です。
二酸化炭素では\(\displaystyle \pi_\rm{g}\)、水では\(\displaystyle b_2\)が非結合性軌道にあたります。
二酸化炭素の\(\displaystyle \pi_\rm{g}\)は酸素原子2つ、水の\(\displaystyle b_2\)は中央の酸素原子1つだけで完結しており、三原子分子となった恩恵はありません。
ウォルシュ図
最後に、ウォルシュ図について紹介します。
これは、その分子がどのような結合角をとるのが安定なのかということを一般的に考えたものになります。
一言に折れ線型と言っても、その結合角は常に\(109.5^\circ\)ではないので、連続的に結合角を変化させたときにエネルギーがどのような変化を予想することができます。
何らかの原子\(\displaystyle \rm{A}\)を中心にした\(\displaystyle \rm{AH_2}\)という分子について、結合角を\(90^\circ\)にしたときの折れ線型、そして結合角が\(180^\circ\)の直線型の分子軌道は、このようになります。
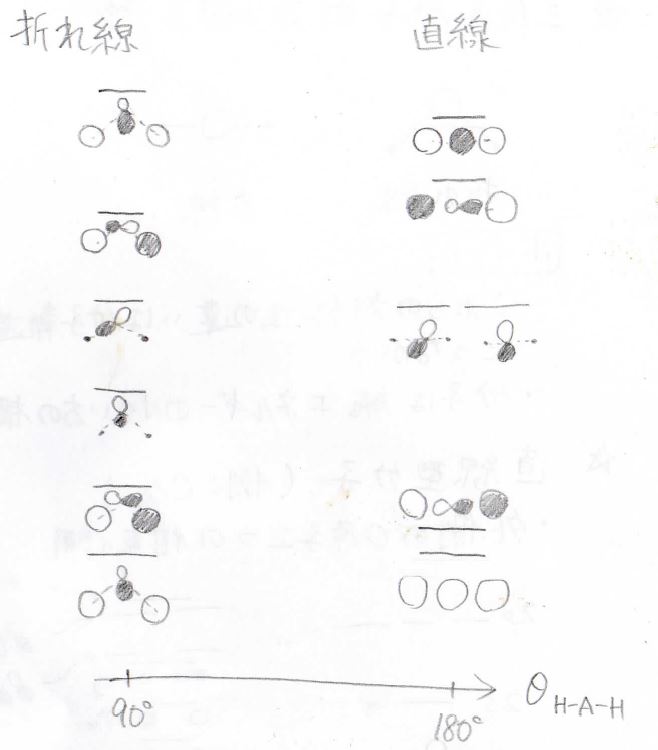
軌道によって複雑な大小関係になり、電子によって安定な構造が決まります。
そして、実際に計算した結果は電子が5個未満の場合には直線型、5個から8個ある場合には折れ線型であるという予想になります。

このことより、例えば、水素化ベリリウム\(\displaystyle \rm{BeH}_2\)は直線型、メチレン\(\displaystyle \rm{CH}_2\)は折れ線型と予想され、この予想は正しいです。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!