こんにちは!
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(wave equation)
古典的な波
波とは、同じパターンが繰り返し現れるもの、また、空間を通じて伝播するものです。
現実世界で波を記述する場合のパラメーターとしては振幅、周期、波長、位相のずれが挙げられます。
高校の物理で習ったように位置\(x\)と時刻\(t\)に依存する単一の波は、下の式で与えられます。
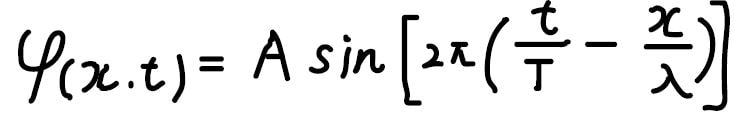
これに加えて周期や波長、振幅を変えた正弦波の和も、決まったパターンを示す波といえます。
波動方程式
今回は、より一般的に、波がどのような条件式を満たすのかという話をしていきます。
その前にまず、先ほどの関数について、\(\displaystyle \frac{2\pi}{T}\)を角周波数\(\displaystyle \omega\)、\(\displaystyle \frac{2\pi}{\lambda}\)を角波数\(\displaystyle k\)と書き換えておきます。
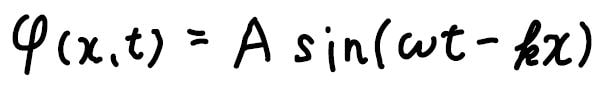
まず、偏微分を考えてみましょう。
偏微分とは、多変数関数をある変数以外固定した状態で微分する演算方法です。
例えば、\(t\)についての一階偏微分は、下のようになります。
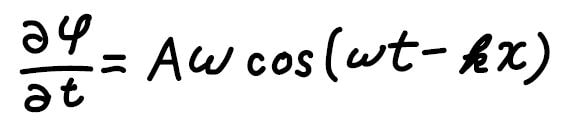
もう1つの変数である\(x\)は定数として、扱っています。
今度、これをもう一度\(t\)について微分してみましょう。
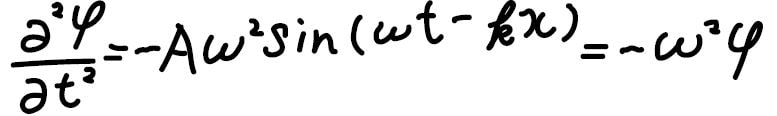
すると、\(A\sin^2{(\omega t-kx)}\)という元の波と同じものが現れるため、二階偏微分は\(-\omega ^2\varphi\)とも書くことができます。
同様に、\(x\)についても微分してみると、\(x\)の二階偏微分は\(-k^2\varphi\)になります。
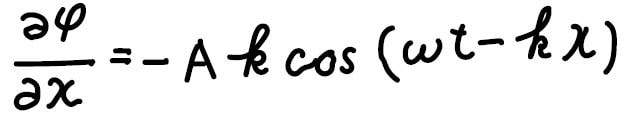
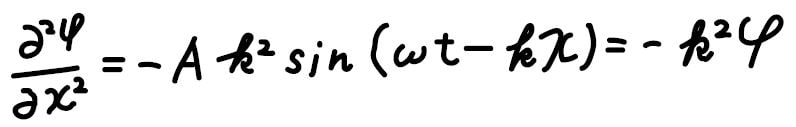
つまり、以下の関係が成り立ちます。
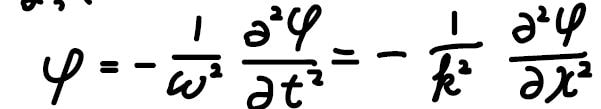
ここで、波長を周期で割ったものが波の速さに相当することから、\(\displaystyle \frac{\omega}{k}\)を速さ\(v\)と置くと、右のような等式が得られます。
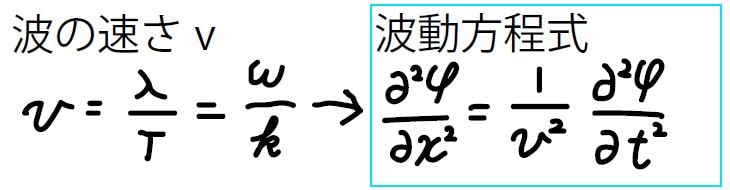
この式は、波であれば成り立つものであり、波動方程式と呼ばれます。
三次元空間での波動方程式
ここまで一次元で考えていたものを三次元に拡張すると、以下のようになります。
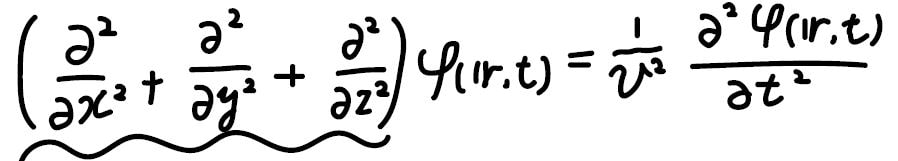
ここであるベクトル演算子を導入します。
\(\boldsymbol{\nabla}\)の記号はナブラと呼び、下のように定義されます。
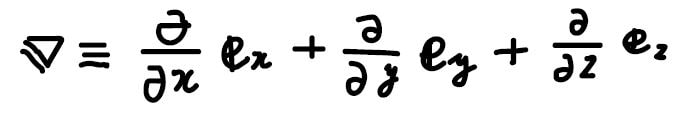
ここで、\(\boldsymbol{\rm{e}}\)は各軸方向への単位ベクトルを表しています。
左辺のかっこの中身は、\(\boldsymbol{\nabla}\)というベクトルどうしの内積\(\displaystyle \boldsymbol{\nabla}^2\)であり、これをラプラシアンと呼びます。
記号では、\(\Delta\)と表します。
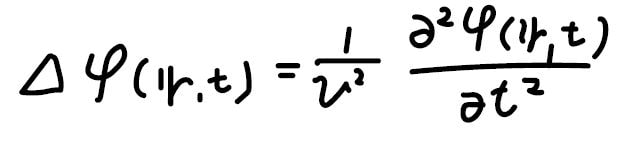
練習問題
最後、練習問題をやってみましょう。
高校物理で習った波は実数でしたが、実は、複素数でも波動方程式を満たすことがあります。
ということで、実際に\(\exp[\rm{i}(\mathit{\omega t-kx})]\)が波動方程式を満たすことを確かめてください。
このように、二階偏導関数が\(\sin\)と同じ結果になることから、\(\rm{e}\)の複素数乗は複素数の領域に拡張された世界での波であると言えます。
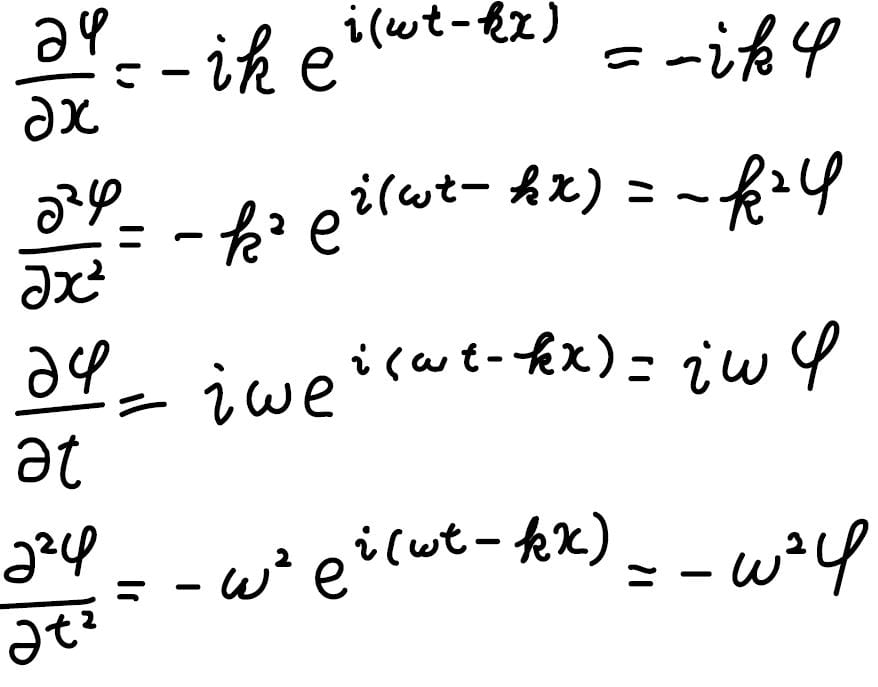
これは、量子力学をやるうえでとても重要なことなので、ぜひ覚えておいてください。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




