こんにちは!
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(Taylor series)
テイラー展開とは
テイラー展開(厳密にはマクローリン展開)とは、このように任意の関数をべき級数で表したものです。
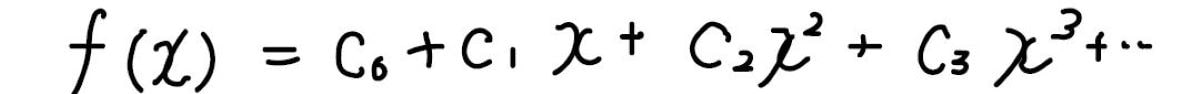
こうすることで、\(x\)がとても小さいときの近似式が導けたり、積分や積分が簡単になったりといったメリットがあります。
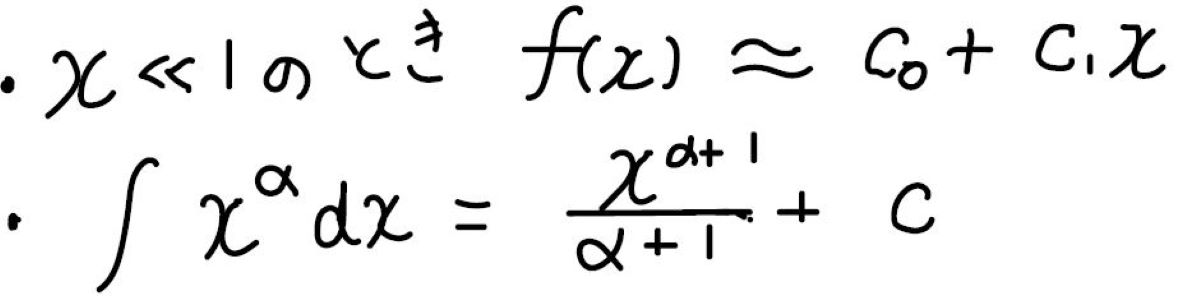
テイラー展開の係数の求め方
ここからは、\(f(x)\)を無限回微分可能な関数と仮定してお話ししていきます。
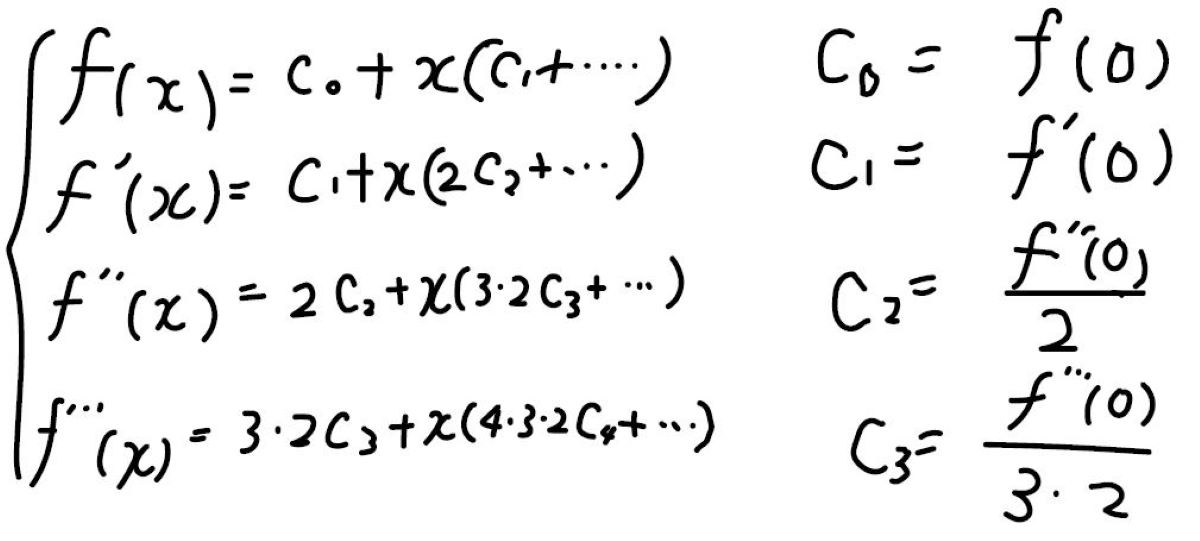
係数の中で一番わかりやすいのは\(C_0\)で、これは\(f(x)\)に\(x=0\)を代入した値になっています。
そして\(C_1\)は、\(f(x)\)の一次導関数に\(x=0\)を代入したものになります。
\(C_2\)はもともと\(x^2\)の項の係数だったので、1回目の微分で\(2\)が係数にかかった値が二次導関数の\(x=0\)の値となります。
そのため、\(C_2\)を求めるためには\(2\)で割る必要があります。
\(C_3\)の場合は、\(3\)もかかるので\(6\)で割ります。
これを階乗を使ってまとめると、この式のようになります。
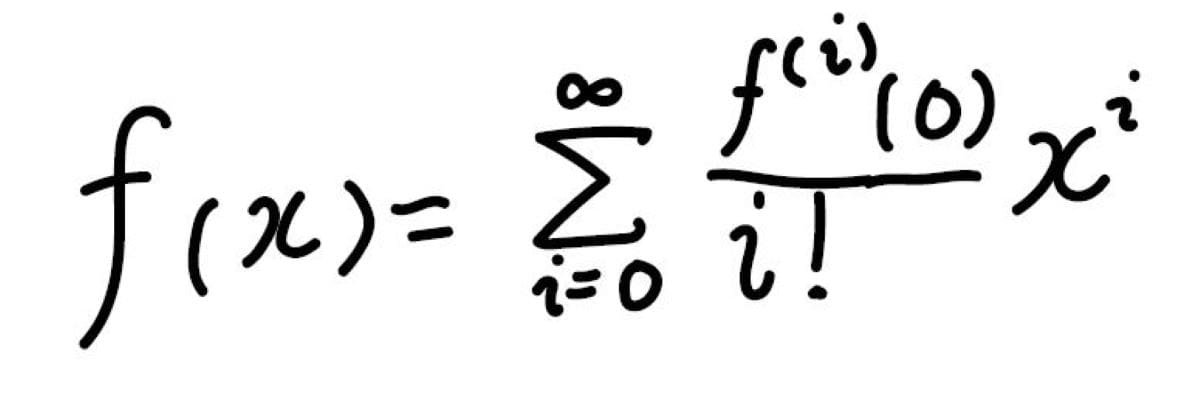
そして、テイラー展開はこのように一般化することができます。
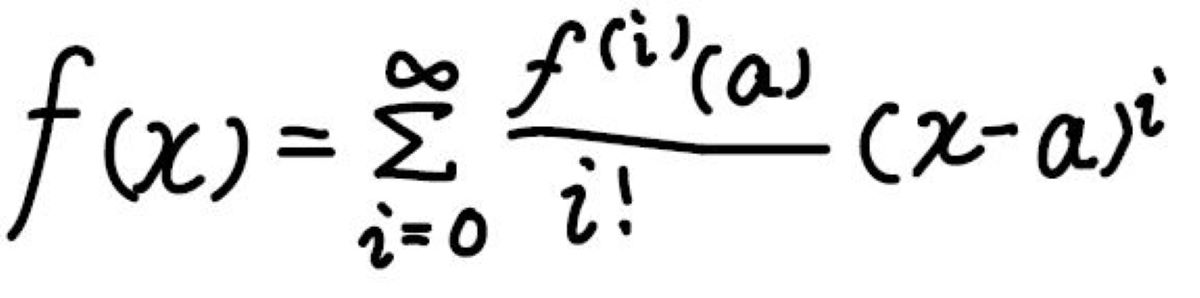
この式では、各項が\(x-a\)の累乗という形になっていて、\(x=a\)を入れることで各係数が求まる構造になっています。
この式を\(x=a\)の周りでのテイラー展開と呼びます。
上の式のように\(a=0\)の周りでのテイラー展開のことは、マクローリン展開といいます。
テイラー展開の例
例として、\(\sin{x}\)、\(\cos{x}\)、\(\rm{e}\)\(^x\)をテイラー展開した式を示します。
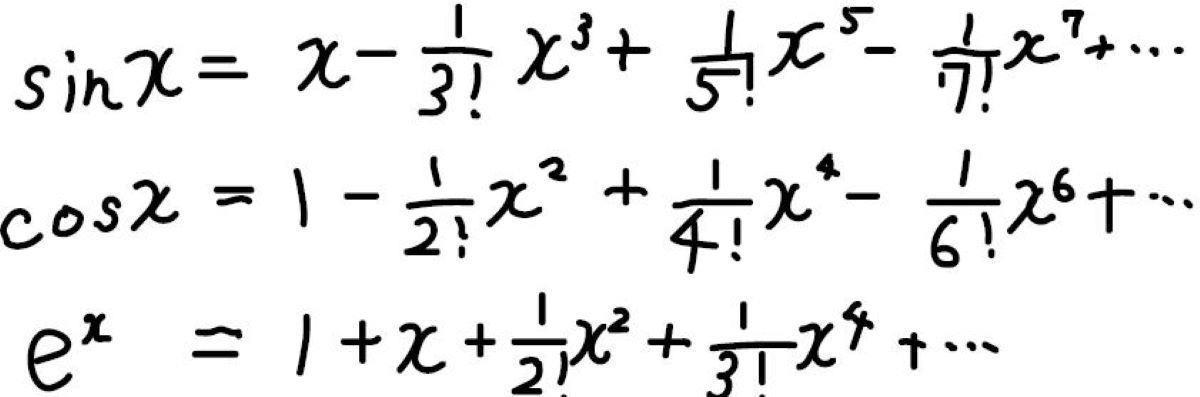
お時間がある方は、実際に微分して確かめて頂ければ、理解が深まると思いますのでぜひやってみてください。
注意点:テイラー展開の等号は成り立たないことがある
そして、最後にテイラー展開には注意すべきことがあるのでそれをお話ししたいと思います。
とても便利に見えるテイラー展開ですが、この等式は常に成り立つわけではありません。
高次の項になるほどその絶対値が大きくなっていく場合、右辺は発散します。
仮に係数がとても大きい場合、\(x\)がとても小さいときしか関数が収束しないように、テイラー展開の式が成り立つかどうかは\(x\)の値によって決まります。
等式が成り立つ\(x\)の範囲を求めるためには、収束半径というものを計算します。
これは、次のような式で定義されます。
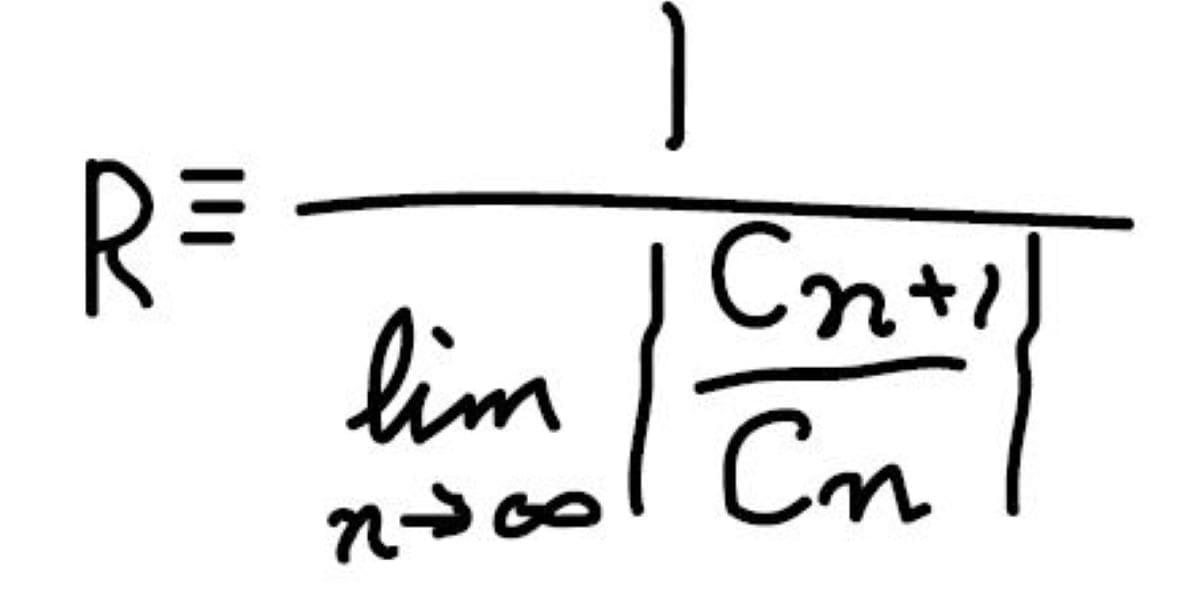
簡単に言葉で説明すると、隣り合う二つの項の係数の比が\(x\)より小さかったら収束していくということです。
\(x\)の絶対値が\(R\)より小さい場合は等式が成立し、大きい場合は右辺が収束しないので等式は成り立たないことになります。
\(x\)の絶対値が\(R\)の場合、必ずしも収束するとは限らず、その関数ごとに実際に代入してみて確かめる必要があります。
その例として\(\displaystyle \frac{1}{1+x}\)を考えてみましょう。
この関数をテイラー展開すると、下のようになります。
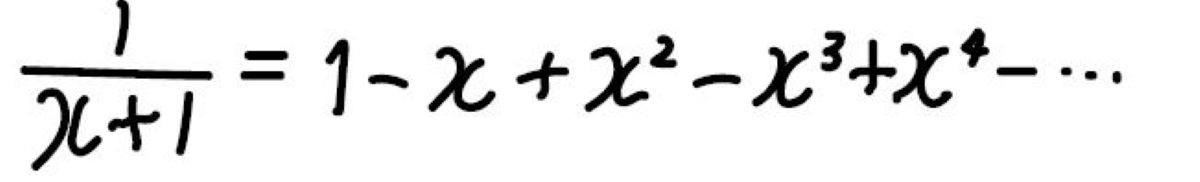
すべての係数が\(1\)なので、収束半径は\(1\)になります。
\(x=-1\)のときは値を持たないので、\(x=1\)のときについて見てみましょう。
そうすると、テイラー展開は\(1-1+1-1+1\)という形になり、どこまで項をとっても\(1/2\)にはならないことがわかります。
よって、このテイラー展開の等式が成り立つ\(x\)の領域は\(-1<x<1\)ということになります。
練習問題
それでは、最後に練習問題をやってみたいと思います。
ここでは複素数のテイラー展開をしてみましょう。
サイエンスでも超重要な式であるオイラーの公式\(\exp{(\rm{i}\mathit{ax})}\)\(=\cos{(ax)}+\rm{i}\)\(\ \sin{(ax)}\)を証明してください。
右辺に\(\sin\)や\(\cos\)があるので、まずは収束半径を求めて、等式が成り立つのだろうかというところから考えてください。
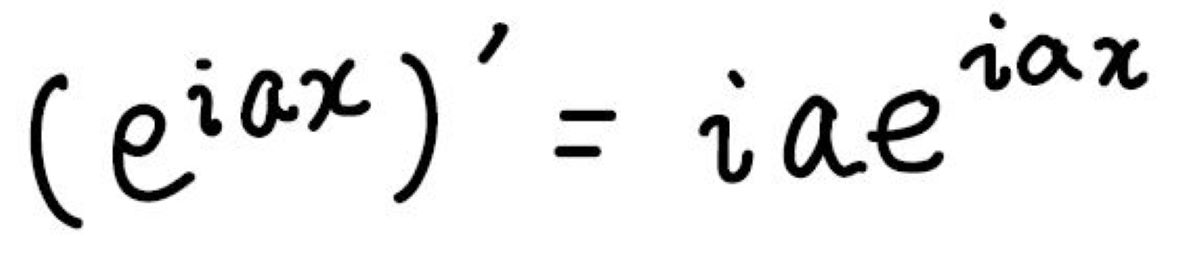
最終的に、このような形まで持っていければOKです。
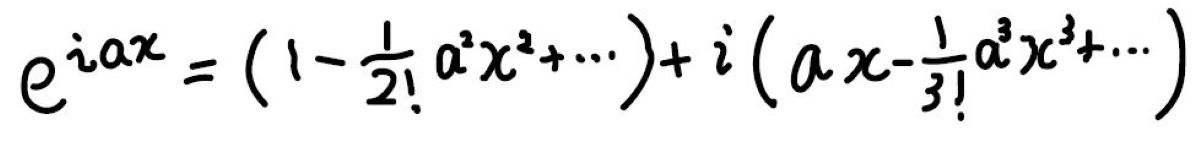
\(\exp x\)の微分は上に書いてあるとおりなので、あとは各項に微分した回数分だけ虚数単位\(\rm{i}\)を掛ければよいことになります。
\(\sin{x}\)と\(\cos{x}\)の収束半径が無限大になることも忘れず確かめておきましょう。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




