こんにちは!
今日は数学の話をやっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(differential equation、differential equation2)
あまり難しい内容は扱わず、サイエンスでもよく使うぐらいの内容に限ってお話ししていきたいと思います。
ではいきましょう!
微分方程式とは
まず、微分方程式とはどういうものかというところから始めます。
例えば、下の式は高校の物理で習うばねの単振動の式ですが、これが微分方程式の例です。

方程式の中に加速度という二階微分が含まれています。
高校物理では\(x\)が\(\sin\)の波で与えられると習いますが、今回はこのように\(x\)を\(t\)の関数として求める方法を説明します。
解法①:両辺を積分する
1つ目の解法は両辺を積分する方法です。
例として、この微分方程式を解いてみます。
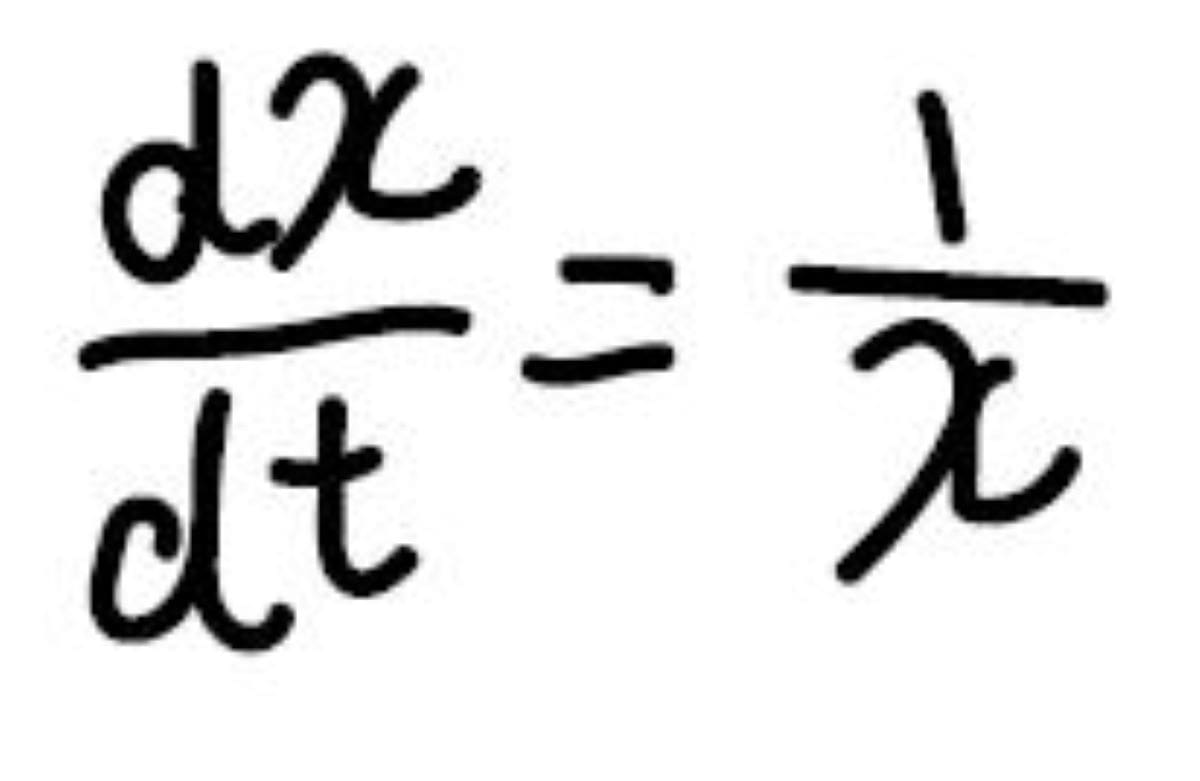
まず始めにすることは、左辺を\(x\)だけの式、右辺を\(t\)だけの式にすることです。
それができたら、両辺を不定積分します。
あとはそれを変形してあげると、下記のように解を得ることができます。
ここで\(C\)は、すべて任意の定数です。
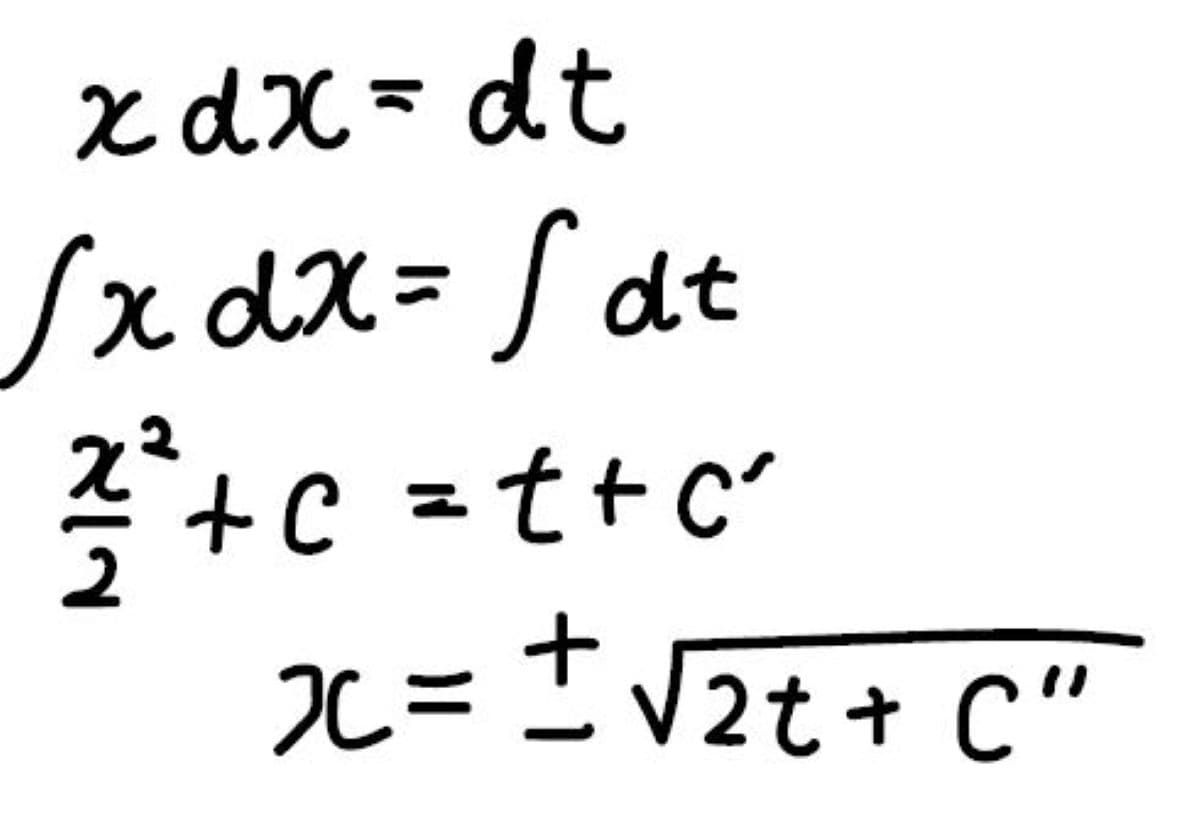
この方法は変数ごとに分けられる場合しか使えないので、次の節では、もっと広く使える解法を紹介します。
解法②:特性方程式を解く
例として、この式を解いてみます。
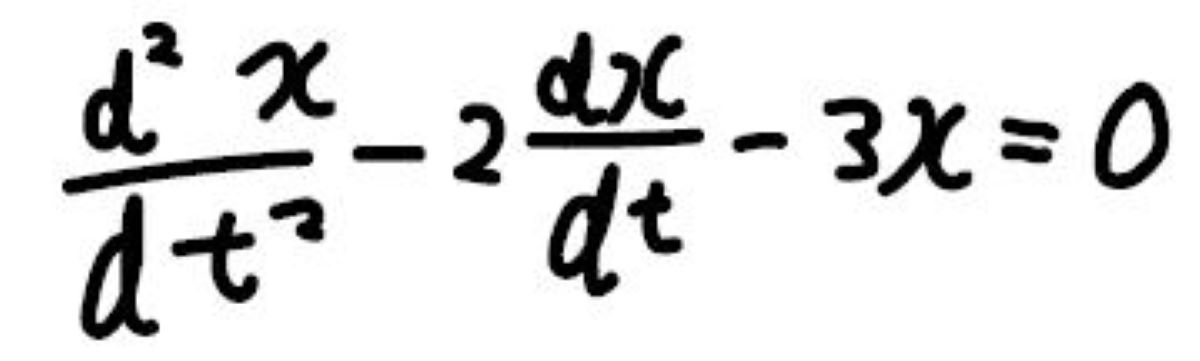
まず、微分方程式からこのような方程式を作ります。
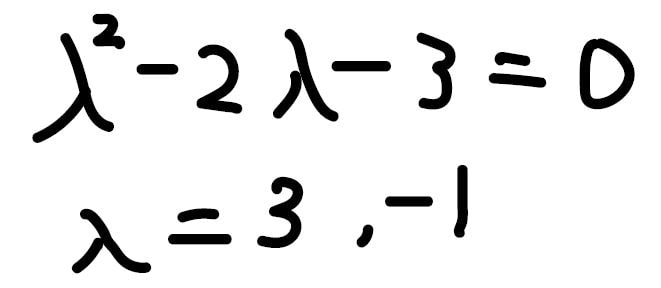
微分した回数分が\(λ\)の指数になるように式を書きます。
\(x\)は\(0\)回微分なので、\(λ\)の\(0\)乗、つまり\(1\)ということで、係数をそのまま持ってきます。
そして、この方程式を解くと\(λ\)の解は\(3\)と\(-1\)と出ました。
この場合、\(x\)の一般解はこのように書くことができます。
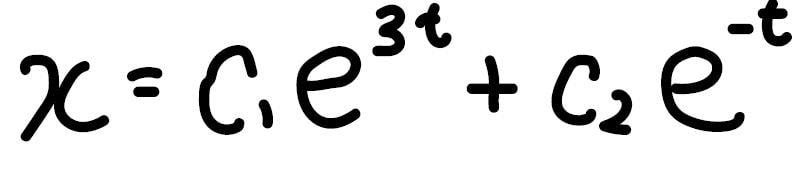
\(e\)の指数部分が\(λt\)になっていて、それらの足し合わせになっています。
本当に方程式を満たしているのか、試しに\(x\)にこれを代入して計算してみると、確かに等式が成り立ちます。
この解き方は慣れれば簡単なので、実際に手を動かしてみることをおすすめします。
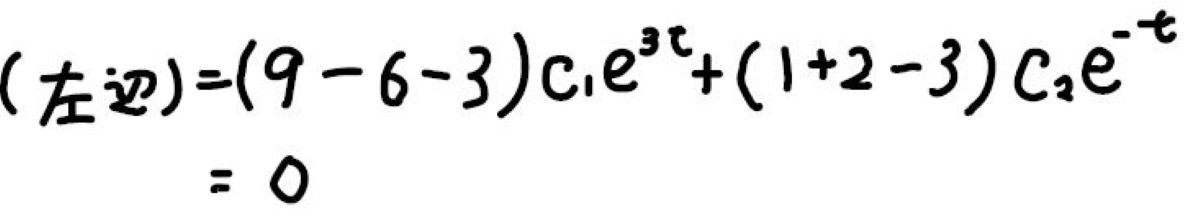
特性方程式が二重解を持つとき
例えば、このような微分方程式があったとします。
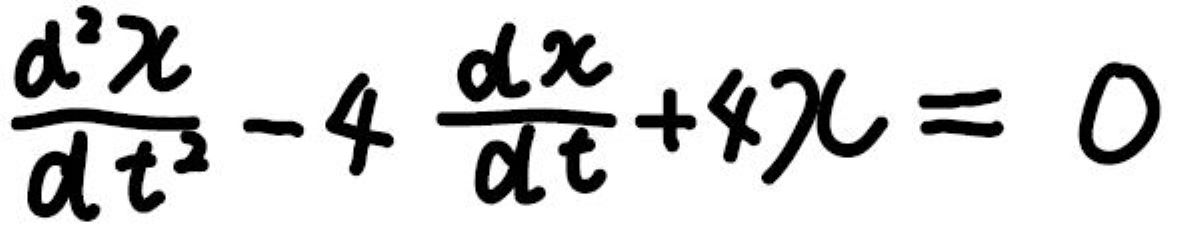
\(λ\)の解は\(2\)のみで、二重解です。

この場合の\(x\)の一般解はこうなります。
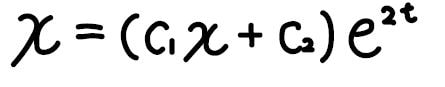
実際に代入してみると確かに、等式は成り立っています。
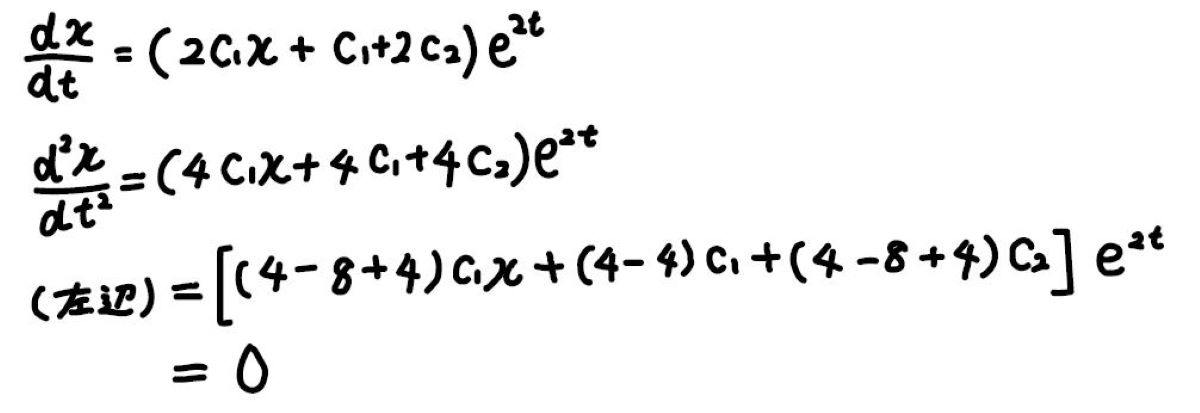
特殊解の求め方
では、少し変わった微分方程式ということで、以下のような形を考えてみます。

変わったことといえば、微分方程式の中に\(3\)という定数が入ってきたことです。
この場合、まず\(3\)を無視して、この形で\(x\)の一般解を求めます。
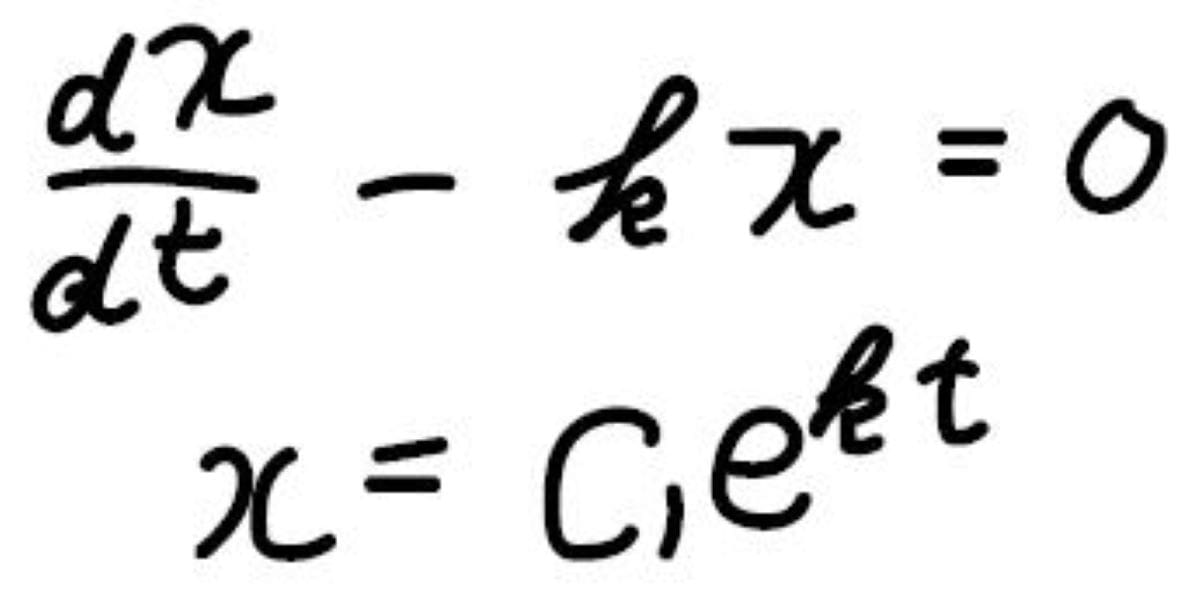
そのあとで、\(3\)を考慮して、このように\(C_2\)という定数項が付くことを考えます。
定数項なら微分しても消えるので、あとは右辺で\(3\)が消えるための\(C_2\)を求めることで\(x\)の式を得ます。
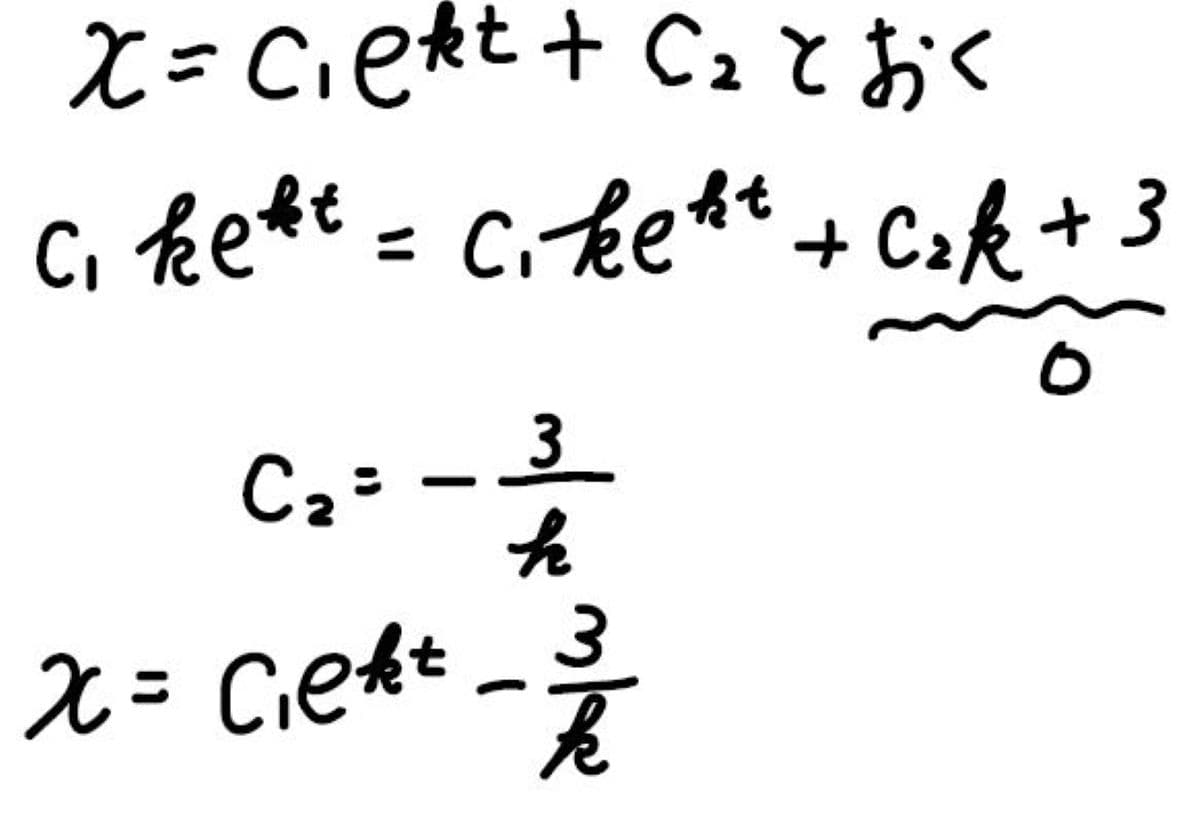
このような解は、特殊解と呼ばれます。
こういう計算は物理や化学、生物でもよく出てくるものなので、できるようにしておきましょう。
練習問題
最後に、練習問題をやって終わります。
物理の問題なので、高校で習っていない方は難しいかもしれませんが、その場合は答えを理解できるまでじっくり見て頂ければと思います。
時刻\(0\)で質量\(m\)の物体を\(h\)という高さから自由落下させました。
物体の速さに比例する空気抵抗(比例定数\(k\))を受けていた場合、時刻\(t\)での物体の位置を\(t\)の関数として表すと、どのような形になるでしょうか?
図で表すと、こちらのようなイメージです。
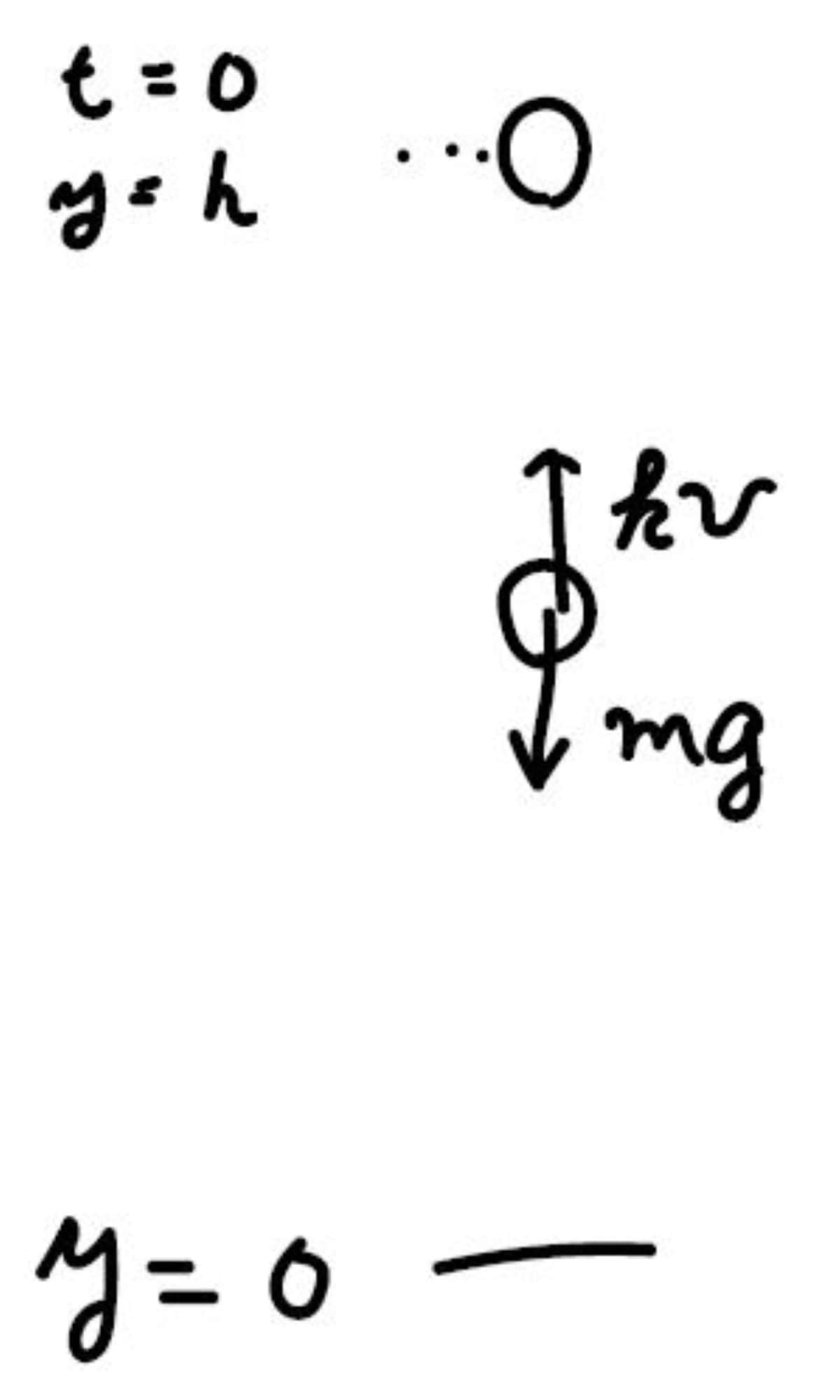
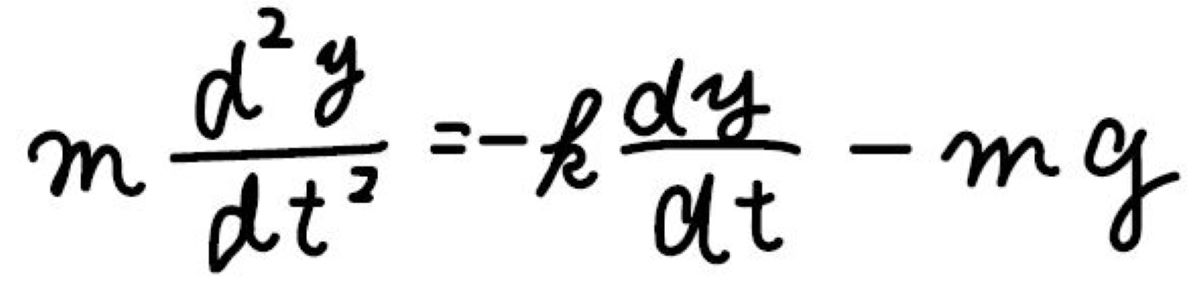
この問題では、2つ初期条件が与えられているので、ただ1つの解が導かれます。
その初期条件とは、時刻\(0\)で\(y=h\)、そして速度は\(0\)だというものです。
最終的に得られる答えは、こちらのとおりです。
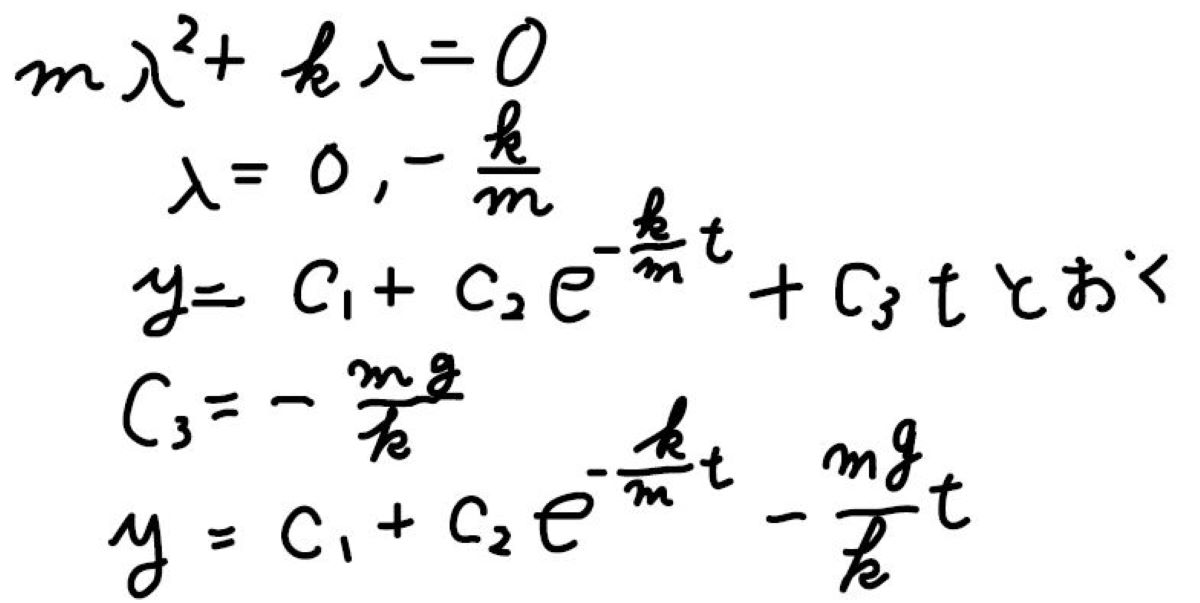
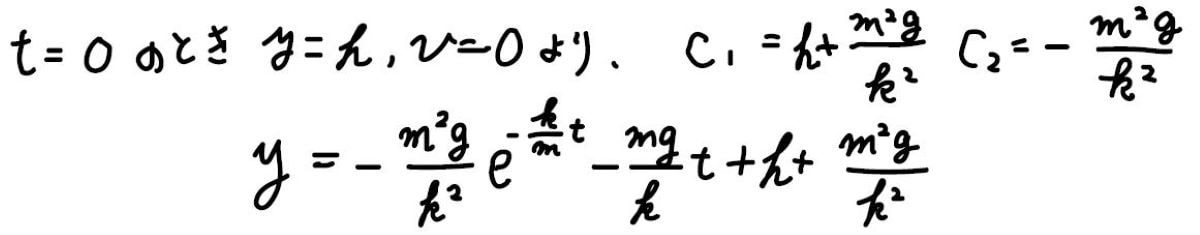
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




