こんにちは!
それでは今回も化学のお話やっていきます。
今日のテーマはこちら!
動画はこちら↓
水素分子についてのハミルトニアン
水素分子は、プロトンが2つと電子が2つの系です
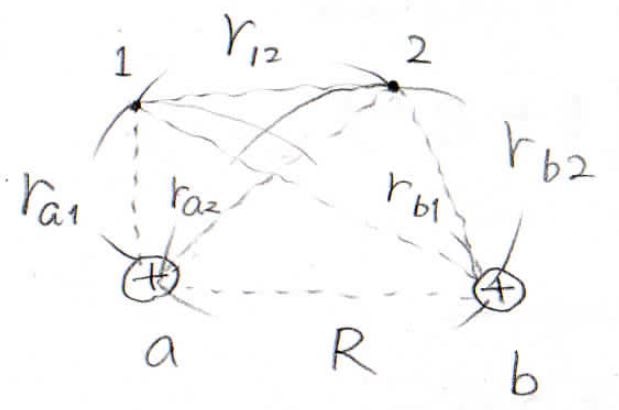
2つの核に\(\rm{a}\)と\(\rm{(b}\)、2つの電子に\(1\)と\(2\)というラベルを付けて、これらを添え字として、図のようにそれぞれの距離を\(r\)で表すことにします。
水素分子イオンのときと同様に、ボルン-オッペンハイマー近似によりプロトンの運動を無視すると、ハミルトニアンはこのように表せることになります。
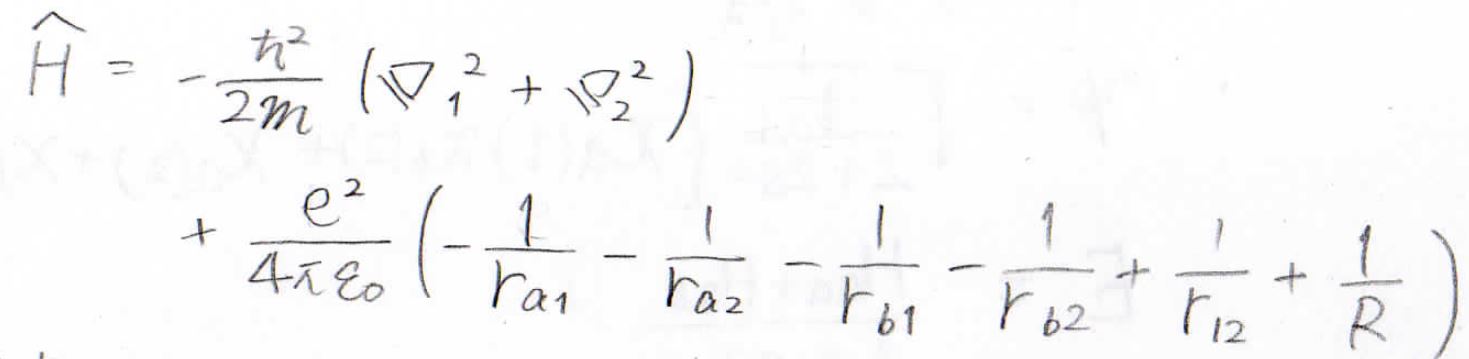
ここで、\(\displaystyle \hbar\)はディラック定数、\(\displaystyle m\)は電子の質量、\(\displaystyle e\)は電気素量、\(\displaystyle \varepsilon_0\)は真空の誘電率です。
水素分子の波動関数の作り方
次に、水素分子の波動関数の形について考えていきます。
ここでは、原子価結合法と分子軌道法という2つの考え方を紹介します。
これらはそれぞれVB法、MO法とも言います。
イメージの違いを軽く説明すると、VB法では水素原子が2個あるように考えます。
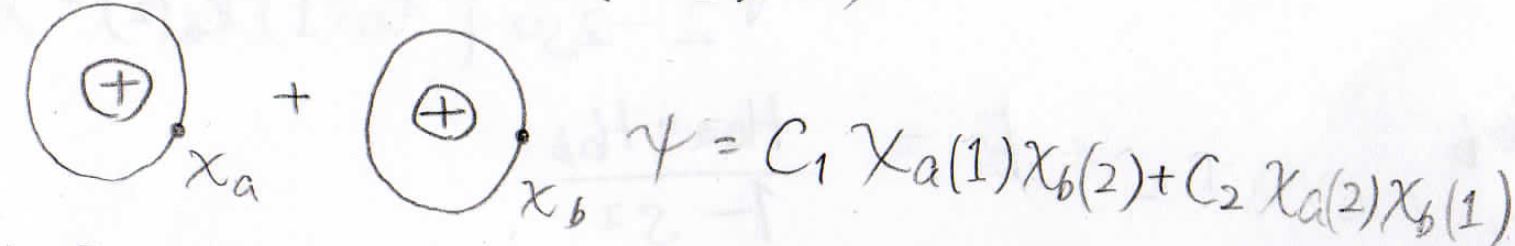
電子の入れ替えも考慮して波動関数を作ります。
対して、MO法では、2個のプロトンに束縛されている電子が2つ共存していると考えて、水素分子イオンの波動関数をもとに水素分子の波動関数を作ります。

MO法については、こちらの記事をご覧ください。

原子価結合法における水素分子の波動関数
ここからは、原子価結合法の計算過程について、お話ししていきます。
\(\chi_\rm{a}\)と\(\chi_\rm{b}\)をそれぞれプロトン\(\rm{a}\)とプロトン\(\rm{b}\)が電子を束縛したとき、すなわち水素原子だったときの波動関数だとします。
水素分子に寄与している構造の中には、\(\rm{a}\)が\(1\)の電子、\(\rm{b}\)が\(2\)の電子を束縛している状態を考えることができます。

このときの波動関数は、この2状態が共存しているという意味で、波動関数の積になります。
また、電子が入れ替わることも考えられます。
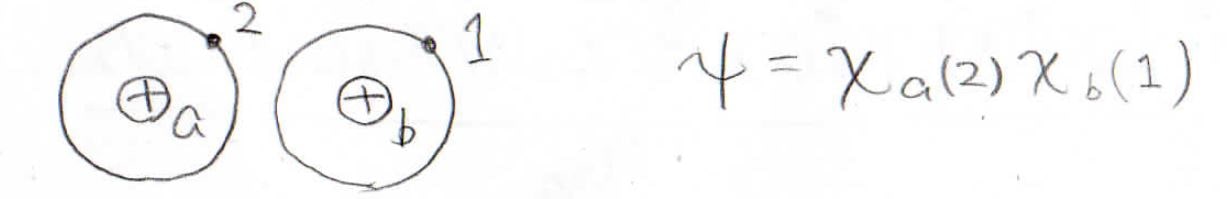
この場合、波動関数は\(\chi_\rm{a}\)\((2)\chi_\rm{b}\)\((1)\)になります。
これらは、水素分子に寄与している個別の状態にすぎないので、水素分子全体の波動関数を一般的に書こうとすると、これらの波動関数の線形結合として、このような形が得られます。
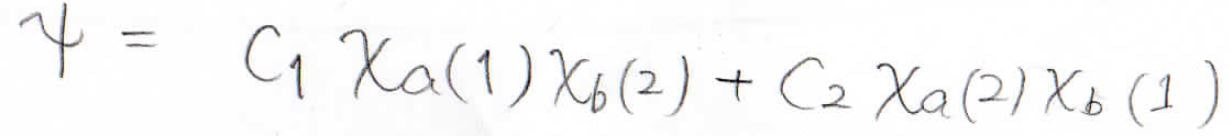
VB法では、この波動関数を試行関数として、変分法によりエネルギーを求めていくことになります。
原子価結合法における水素分子のエネルギー
それでは実際に、エネルギーを考えてみましょう。
エネルギーは下の式で得られますが、まずはその分母から考えます。
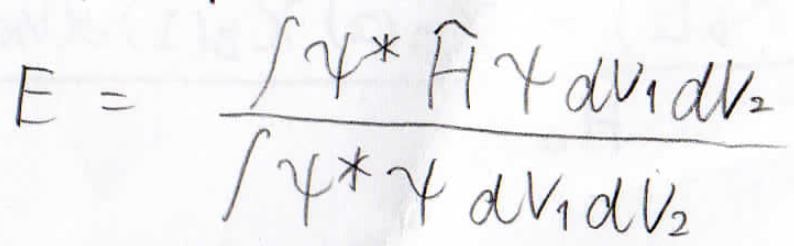
分母を展開すると、このような3つの項が出てきます。
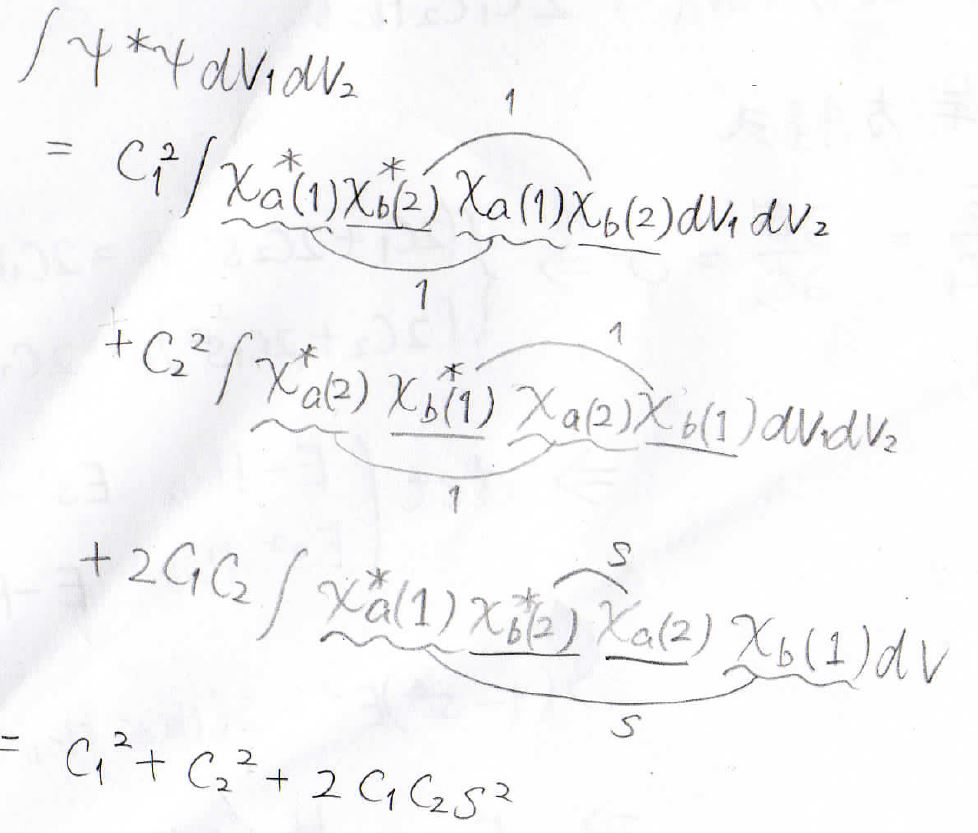
ここで、第一項と第二項の積分部分に着目すると、規格化条件より、線で結んだ2つの原子の波動関数の積の積分が\(1\)になります。
第三項では重なり積分\(\displaystyle s\)が出てきて、結局分母は\(C_1^2+C_2^2+2C_1C_2s^2\)と表されます。
エネルギーの分子側も展開すると、3つの項が出てきて、第一項と第二項の積分部分はどちらも等しくなり、これを\(H_\rm{aa}\)と表すことにします。
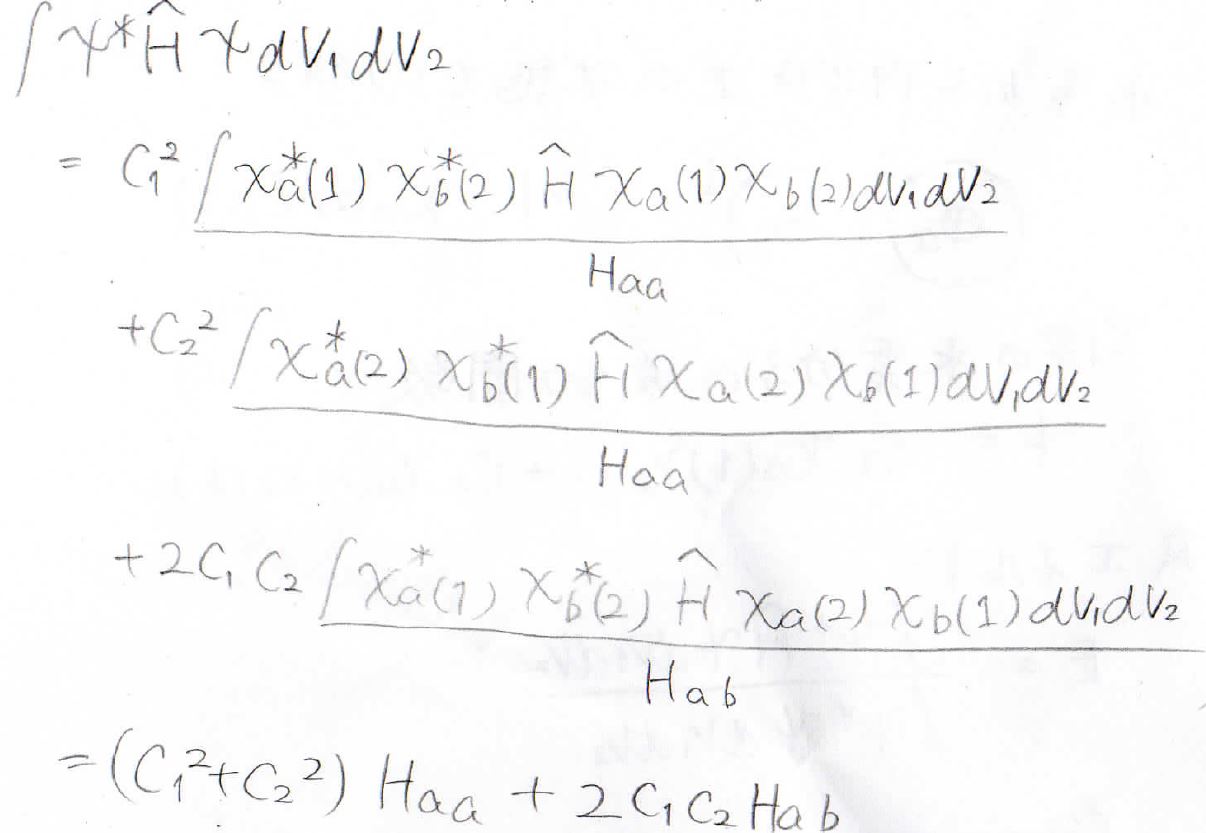
そして、第三項の積分部分を\(H_\rm{ab}\)と置きます。
そうすると、エネルギーも上のように表すことができました。
では最後に、永年方程式を立てて未知定数を決定し、エネルギーを出してみましょう。
まず、微分によってこの2つの関係式が得られます。
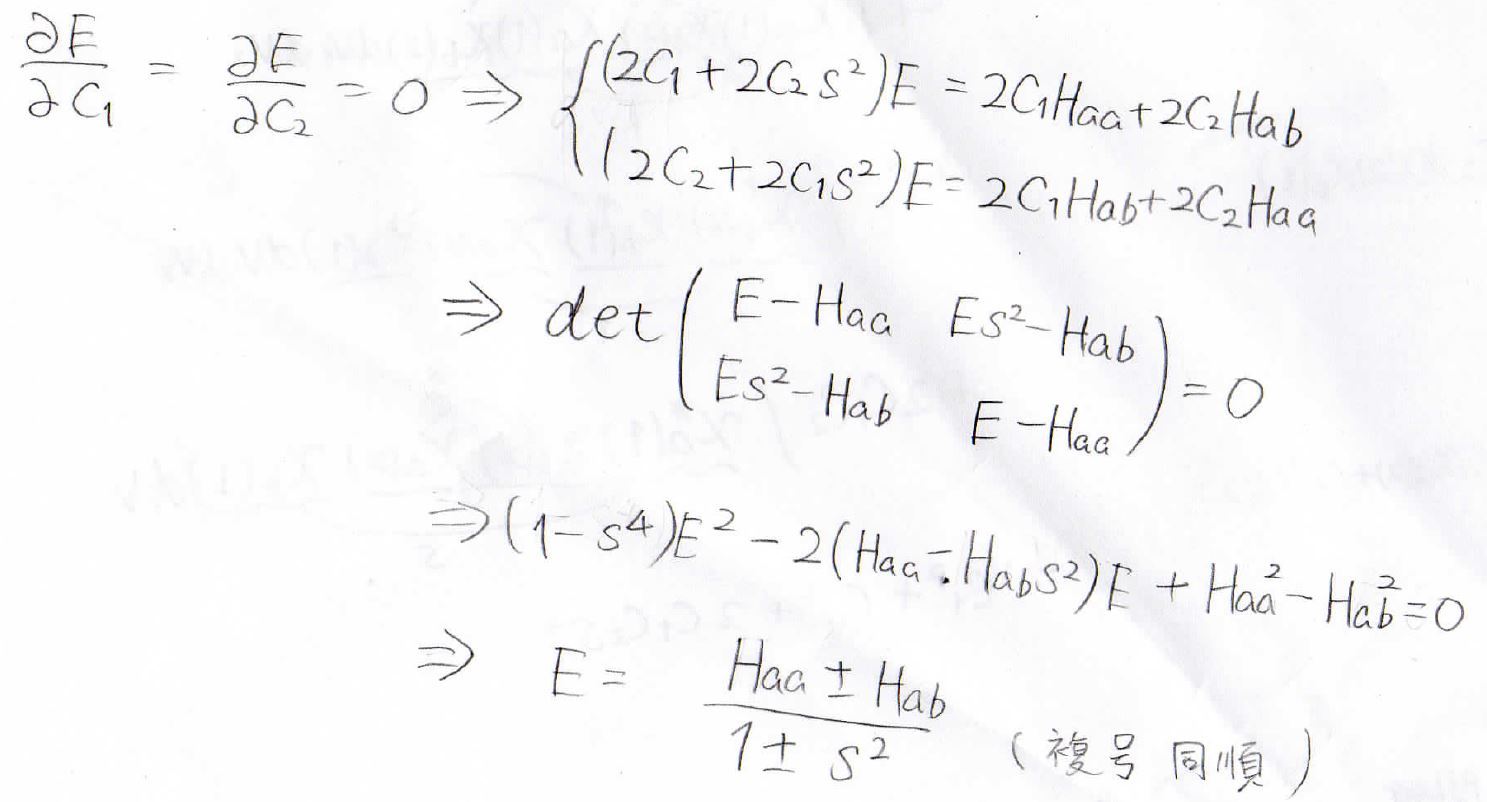
これを整理して行列表記の連立方程式を作り、その係数行列についての行列式が\(0\)になるとします。
その結果、エネルギーが\(\displaystyle \frac{H_\rm{aa}\pm \mathit{H}_\rm{ab}}{1\pm s^2}\)と求められました。
規格化により未知数を消去すると、最終的な答えは、下のようになりました。
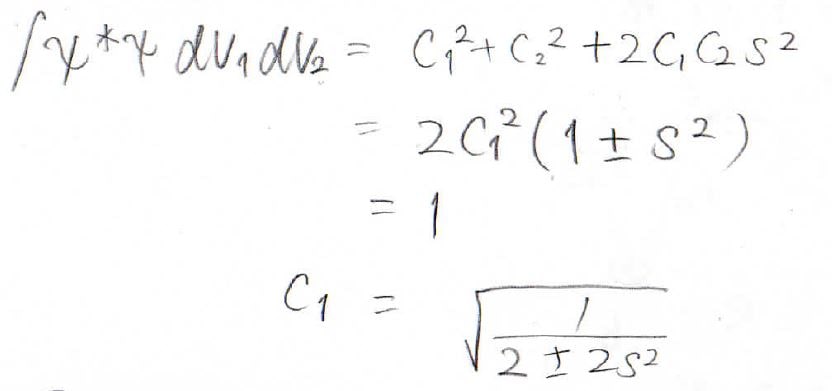
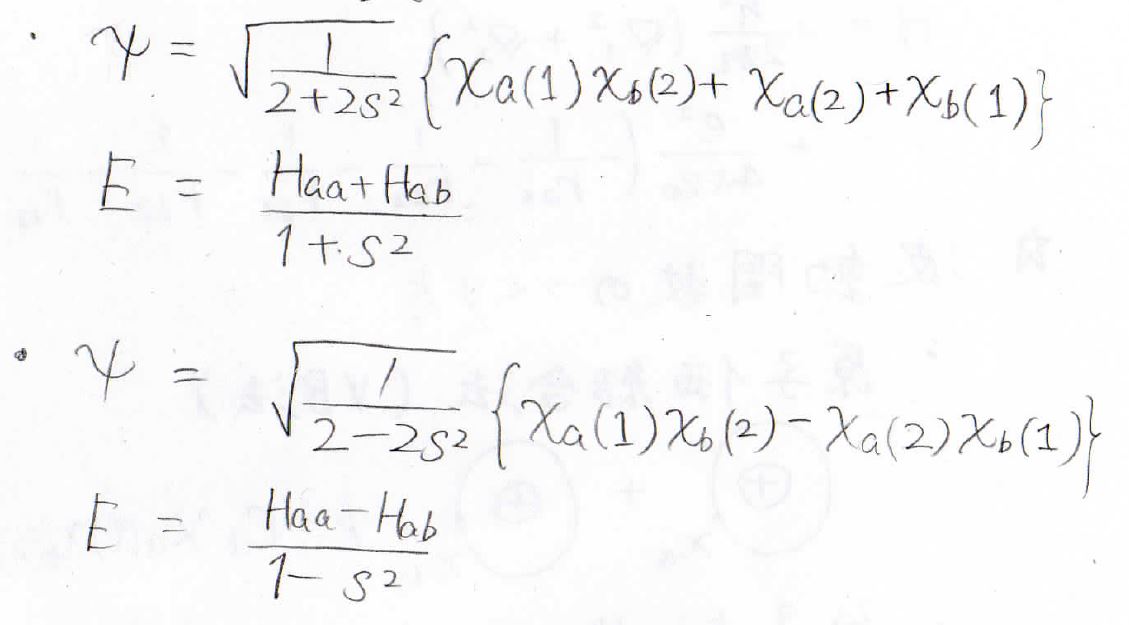
水素分子イオンの式の形とかなり似ている答えが得られました。
ここでやっている計算過程について詳しく知りたい方は、こちらの水素分子イオンについての記事をご覧ください。
変わっているところは、分母の\(s\)が\(s^2\)になっていることと、足し引きする波動関数が積になっていることです。
ハミルトニアンの展開
そして、エネルギーの中に出てきた\(H_\rm{aa}\)と\(H_\rm{ab}\)では、ハミルトニアンをそのままにしていたので、それを展開していきます。
まず、\(H_\rm{aa}\)について展開すると、最終的な答えは\(2E_\rm{H}\)\(\displaystyle +J_1+2J_2+\frac{e^2}{4\pi \varepsilon_0} \frac{1}{R}\)になります。
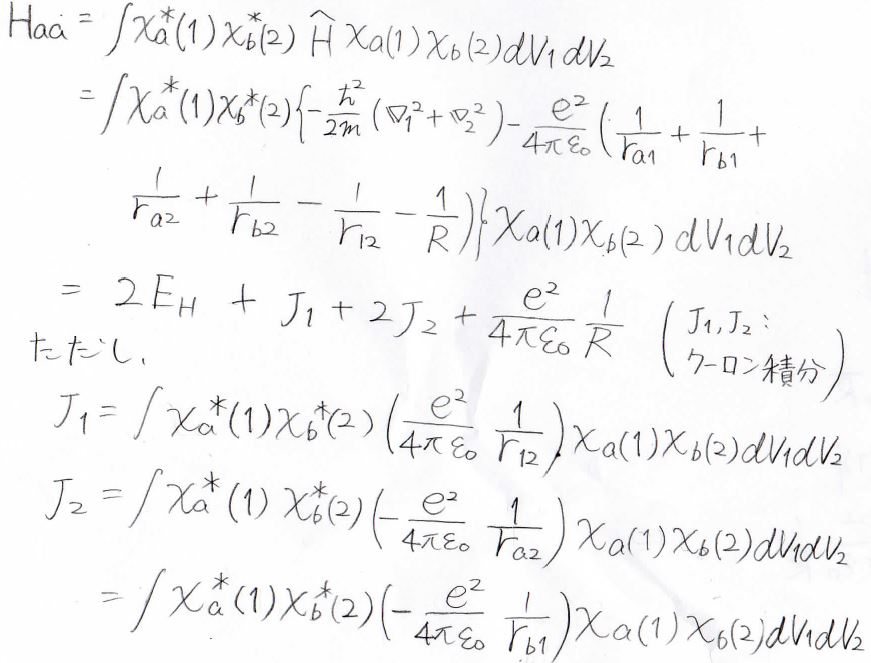
ただし、\(E_\rm{H}\)は水素原子のエネルギーで、\(J_1\)と\(J_2\)はクーロン積分を指します。
\(H_{ab}\)についても同様の変形をすると\(2E_\rm{H}\)\(\displaystyle s^2+K_1+2K_2+\frac{e^2}{4\pi \varepsilon_0} \frac{1}{R}s^2\)になります。
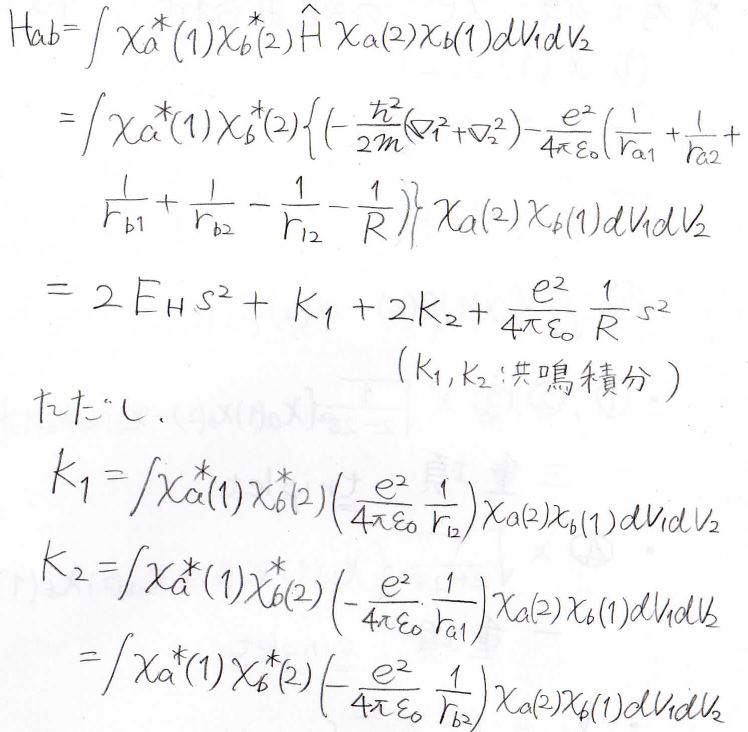
ここで\(K_1\)と\(K_2\)は共鳴積分です。
クーロン積分、共鳴積分の意味については、水素分子イオンの記事を参照してください。

パウリの原理を考慮
さらに、電子はfermi粒子であるため、パウリの原理に従います。
詳しくはこちらの記事、またはその中のpart4の動画をご覧ください。
パウリの原理より、電子を入れ替えたとき、波動関数の位相は反転します。
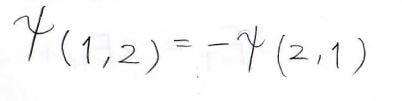
2つの電子のスピンの組み合わせは4通りあり、このようになります。
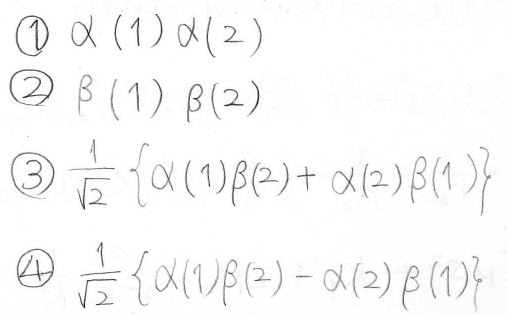
①、②、③は電子を入れ替えたときに元のものと一致してしまう対称なもので、④だけ反対称になっています。
波動関数についても、和をとるものは対称で、差をとるものは反対称になります。
対称な関数と反対称な関数の積は反対称になるため、①、②、③には差をとる形の波動関数をかけて、④には和をとる形の波動関数をかけると、反対称な状態が4つ作れることになります。
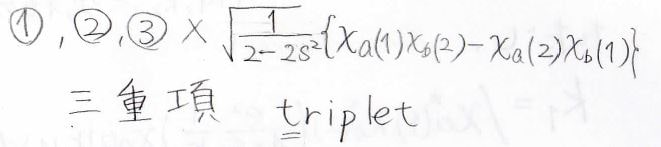
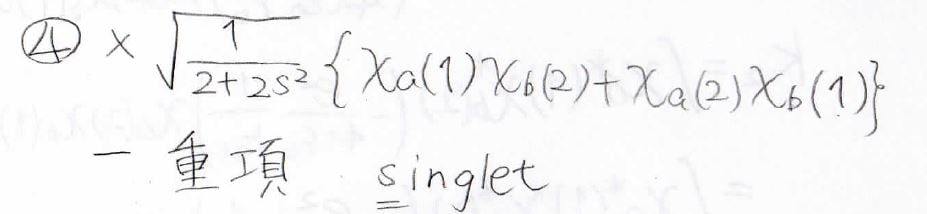
前者についてはスピン状態が3つあるということで三重項と呼び、後者はスピン状態が1つしかないので一重項と呼びます。
それぞれ、triplet、singletと言うので、\(\displaystyle \rm{T}\)と\(\displaystyle \rm{S}\)を添え字にすると、最終的に得られる波動関数とエネルギーの解は、下のようになります。
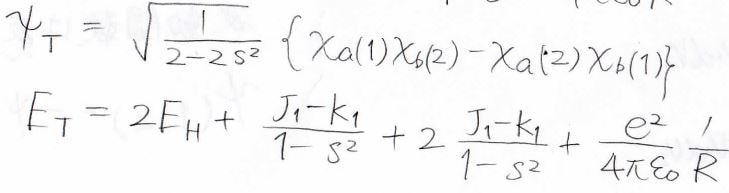
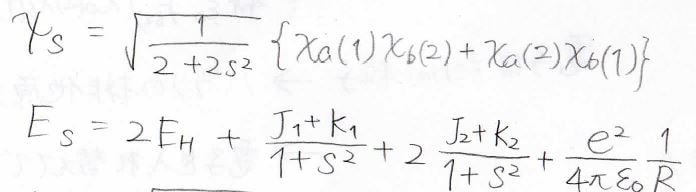
最後にエネルギーの核間距離依存性を見ると、一重項が安定な状態で三重項が不安定な状態であることがわかります。
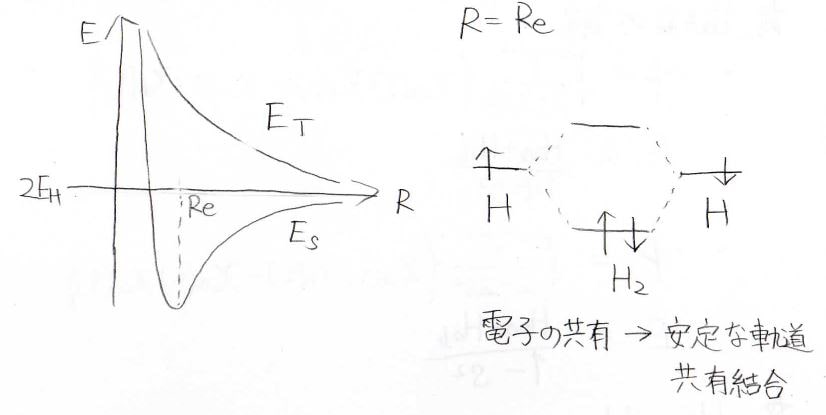
平行核間距離を\(R_\rm{e}\)として、\(\displaystyle R=R_\rm{e}\)におけるエネルギーを見ると、右のようになります。
両脇が水素原子のエネルギーで、この2状態から水素分子になることで安定な軌道と不安定な軌道ができ、安定な軌道に電子が入ることで原子のときよりも安定になります。
これが共有結合が形成される原理です。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!





