こんにちは!それでは今回も化学のお話やっていきます。
今日のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(spin-spin coupling)
それでは内容に入っていきます!
前回までのおさらい
まず、前回までのおさらいです。
NMRとは核磁気共鳴というもので、磁場をかけて2状態にゼーマン分裂した核スピンが特定の電磁波の吸収により共鳴する現象のことを言います。
この共鳴振動数は近くにどんな官能基があるのかということ、外部磁場の大きさによってきまります。
官能基の推定のためには外部磁場によらない物理定数の方が都合がよいため、化学シフトという値を使います。

標準物質としてテトラメチルシランを使い、そのピークと目的のピークの共鳴振動数の差を分光計の振動数で割ったものが化学シフトです。
そして、化学的に等価である複数の原子核については化学シフトの値が同じになります。
化学的に等価であるかどうかを決めるのは、回転対称、鏡面対称、そして配座の交換による平均化という要素になります。
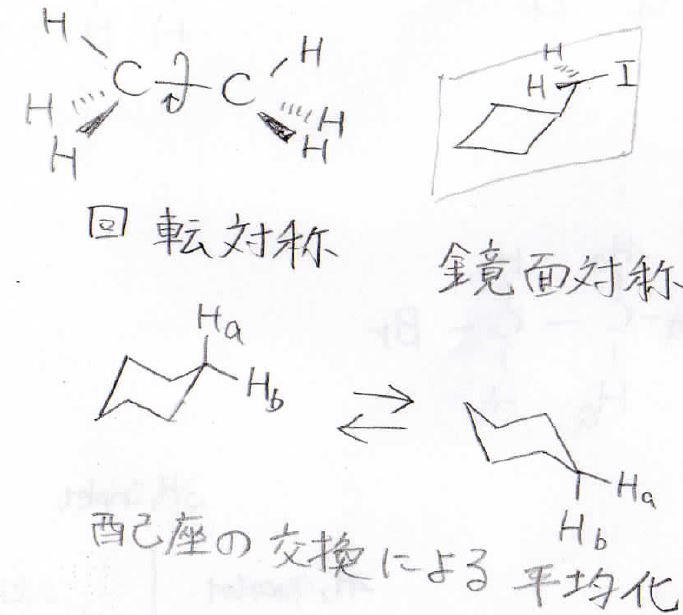
等価な水素の個数分だけスペクトルのピークが大きく出るので、そこから等価な水素の個数比を求めることができます。
詳しくはこちらの記事をご覧ください。



隣接する水素の影響
それでは、新しい内容に入っていきます。
原子核が感じる実質の磁場の大きさは電子由来の局部磁場に影響されるんですが、実は近くにある原子核のスピンにも影響されます。
例えば2つの水素原子HaとHbがこのような位置関係にあったとします。
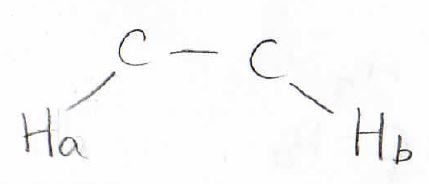
まず、Haのスピン状態が2つに分かれたとします。
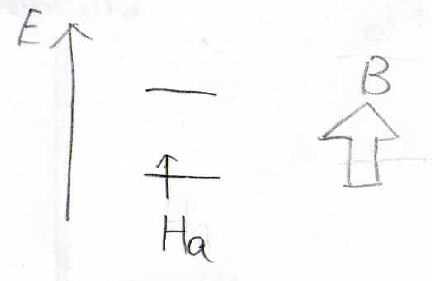
その状態でHbの状態について考えてみます。

Haの核スピンが影響するとすると、Haのスピンの向きにより微妙に磁場の大きさが変わってきます。
\(h_a\)というのがHbの核がHaの核から受ける磁場の大きさで、Haのスピンが外部磁場と順平行な場合は磁場が大きくなるので、ゼーマン分裂の幅が大きくなります。
逆向きの場合は、反対にゼーマン分裂の幅が小さくなります。
結果として、1個の水素原子に対応するピークだったとしてもこのように2本のピークが現れることになります。

この現象をスピン-スピン分裂といいます。
隣接水素が複数個ある場合
そして、もうちょっと一般的な例として、隣接する水素が複数個ある場合についても考えてみましょう。
まず、隣接水素が2個ある場合は、両方が下向き、両方が上向き、どちらか片方だけが上向きというこの4通りが考えられます。

それで一方が上向きでもう一方が下向きのこの2状態については発生させる磁場の大きさに違いがありませんので、結局ピークは3本に分かれることになります。
真ん中のピークだけは2状態に対応しているので、両端のピークより高いピークとなり、その積分比は1:2:1になります。
隣接水素が3個ある場合はこのようになり、ピークの本数は4本、その積分比は1:3:3:1になります。

これを一般化したのがこちらの表になります。

一般的にピークの本数は等価な隣接水素の個数より1だけ多くできるという\(N+1\)則に従います。
そして、ピークの積分比はこのようにパスカルの三角形で表すことができます。
そしてこの別れ方には呼び方がついてまして、一重線はsinglet、二重線はdoublet、三重線はtripletといいます。
カップリング定数
そしてここまでが別れ方の話でしたが、分かれる幅も重要なパラメータになります。
まず、複数に分裂したピークの間隔は等間隔になりまして、その幅に対応する周波数の差をカップリング定数といい、多くの場合、大文字の\(J\)で表します。
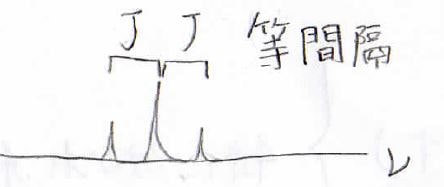
このカップリング定数は着目している水素と隣接水素の位置関係によって決まっていて、例えば先ほど考えたものと同じこのビシナルカップリングでは\(J\)が\(6\)~\(8 \rm{Hz}\)となることが知られています。

こっちのジェミナルカップリングでは\(J\)は化合物によって大きく変化し、\(0\)~\(18 \rm{Hz}\)となります。
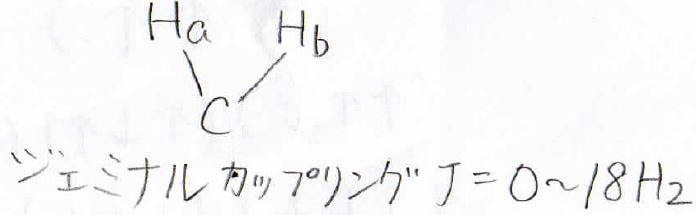
この効果は位置関係が遠いほど効きにくいので、この1,3-カップリングでは目で確認できるほど大きな分裂は起こらず、\(J\)はほとんど\(0\)になります。

NMRスペクトルからカップリング定数を計算する場合には化学シフトでの幅を分光計の周波数をかけてあげればいいので、これもぜひ覚えておいてください。

今回やった内容は基礎的な場合のみでして、もっと複雑なスピン-スピン分裂もありますので、それについては次のNMRの記事でお話ししていきますので、そちらもぜひ見てください。
練習問題
それでは内容は以上なので、練習問題をやってみましょう。
こちらのブロモエタンと2-ヨードプロパンのNMRスペクトルを予測してくださいというのが問題です。
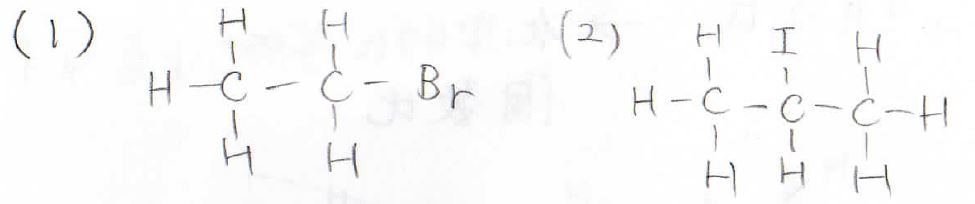
まずは等価な水素が何組あるか考えてみて、スペクトルを書いたら各ピークがどの水素に帰属しているのかも分かるように積分比を書くなり、HaやHbなどと名前を付けるなりしてください。

3個の水素に対応するピークは\(1\)~\(2 \rm{ppm}\)の範囲に現れ、隣接水素が2個あるので\(2+1\)でtripletになります。
2個の水素に対応するピークはブロモ基の反遮蔽化により\(3\)~\(4 \rm{ppm}\)の範囲に現れます。
隣接する水素は3個なのでquartetになります。
続いて、(2)の2-ヨードプロパンのスペクトルはこのようになります。

等価な水素原子の組み合わせは2組あり、6個の水素に対応するピークは\(1\)~\(2 \rm{ppm}\)の範囲に現れます。
隣接水素は1個なので、doubletになります。
そして、1個の水素原子に対応するピークは\(3\)~\(4 \rm{ppm}\)の範囲に現れ、隣接水素が6個もあるので七重線、septetになります。
まとめ
はい、それでは軽くおさらいをやって終わります。
今回はスピン-スピン分裂というものについてお話ししました。
これは着目している水素と等価ではない水素が隣接している場合に起こる現象で、近くの原子核によってできる磁場の影響がその原因です。
一般的には分裂後のピークの本数は隣接水素の数+1になるという\(N+1\)則が成り立ちまして、各ピークの積分比はパスカルの三角形から分かります。
分裂の幅はカップリング定数と呼ばれ、水素原子同士の位置関係が大きく関係しています。
各ピークの間隔は等間隔になります。
カップリング定数はNMRスペクトルにおける化学シフトの変化幅に分光計の周波数をかけることで求めることができます。
もっと複雑なスピンスピン分裂については次のNMR動画でお話ししますので、そちらも見ていただけると嬉しいです。
それではどうもありがとうございました!