こんにちは!
今回も化学の話をしていきます。
今回のテーマはこちら!
水素分子イオンは、水素分子\(\displaystyle \rm{H_2}\)から電子が1個抜けて、プロトンが2個と電子が1個の系です。

動画はこちら↓
動画で使ったシートはこちら(hydrogen molecule ion 1、hydrogen molecule ion 2)
水素分子イオンの系
まず、水素分子イオンの系を詳しく見ていきます。
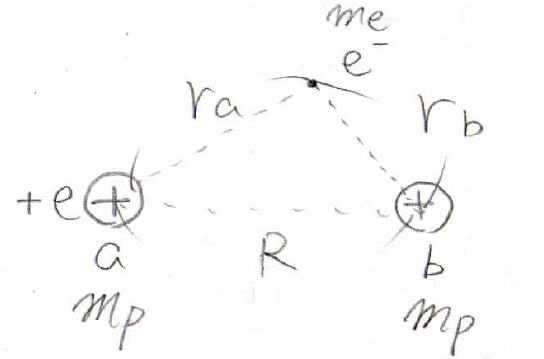
プロトン2個に\(\rm{a}\)と\(\rm{b}\)というラベルを付けて、プロトンの質量を\(m_\rm{p}\)、電子の質量を\(m_\rm{e}\)と表すことにします。
\(\rm{a}\)のプロトンと電子との距離を\(r_\rm{a}\)、\(\rm{b}\)と電子との距離を\(r_\rm{b}\)、プロトン間の距離を大文字の\(R\)で表すことにします。
この場合、全エネルギーを導くためのハミルトニアンは、量子の多体問題になるため、厳密に解くことはできません。
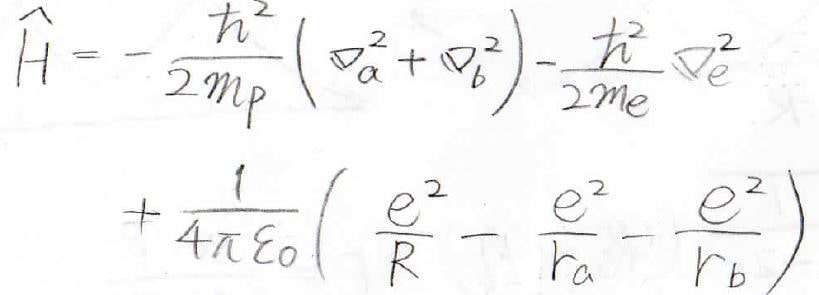
そこで、ボルン=オッペンハイマー近似により、電子よりも質量がとても大きいプロトンの運動は止まっていると考えます。
これで、電子の動きだけを考えればよいことになります。
水素分子イオンの波動関数
ここからは、水素分子イオンの波動関数を考えていきます。
変分法で計算する試行関数は、次のように考えます。
2つのプロトンで1個の電子を共有している状態は、どちらか一方が電子を取り込んだこの2状態が混ざったものであり、全体の波動関数は各状態の波動関数の線形結合で与えられるものとします。
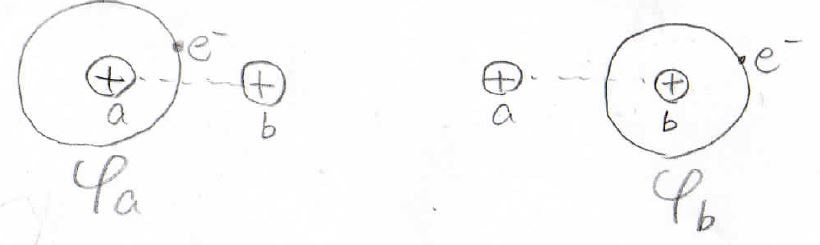
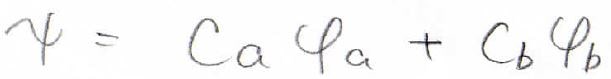
この考え方は、LCAO(Linear Combination of Atomic Orbitals)近似と言います。
ここで、\(\varphi _\rm{a}\)と\(\varphi _\rm{b}\)は水素原子の波動関数です。
より現実に近い計算をするなら、水素原子のすべての波動関数について考えるべきですが、ここでは簡単のため、最も寄与が大きいと思われる基底状態、すなわち\(\displaystyle 1\rm{s}\)軌道のみの寄与を考えることにします。
水素原子の基底状態の波動関数は、こちらの式になります。
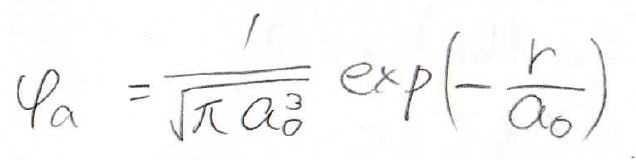
詳しくは、こちらの水素原子の軌道計算の記事か変分法による計算の記事を見てください。

水素分子イオンのエネルギー
次に、この波動関数を使ってエネルギーを求めていきます。
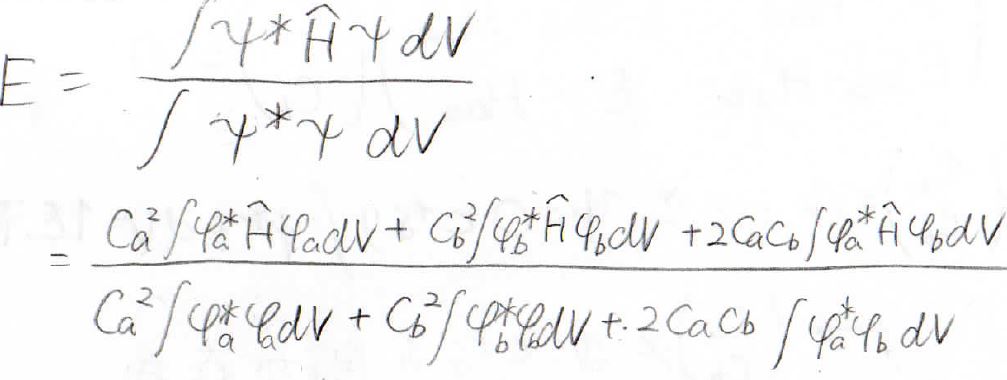
2つのプロトンは便宜上、\(\rm{a}\)、\(\rm{b}\)というラベルをつけていますが、本来区別することはできないので、下のような関係が成り立ちます。
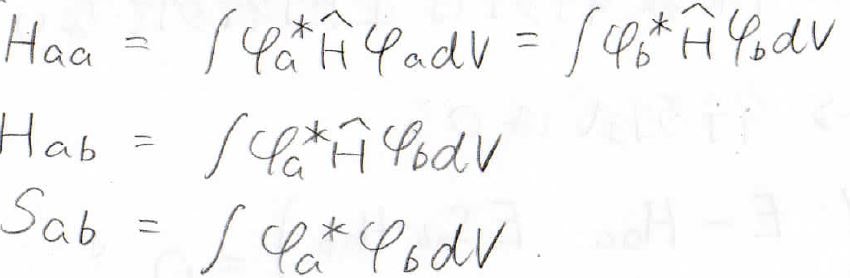
これを未知数で微分して、極小を求めていきます。
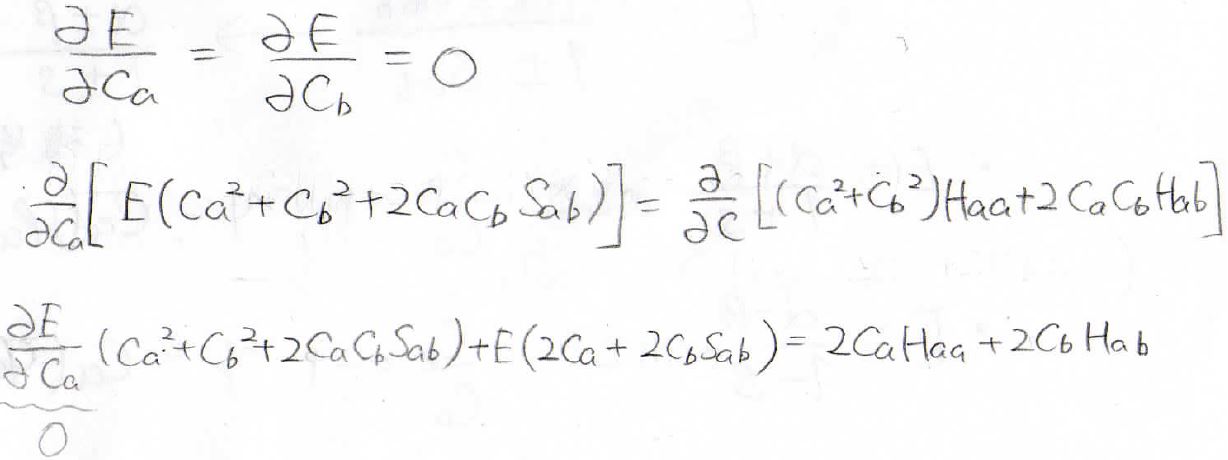
今回は\(C_\rm{a}\)、\(C_\rm{b}\)という2つの未知数があるので、連立方程式が得られます。
連立方程式は、行列で表現できます。
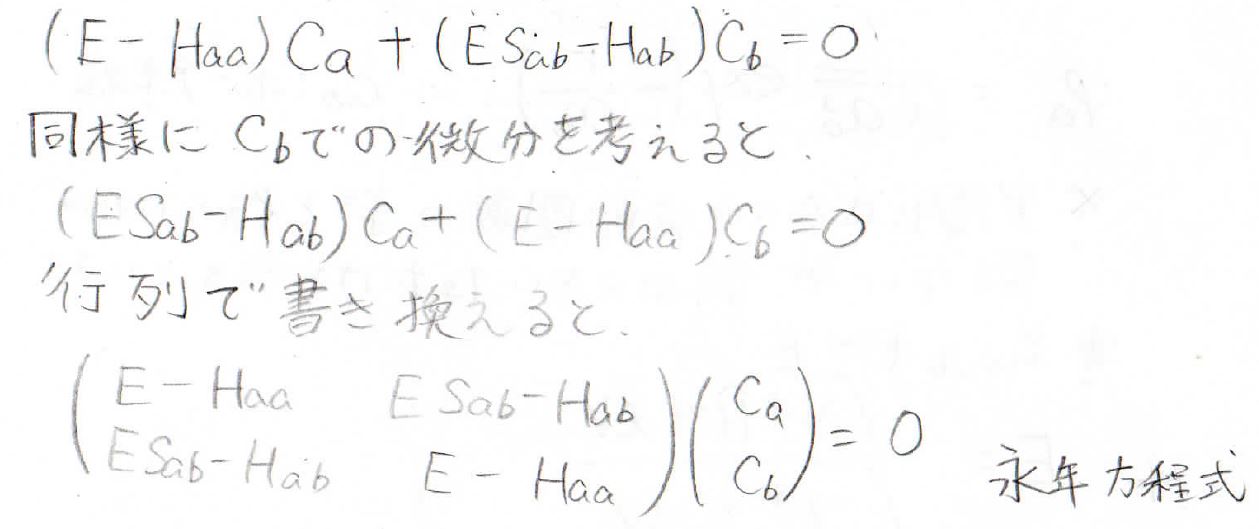
この方程式を永年方程式と言います。
この連立方程式において、\(C_\rm{a}\)、\(C_\rm{b}\)がともに\(0\)というのが一番簡単な答えですが、それだと\(\psi=0\)になって、規格化条件を満たしません。

そのため、\(C_a=C_b=0\)以外の解があることになり、係数行列は正則行列ではないことがわかります。
したがって、その行列式は\(0\)になります。
正則行列の性質については、こちらを参照してください。

行列について基本的なことも解説しておりますので、それらの記事も貼っておきます。




そして、行列式が\(0\)になることより、エネルギーを下のように求めることができました。
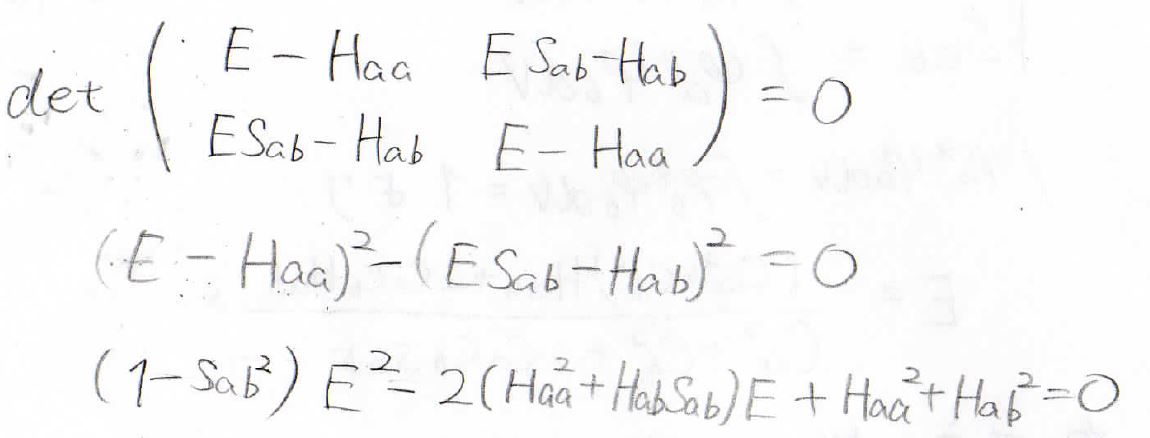
ここで、\(H_\rm{aa}\)を\(\alpha\)、\(H_\rm{ab}\)を\(\beta\)、\(S_\rm{ab}\)を\(s\)と表すことにします。

エネルギーが\(\displaystyle \frac{\alpha+\beta}{1+s}\)であるときには、\(C_\rm{a}\)と\(C_\rm{b}\)は同符号になり、波動関数は波動関数の足し算になります。
エネルギーが\(\displaystyle \frac{\alpha-\beta}{1-s}\)のときには、\(C_\rm{a}\)と\(C_\rm{b}\)は異符号になるので、波動関数は波動関数の引き算になります。
これを規格化することで\(C_\rm{a}\)の値を求めることができ、波動関数とエネルギーを未知数がない形で、2通り求めることができました。
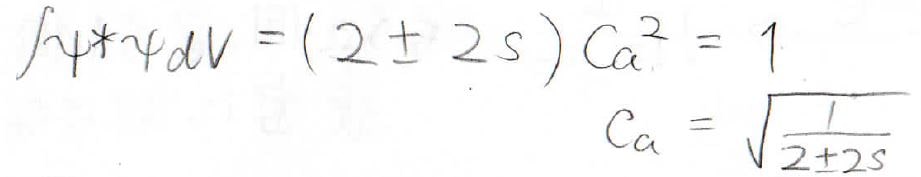
ここに書いた図は、波動関数の位相を表しており、右側がこれらを足した水素分子イオンの波動関数を表します。
両者を比べると、上側では位相が常に正になっていますが、下側では中心で位相が反転しています。
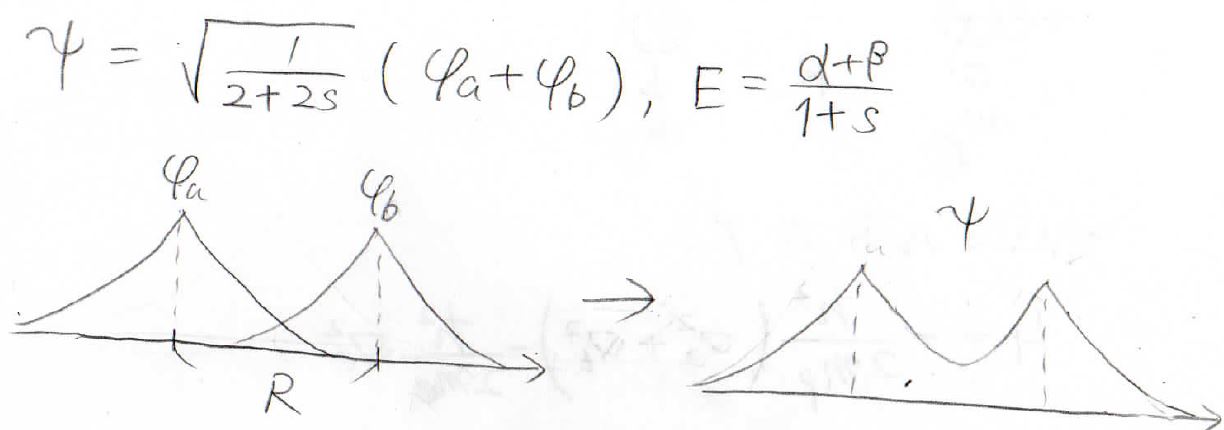
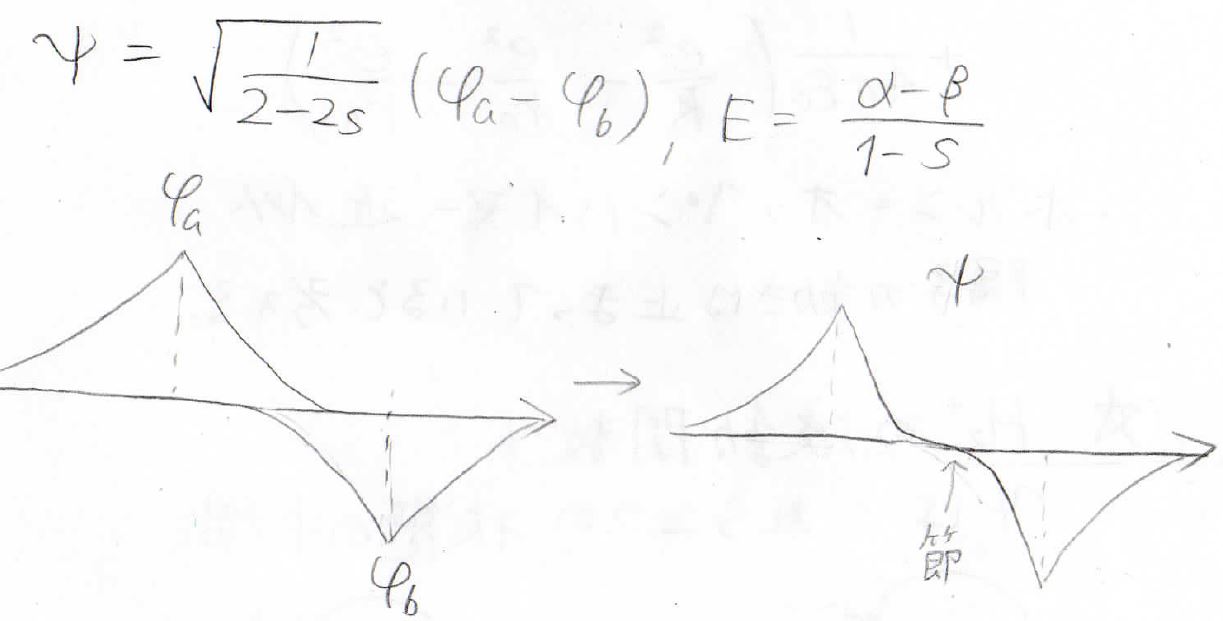
このように波動関数の符号が入れ替わる部分は節と言われ、これが結合のあり方やエネルギーを考えるうえで重要になってきます。
\(\alpha\)、\(\beta\)、\(s\)について
ここからは、この式に入っている\(\alpha\)、\(\beta\)、\(s\)について、詳しく見ていきます。
\(s\)
まず\(s\)ですが、これには名前がついており、重なり積分と言います。
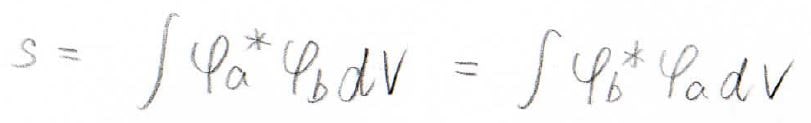
物理的な意味は、2つの波動関数でどのくらい重なっているのかというものです。
まったく重なってないときには\(s=0\)、完全に重なっているときには、規格化条件より\(s=1\)になります。
どれくらい重なるのかは2つのプロトン間距離と対称性に依存し、いまの場合は\(R\)が小さいほど\(s\)は大きな値になります。
\(\alpha\)
続いて、\(\alpha\)も見ていきます。
ハミルトニアンを分解すると、下のような3つの項に分けることができるのですが、その第一項は水素原子のエネルギーになっています。

ここでは、第一項を\(E_\rm{H}\)と置くことにします。
そして、第二項は\(J\)と置いておきます。
最後の第三項は、プロトン間の静電反発のポテンシャルエネルギーで、電子の運動とはまったく関係がありません。
結果として、\(\displaystyle \alpha=E_H+J+\frac{1}{4\pi\varepsilon}\frac{e^2}{R}\)と変形できます。
\(\beta\)
同様のことを\(\beta\)についてもやってみます。
まず、第一項を見ますとこのハミルトニアンは\(\rm{b}\)が水素原子だったときのエネルギーですので、書き換えて\(E_\rm{H}\)を前に取り出すことで結局\(E_\rm{H}\)\( s\)となります。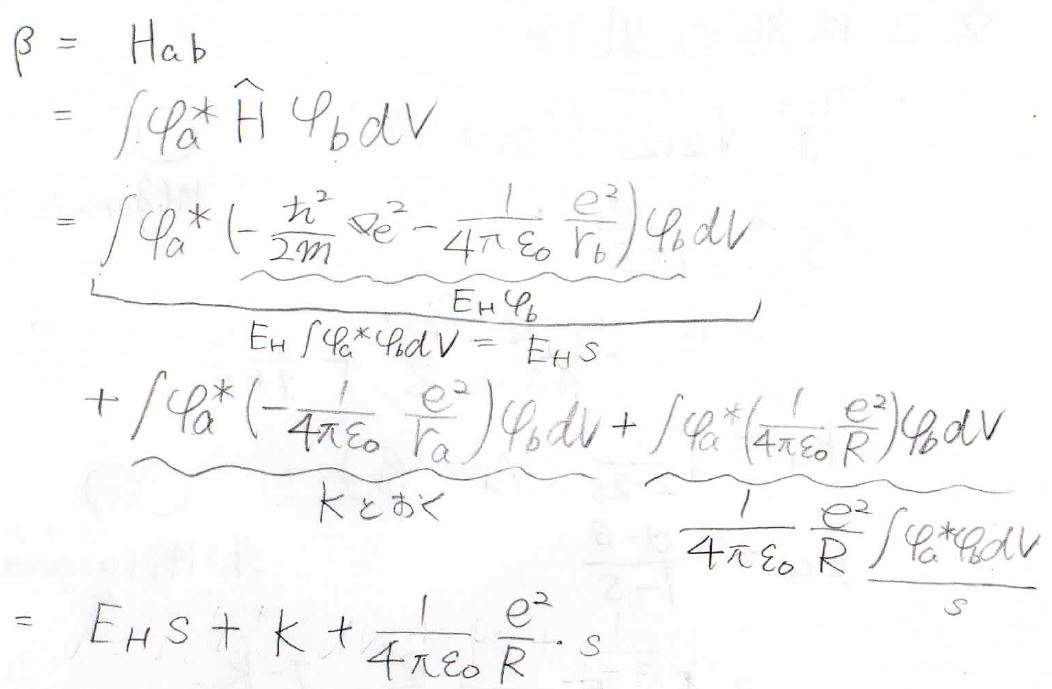
そして、第二項は\(K\)と置いておきます。
最後の第三項に関しても、プロトン間のポテンシャルを積分の前に出すと、残った積分が\(s\)になるので、\(\displaystyle \beta=E_Hs+K+\frac{1}{4\pi\varepsilon}\frac{e^2}{R}s\)となります。
\(J\)と\(K\)について
最後に、\(J\)と\(K\)について、見ていきます。
\(J\)
まず、\(J\)にはクーロン積分という名前がついています。
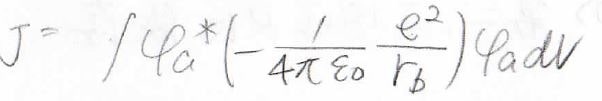
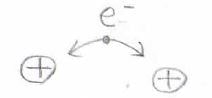
波動関数は\(\rm{a}\)のプロトンについてですが、ポテンシャルは\(\rm{b}\)のプロトンについてということなので、絵で描くと下のようなイメージです。
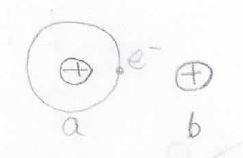
\(\rm{a}\)のプロトンが電子を束縛して、水素原子として存在しているところの近くに\(\rm{b}\)プロトンを置いたとき、\(\rm{b}\)と電子の間で静電的な相互作用が起こります。
これによるポテンシャルの変化がクーロン積分です。
\(K\)
そして、\(K\)にも名前がついており、共鳴積分または交換積分と言います。
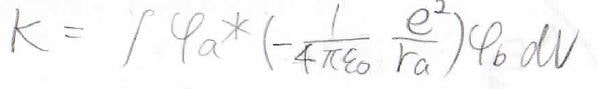
これは、2つの原子核が1個の電子を共有することで生じるエネルギーの安定化を表します。
金属や希ガスではない水素や酸素が、原子ではなく分子の形で多く存在しているのは、電子の交換による安定化の効果が影響しています。
水素結合でも、プロトンを2つの原子で共有することによる安定化が起こっています。
一般的に、\(J\)と\(K\)は負の値となり、エネルギーの安定化を表します。
水素分子イオンの2状態の関係
最後に、水素分子イオンの2状態の関係について考えていきます。
対称な波動関数
まず、2つの原子軌道を足したものから考えます。
この状態では同じ位相で、1対1の寄与があるので、このように対称な形になっています。

これをドイツ語でgerade(ゲラーデ)と言い、\(\rm{g}\)を添え字につけて表します。
非対称な波動関数
もう1つの状態は、このように非対称な形になっていてungerade(ウンゲラーデ)と言います。
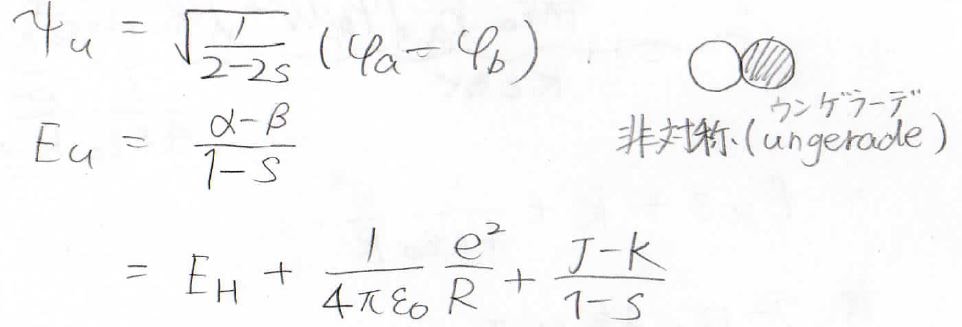
添え字として、\(\rm{u}\)をつけて表します。
\(E_\rm{g}\)と\(E_\rm{u}\)を見比べると、第一項と第二項は共通していて、第三項だけが違うものになっています。
そして、第一項は水素原子のエネルギーであるため定数ですが、第二項と第三項は\(R\)についての関数になります。
それぞれのポテンシャル
以上のことより、\(E_\rm{H}\)を基準として、\(R\)に対してのそれぞれのエネルギーを考えると、下のようになります。
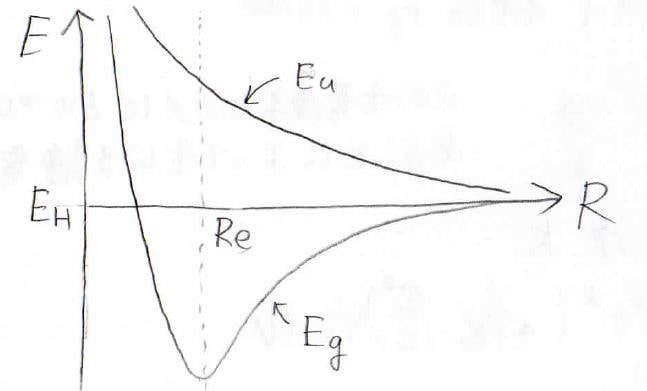
常に\(E_\rm{H}\)より高いエネルギーになっているものが非対称な\(E_\rm{u}\)で、ある程度の距離から安定化が起こっているほうが対称な\(E_\rm{g}\)になります。
\(E_\rm{g}\)に関しては、摂動法の例で考えた非調和な振動子の形になっています。
詳しくはこちらをご覧ください。

\(\displaystyle E_\rm{g}\)の最小値を与える距離を\(R_\rm{e}\)として、そのときの両者のエネルギーを考えると、下のようになります。
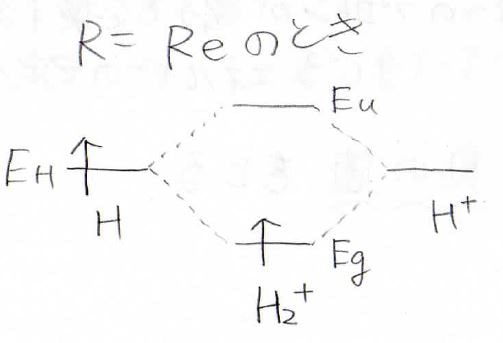
左が水素原子、右がプロトンの空軌道で、それらを合体させてできる水素分子イオンの軌道が真ん中にあります。
2つの軌道からは新しい軌道がまた2つできて、元のエネルギーより安定なものと不安定なものができます。
1個の電子についてだけ見ると、エネルギーは下がっているので、水素分子イオンは水素原子より安定であると言えます。
このように、複数の核で電子を共有して安定な軌道が作れるということこそが共有結合の原理となります。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!