こんにちは！
それでは今回も化学のお話やっていきます。
今日のテーマはこちら！
動画はこちら↓
動画で使ったシートはこちら(critical point)
「臨界点」という言葉自体は、高校でも習いますが、大学の知識を使って、考えてみましょう。
それでは、内容に入っていきます！
ファンデルワールスの状態方程式と臨界点
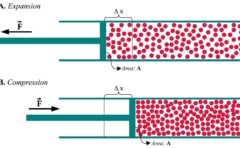
それでは初めに、実在気体のモデルとなるファンデルワールスの状態方程式について、復習をします。
下の式が、ファンデルワールスの状態方程式で、分子がもつ大きさと分子間力の効果を考えた形になっています。
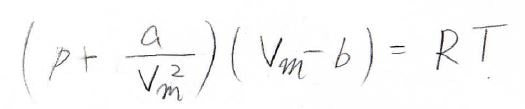
理想気体では、ボイルの法則より、圧力はモル体積に反比例し、単調減少していきますが、この式は圧力が変曲点を持ちうる形になっています。
変曲点を持つかどうかは温度に依存しまして、↓の図がその温度変化を表したものになります。
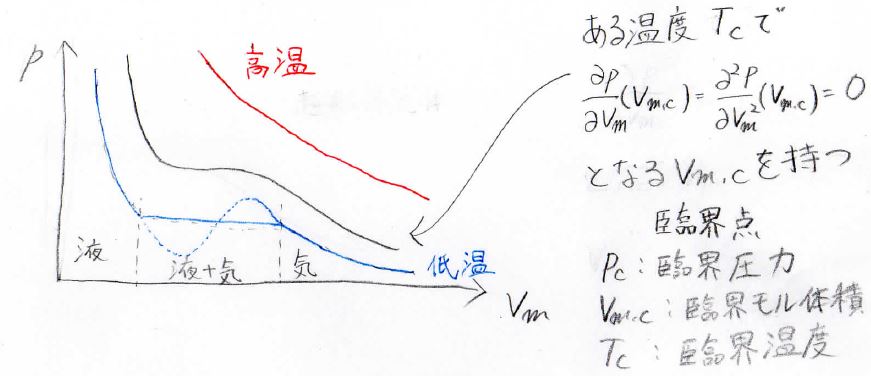
青が低温、赤が高温です。
高温では、ボイルの法則に近い形になりますが、低温では、体積の増大に伴って圧力が増大するという非現実的な現象を予想する形になってしまいます。
実際にこのようなことは起こらないので、水平線による置き換え(マクスウェルの規則、当面積則)をして考えます。
すると、この水平線の領域では圧力が体積に依存しないということから、液体と気体の共存状態であると考えることができます。
この巣閉栓の高さに当たる圧力こそが、飽和蒸気圧ということです。
その場合、この共存領域よりもモル体積が小さい領域が液体のみ、モル体積が大きい領域は気体のみが存在しているということになります。
高温では、変曲点がなくなることからも予想されるとおり、温度が高いほど、この気液共存領域は狭くなっていきまして、ある温度では一階と二階の偏導関数が\(0\)となるような、モル体積の値を持つようになります。
それが、上図の黒い線にあたりまして、この温度より高温では、液体と気体の共存領域がなくなる、もっと言うと液体と気体が区別できなくなります
ちょうどその境目のことを臨界点と呼びまして、その時の圧力、モル体積、温度はそれぞれ臨界圧力、臨界モル体積、臨界温度と呼び、臨界を表すcriticalのcを付けることが多いです。
また、これらは臨界定数と呼ばれまして、物質に固有の値になります。
\(p\)-\(T\)グラフにおける臨界点
\(p\)-\(T\)グラフで見た時には、固相、液相、気相の相境界がある中で、ちょうど、気液相境界がなくなる点が臨界点になります。
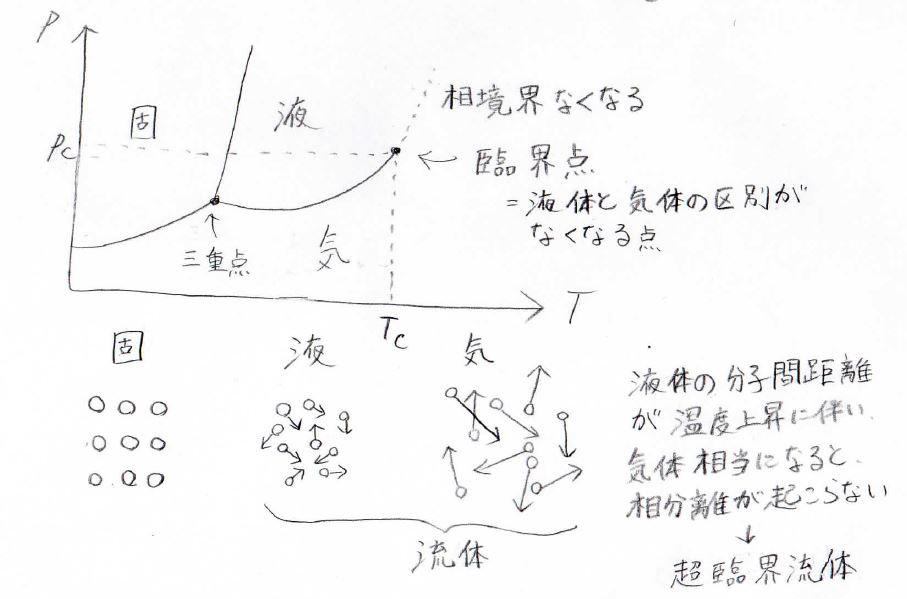
そもそも液体と気体は、共通して分子の配列がランダムであり、流れるという性質を持っているので、どちらも流体という分類に属します。
液体と気体が区別できているのは、分子間距離に明確な違いがあるからですが、温度が上がると、液体の分子間距離がどんどん大きくなっていきます。
それが気体と同じくらいになったところで、両者の違いがなくなり、超臨界流体と呼ばれる状態になります。
気体のような拡散性と、液体のような溶解性を併せ持つという性質があり、代表的な例としては、抽出やクロマトグラフィーに利用されています。
臨界定数を求める
それでは、ここからはファンデルワールスの状態方程式を使って臨界定数を求めてみます。
臨界温度における\(p\)-\(V_m\)カーブで、一階と二階の偏導関数が\(0\)になるモル体積が、臨界モル体積になります。
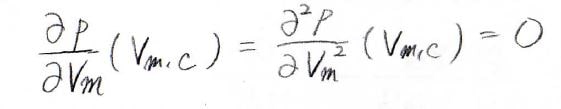
ファンデルワールスの状態方程式を\(p\)について整理すると、下の形になります。
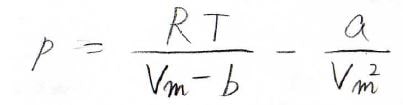
これを偏微分すると、下のようになります
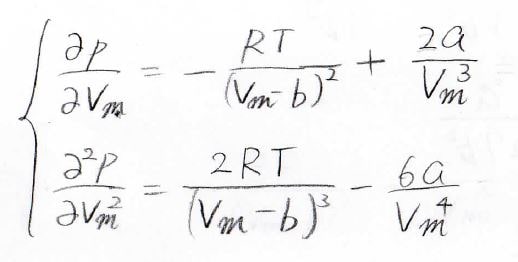
これらが、ある温度、モル体積でどちらも\(0\)になるので、このような連立方程式を立てることができます。
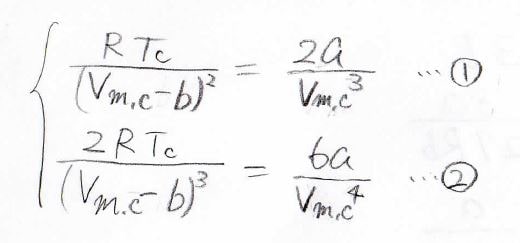
上の式を①、下の式を②として、①式を②式で割ると、\(T_\rm{c}\)\(\)が消去できて、\(V_\rm{m, c}\)\(=3b\)と出てきます。
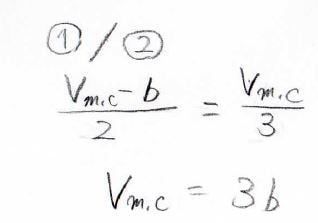
これを①式に代入すると、\(T_\rm{c}\)\(\)は\(8a/27Rb\)と計算できます。
最後に、ファンデルワールスの状態方程式に\(T_\rm{c}\)\(\)と\(V_\rm{m, c}\)\(\)を代入することで、\(p_\rm{c}\)\(=a/27b^2\)となります。
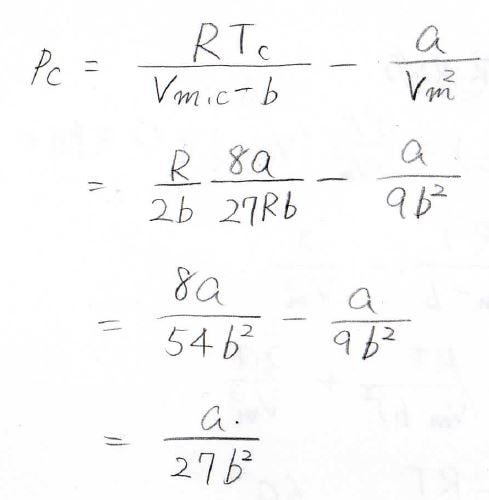
まとめると、\(V_\rm{m, c}\)\(=3b\)、\(T_\rm{c}\)\(=8a/27Rb\)、\(p_\rm{c}\)\(=a/27b^2\)であり、物質定数の\(a\)と\(b\)から求められるため、確かにこれらも物質定数になります。
まとめ
はい、それでは最後軽くおさらいをやって終わります。
今は臨界点についてお話ししました。
ファンデルワールスの状態方程式は、低い温度で\(p\)-\(V_\rm{m}\)\(\)グラフが変曲点を持つ形になっているのですが、実際には、それは非現実的なので、巣閉栓に置き換えて、気体と液体が共存している状態と見ます。
そして、ちょうど変曲点がなくなるところを臨界点と呼びます。
臨界点における温度、圧力、モル体積は物質に固有で、臨界定数と呼ばれます。
液体と気体は分子間距離に明確な違いがありますが、分子の配列がランダムであるという共通点があり、流体という同じ分類に分けられます。
温度の上昇と伴い、液体と気体の分子間距離が同じになったところが臨界点であるため、その物理的な意味は、ちょうど液体と気体が区別できなくなる点ということになります。
臨界温度以上では、液体とも気体とも言えない、超臨界流体という状態になります。
ここでは、液体と気体の性質を併せ持つような性質を示し、抽出やクロマトグラフィーへ利用されています。
そして、ファンデルワールスの状態方程式から臨界定数は求めることができ、\(V_\rm{m, c}\)\(=3b\)、\(T_\rm{c}\)\(=8a/27Rb\)、\(p_\rm{c}\)\(=a/27b^2\)ということになります。
それではどうもありがとうございました！
