こんにちは!
それでは今回も化学のお話やっていきます。
今回のテーマは、こちら!
動画はこちら↓

動画で使ったシートはこちら(reversed Carnot cycle)
それでは、内容に入っていきます!
「逆」の意味
それではまず、逆カルノーサイクルの「逆」の意味から、始めていきます。
まず、こちらはカルノーサイクルで、2つの等温変化と2つの断熱変化で構成されています。
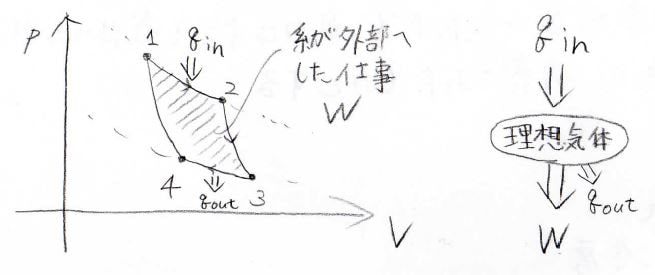
\(p\)-\(V\)グラフ上で時計回りになるように変化させることで、熱を仕事に変換させる装置ができます。
具体的に熱を受け取るのは等温膨張過程で、系が外部へした仕事がこのサイクルによって閉じられた部分の面積に相当します。
また、受け取った熱のうちの一部は、必ず等温圧縮過程で熱のまま放出されます。
そして、逆カルノーサイクルの模式図は、下のような形です。
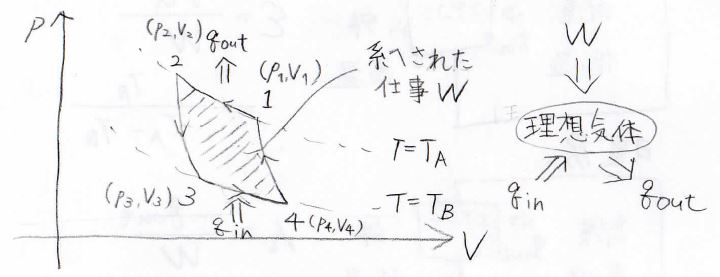
2つの等温変化と2つの断熱変化で1周するのは同じですが、変化する方向が逆の反時計回りになります。
このように変化させると、閉じられた領域の面積は、系へされた仕事に等しくなります。
また、熱を受け取る等温膨張過程が低温熱源、熱を放出する等温圧縮過程が高温熱源で起こるようになります。
逆カルノーサイクルの役割を表したものが右上の図で、系へ仕事を与えることにより、熱を低温側から高温側へと送っているということになります。
何も仕事をしていないとき、熱は高温側から低温側へと流れていくのが普通なので、系に対して仕事をするというのが、逆カルノーサイクルのポイントになります。

各過程における仕事と熱
これ以降の話では各過程における熱と仕事を考えていきますが、定積熱容量\(C_V\)の温度依存性は無視できるものとします。
また、系は可逆系であることを仮定します。
それでは、各過程を個々に考えていきます。
等温圧縮(\(1\)→\(2\))
まずは状態\(1\)から\(2\)への等温圧縮過程です。
カルノーサイクルの記事で、すでにやったことなので、さわりだけお話ししていきます。
詳しくは、こちらを参考にしてください。

変化が始まってから終わるまでのトータルの量は、微小量の積分によって得られます。
系に与えられた微小な仕事\(\rm{d’}\)\(w\)は\(-p\rm{d}\)\(V\)となり、理想気体の状態方程式より\(\displaystyle p=\frac{nRT}{V}\)となるため、トータルの仕事\(w\)は\(-nRT_\rm{A}\)\(\displaystyle \ln{(\frac{V_2}{V_1}})\)となります。
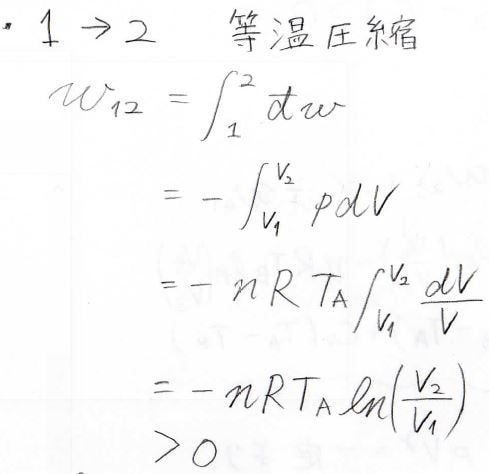
理想気体の内部エネルギーの変化量は温度の変化量に比例するため、等温変化では内部エネルギー一定ということになります。
したがって、熱力学第一法則より系へ与えられた熱量\(q\)は\(-w\)となります。

\(V_2\)は\(V_1\)より小さいため、この\(q\)の値は負であり、実際には熱が放出されていることになります。
断熱膨張(\(2\)→\(3\))
続いて、状態\(2\)から\(3\)への断熱膨張過程です。
熱の出入りがないとき、系へ与えられた熱量は、内部エネルギーの変化量に等しくなるため\(C_\rm{V}\)に温度の変化量をかけた値となります。

\(T_\rm{A}\)は\(T_\rm{B}\)より高いため、これは負の値になります。
等温膨張(\(3\)→\(4\))
そして、状態\(3\)から\(4\)への等温膨張過程でも、先ほどと同様にして求めることができます。

\(V_4\)は\(V_3\)よりも大きいため、\(q\)は正の値となり、ここで熱を受け取っていることになります。
断熱膨張(\(4\)→\(1\))
最後、状態\(4\)から\(1\)でも仕事がこのように導かれ、この値は正になります。

サイクル全体
サイクル全体で、系に与えられた仕事を考えると、断熱過程の値がキャンセルして、等温過程の値だけが残ります。

また、ポアソンの式を使うと、\(\displaystyle \frac{V_4}{V_3}\)が\(\displaystyle \frac{V_1}{V_2}\)と等しいことがわかるので、これを代入すると、サイクル全体の仕事\(W=nR(T_\rm{A}\)\(-T_\rm{B}\)\(\displaystyle )\ln{(\frac{V_1}{V_2})}\)となります。
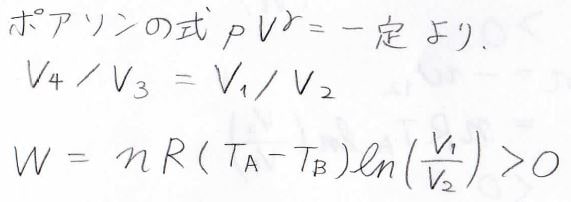
ポアソンの式の導出過程については、こちらを参照してください。
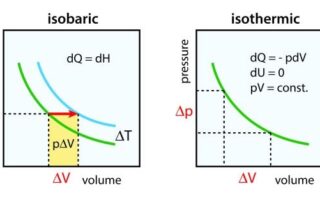
この値は、\(p\)-\(V\)グラフ上において、サイクルによって閉じられた領域の面積に等しくなります。
逆カルノーサイクルの効率
実は、逆カルノーサイクルの効率は2通り考えることができます。
冷却効率
まずは、熱を奪う装置としての効率、すなわち冷却効率です。
\(\varepsilon\)として表すと、これは、系にした仕事に対して受け取った熱の量と定義され、結局\(\displaystyle \frac{T_\rm{B}}{\mathit{T}_A-\mathit{T}_B}\)と、温度だけで表される値になります。

ヒートポンプの効率
そして、逆カルノーサイクルは熱を送る装置、すなわちヒートポンプとしてもとらえることができます。
その効率を\(h\)とすると、これは、系にした仕事に対して、放出された熱の量として定義されます。
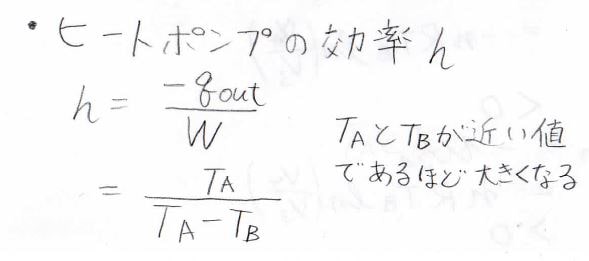
これも結局\(\displaystyle \frac{T_\rm{A}}{\mathit{T}_A-\mathit{T}_B}\)と、温度だけで表される値になります。
練習問題
それでは最後に、練習問題をやってみましょう。
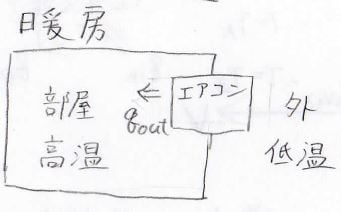
理想的な逆カルノーサイクルをエアコンとして利用することを考えます。
消費電力が同じとしたとき、暖房と冷房でどちらのほうが効率が良いと言えるでしょうか?
ただし、エアコンの形はまったく同じで、電力のすべては気体への仕事のために消費されたものとします。
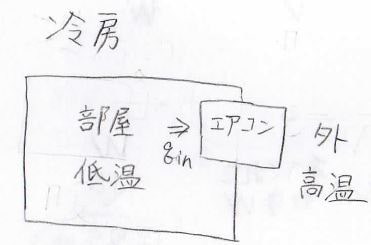
外にどれだけの熱が放出されるかは、部屋の中の人からすれば問題ではないわけです。
このときの効率は、エアコンに与えられる熱量\(q_\rm{in}\)が分子側となるため、\(\displaystyle \frac{T_\rm{B}}{\mathit{T}_A-\mathit{T}_B}\)と書けます。
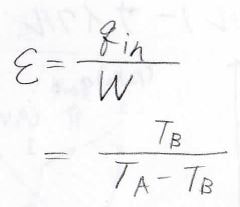
暖房のときには、逆にエアコンから出てくる熱のほうが部屋の中の人から見て重要になります。
したがって熱効率は、エアコンから放出される熱量\(q_\rm{out}\)が分子側となり、\(\displaystyle \frac{T_\rm{A}}{\mathit{T}_A-\mathit{T}_B}\)と書けます。
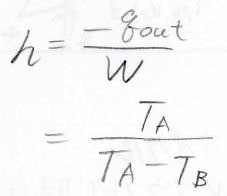
\(T_\rm{A}\)は\(T_\rm{B}\)より高い温度であるので、\(h\)は必ず\(\varepsilon\)より大きくなります。

したがって、暖房の方が効率が良いということになります。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!