こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(Joule-Thomson)
それでは内容に入っていきます!
ジュール-トムソン係数
まず前提として、この動画ではエンタルピーは温度\(T\)と圧力\(p\)の二変数関数であるとします。
理想気体であれば、温度\(T\)だけでよいので、ここではより一般的な系を考えています。
ファンデルワールスの状態方程式からもわかるように、一般的な系では2つの状態量によってその他の状態量が決まります。
ファンデルワールスの状態方程式については、こちらをご参照ください。

そして、エンタルピーの全微分\(\rm{d}\)\(H\)は、下のように書けます。
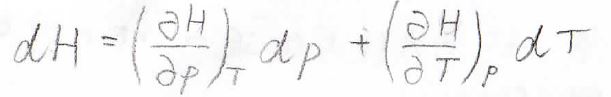
\(\displaystyle (\frac{\partial H}{\partial T})_p\)は定圧熱容量\(C_p\)と書き換えられます。
また、前回も使ったオイラーの連鎖式を使うと、\(\displaystyle (\frac{\partial H}{\partial p})_T=-(\frac{\partial H}{\partial T})_p(\frac{\partial T}{\partial p})_H\)となります。
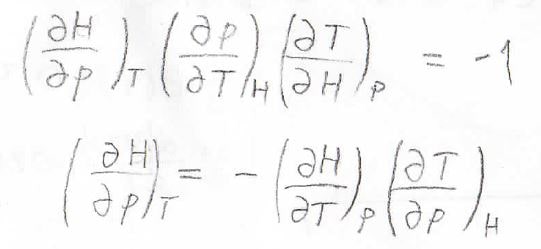
したがって、定圧熱容量\(C_p\)のほかに、\(\displaystyle (\frac{\partial T}{\partial p})_H\)というパラメータ、すなわちエンタルピー一定で圧力を変化させたときに温度がどう変化するかというのが必要になってきます。

この量は、ジュール-トムソン係数と呼ばれているもので、ここでは\(\mu\)と表すことにします。
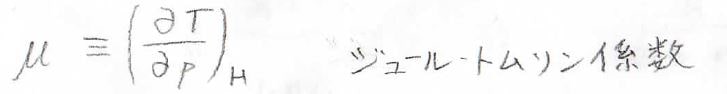
等エンタルピー変化
次に、エンタルピー一定条件での変化は、どのようなものかを考えていきましょう。
圧力一定条件では、系へ与えられた熱量がエンタルピーの変化量に等しいことを利用します。
実際にその一例を示したのが、こちらの図です。

右からも左からも押せるようにピストンがついた容器を使います。
壁面はすべて断熱されていて、容器の中には左右の空間を隔てるように多孔質膜がついています。
この容器の中に、気体を入れて、右のピストンが隔膜に接した状態、これを変化前とします。
このときの圧力、体積、温度をそれぞれ\(p_\rm{i}\)、\(V_\rm{i}\)、\(T_\rm{i}\)とします。
そして、ここから左のピストンがゆっくり右へ動いていって、すべての気体が右の空間へ移動した状態を変化後とします。
このときの圧力、体積、温度をそれぞれ\(p_\rm{f}\)、\(V_\rm{f}\)、\(T_\rm{f}\)とします。
\(p_\rm{f}\)は\(p_\rm{i}\)より低い圧力です。
これで本当にエンタルピー一定になっているかどうかは、次のように確かめられます。
考え方としては、まず隔膜の左側だけに着目します。

すると、圧力が\(p_\rm{i}\)で一定のまま、体積が小さくなっています。

体積が\(0\)になったとき、系がされた仕事は\(p_\rm{i}\)\(V_\rm{i}\)になります。
熱の出入りはないため、この仕事が内部エネルギーの変化量となります。
同様に、隔膜の右側について考えると、気体は体積\(0\)から\(V_\rm{f}\)まで定圧膨張しているため、系がされた仕事は\(-p_\rm{f}\)\(V_\rm{f}\)となります。
したがって、全体で系がされた仕事は\(p_\rm{i}\)\(V_\rm{i}\)\(-p_\rm{f}\)\(V_\rm{f}\)であり、これが内部エネルギーの変化量になります。
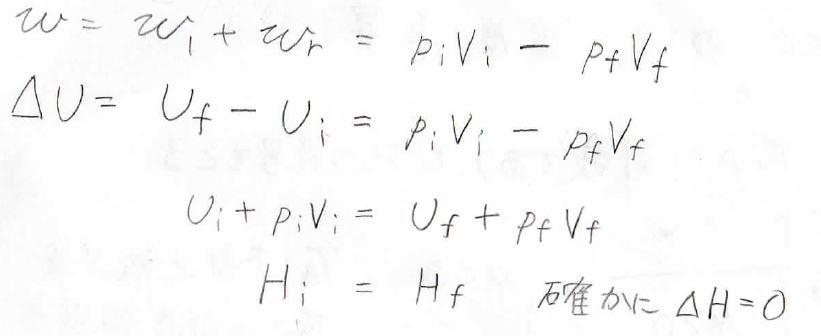
変化前の内部エネルギーを\(U_\rm{i}\)、変化後の内部エネルギーを\(U_\rm{f}\)として整理すると、結局\(U+pV\)、すなわちエンタルピー\(H\)が一定となることがわかります。
ジュール-トムソン係数の実験的決定方法
実験的にジュール-トムソン係数を決めるときには、上記のような装置を使って、圧力が変化する前後の温度変化を観測します。
圧力差\(\Delta p\)をどんどん小さくしていくことで、微分量を推定することができます。
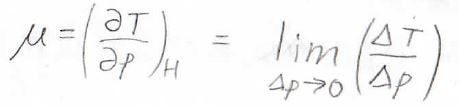
ただし、完璧に近い断熱系を実際に作るのは困難であるため、実験的には別の方法をとったほうが精度よく調べることができます。
その方法を図で表したのがこちらです。
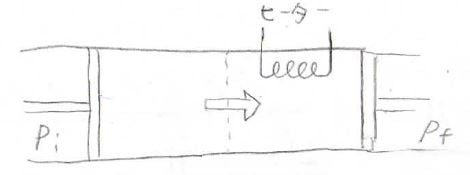
ここでは、断熱ではなく温度一定としています。
圧力を小さくして膨張させると温度が変化するので、そこにヒーターで熱を与えて温度を一定とします。
オイラーの連鎖式を使うと、ジュール-トムソン係数\(\displaystyle \mu=-\frac{1}{C_p}(\frac{\partial H}{\partial p})_T\)と書けます。
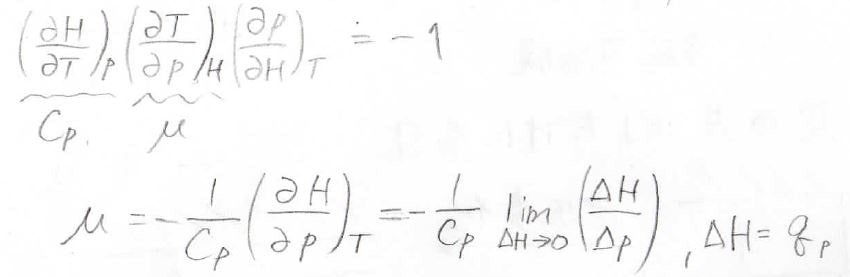
エンタルピーの微小変化量\(\Delta H\)は定圧条件下で系に与えられた熱量\(q_p\)に等しいため、ヒーターの電力から簡単に求められます。
この\(\displaystyle (\frac{\partial H}{\partial p})_T\)は、等温ジュール-トムソン係数と呼ばれており、実験的にはこの値を測定し、間接的にジュール-トムソン係数を求めることになります。
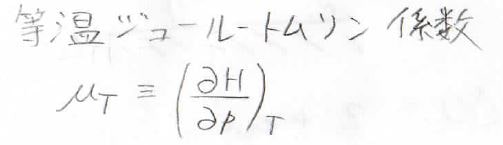
ジュール-トムソン効果の分子論的解釈
ジュール-トムソン効果の分子論的な説明は、次のとおりです。
まず、気体分子の熱運動エネルギーは温度に比例するため、分子の運動が速いということは温度が高いことと同じであるということを理解した前提で進めていきます。

冒頭でもお話したとおり、理想気体では等エンタルピー膨張による温度変化は起こらないため、重要になるのは分子間相互作用です。
仮に分子間引力が優勢であった場合、分子間距離が小さいほど安定、すなわちポテンシャルエネルギーは小さくなります。
したがって、膨張したときにはポテンシャルエネルギーは増大します。
このとき、気体がもつ全エネルギーに変化がないとすると、ポテンシャルエネルギーが大きくなった分だけ運動エネルギーが小さくなることになります。
運動エネルギーが小さくなることは温度が低くなることと同義であるため、温度の低下が観測されることになります。
このとき、ジュール-トムソン係数\(\mu\)の符号は正になります。

反対に、分子間で反発力が優勢な場合は、等エンタルピー膨張により温度は上昇します。
このとき、\(\mu\)の符号は負になります。
ジュール-トムソン係数の温度、圧力依存性
分子間で引力と反発力のどちらが優勢なのかは、もちろん気体の種類によって違いますが、同じ気体であっても温度や圧力に依存します。
実際に、\(\mu\)の符号は下のグラフのように変化します。

境界線上の点では\(\mu=0\)、斜線を書いている領域が\(\mu>0\)、書いていない領域が\(\mu<0\)です。
一般的に、ある圧力未満で符号の入れ替わりが2回起きることが知られており、入れ替わりが起きる低温側の温度を下部逆転温度、高温側の温度を上部逆転温度と呼びます。
リンデの冷却機
最後にこのジュール-トムソン効果を利用して、ヘリウムなどの低温液体を作る方法を見てみましょう。
有機実験で、溶媒の温度を沸点にするときにに還流を行いますが、これも還流の話です。
下がそのイメージ図で、コンプレッサーで圧力差をつくっておき、膨張とともに冷却が起こるようにしておきます。
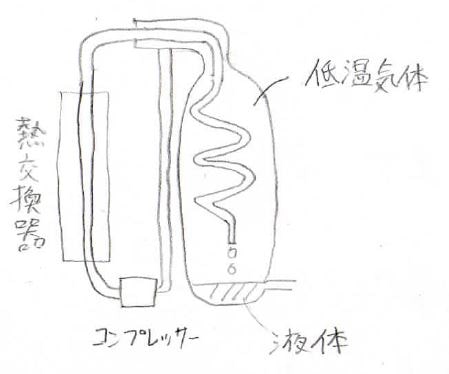
すると、容器の中が低温の気体で満たされることになります。
この気体は高圧側の気体を冷却するので、新しく入ってきた気体は二重で冷却されることになります。
これを繰り返していくと、どんどん温度は低下していき、あるところで液体になるという仕組みです。
この装置は、リンデの冷却機と呼ばれています。
ここで疑問なのが、低温になることで理想気体に近づくと、ジュール-トムソン係数も\(0\)に近づいていき、冷却が起こらなくなるのではないかということです。
しかし、これは間違いで冷却は起こり続けます。
それは、ジュール-トムソン係数が温度や圧力に直接依存しているわけではなく、それらの導関数によって決まるということを意味しています。
言葉で言ってもわかりにくいので、第2ビリアル係数とほとんど同じだと考えてください。
ビリアル状態方程式については、こちらをご参照ください。


低温に近づくと、この値は確かに\(0\)に近づくため、理想気体の状態方程式は成り立つようになります。
しかし、その温度についての微分はといえば、ボイル温度で\(0\)、それより低温で負、高温で正になります。
理想気体の状態方程式が成り立ったとしても、その導関数まで理想気体の予想に一致するとは限らないので注意してください。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




