こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(mobility)
それでは内容に入っていきます!
液体と気体の違い
まず、前回お話しした気体と今回お話しする液体で決定的に違うことは、分子間距離です。
気体を理想気体として考えていたのでなおさらですが、液体では分子間相互作用を無視することができません。
液体中で1つの分子が動くためには、周囲の分子との相互作用をいったん断ち切って新たに安定な状態を作る必要があります。

分子がボルツマン分布に従うときには、粘性率は分子の動きにくさのパラメータであるため、\(\displaystyle \exp{(\frac{E_\rm{a}}{\mathit{RT}})}\)に比例すると予想されます。
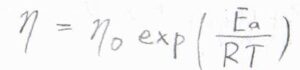
ここで\(E_\rm{a}\)がモルあたりのエネルギー障壁の高さ、\(R\)が気体定数、\(T\)が絶対温度です。
定数である\(\eta_0\)は粘性率の高温極限です。
気体の粘性率は、絶対温度の平方根に比例するので、温度に対して単調増加となりますが、液体の場合は単調減少の関数になります。

ただし、この予想はあくまで体積が一定だった場合のものであり、実際には温度に伴い密度が変化し、分子間距離が変化したことによりエネルギー障壁の高さ\(E_\rm{a}\)も変化するため、もっと複雑な温度依存性を示すのが一般的です。
また、温度が低いときの水では、圧力が増加するにつれて粘性率が減少するということが知られています。
対して、多くの液体では、圧力増加で\(0.1\sim 0.3\%\)程度の粘性率増大が起こります。
水に特徴的なこの挙動は、水分子が移動するために水素結合を切断する必要があることによる影響と考えられています。
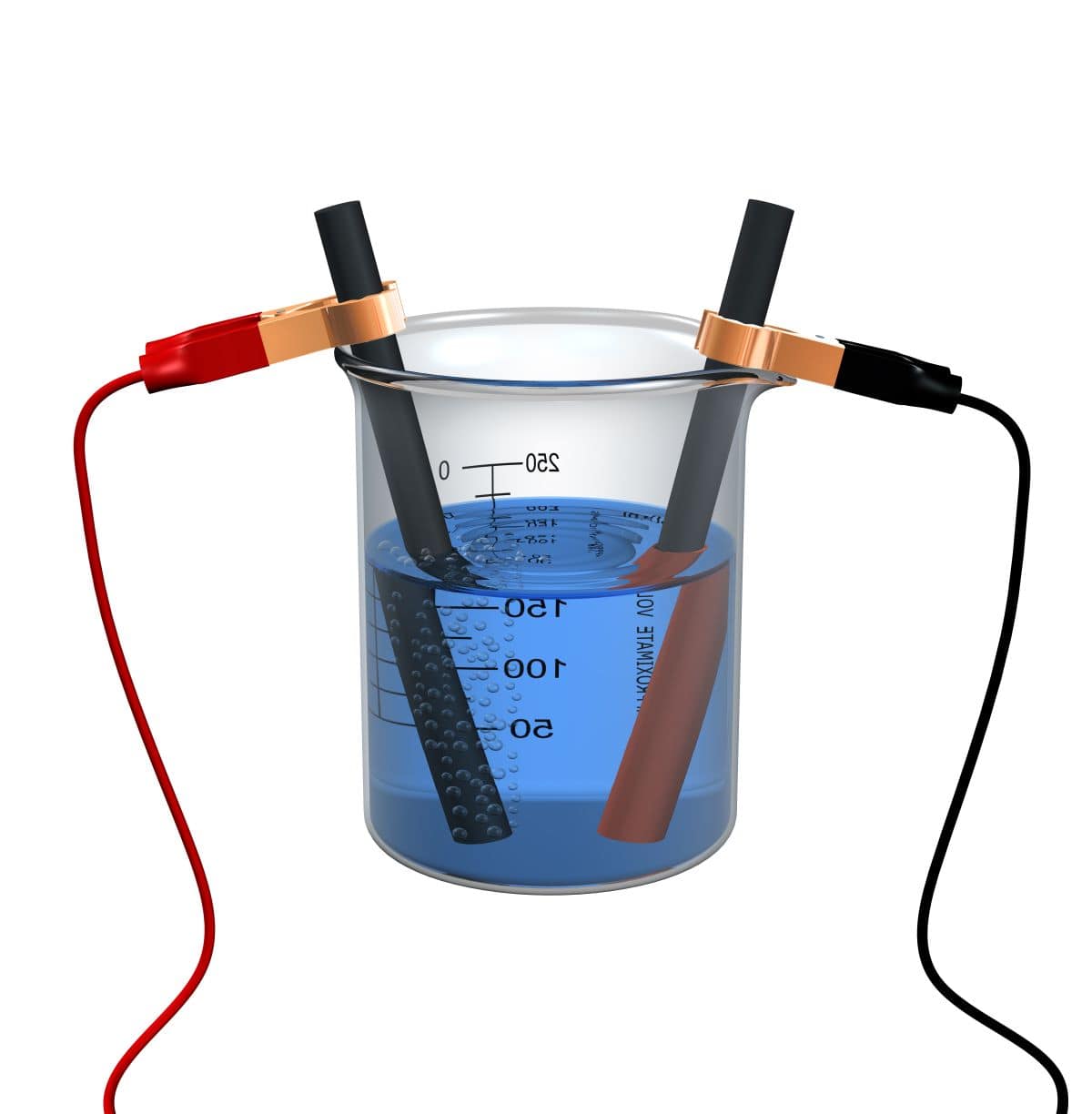
電気伝導率
ここからは、電解質溶液中におけるイオンの動きやすさや電気伝導率を考えていきます。
なぜ先にイオンから考えるかというと、イオンにはたらく力の大きさとイオンの速さをいったん求めてから、電場を消去することで電気的に中性な分子やコロイドの動きも考えるという順序で式の導出を行うためです。
詳しくは、こちらを参照してください。
まず、容器を電解質溶液で満たし、そこに電圧を印加した状態を考えます。
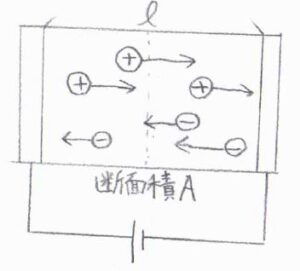
電極間の距離を\(l\)、容器の断面積を\(A\)とします。
溶液中のイオンは電荷の符号により、いずれかの電極側へ力を受ける状態です。
この系において、コンダクタンス\(G\)というものを考えます。
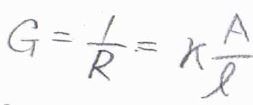
これは電気抵抗の逆数で、単位は\(\Omega^{-1}\)です。
かつてこの単位をモーと呼んだそうですが、現在は\(\rm{S}\)と書いてジーメンスと呼ぶのが一般的です。
電気抵抗は、抵抗器の長さに比例し、断面積に反比例するため、コンダクタンスは断面積\(A\)に比例し、長さ\(l\)に反比例します。
そして、その比例定数である\(\kappa\)を電気伝導率と言います。
電気伝導率は、存在するイオンの個数に依存するため、一般的にはモル濃度で割ったモル伝導率\(\Lambda_\rm{m}\)として考えます。
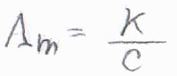
典型的な値として、\(\Lambda_\rm{m}\)は\(10\ \rm{mS\ m^2\ mol}\)\(^{-1}\)程度となります。
単純には、モル伝導率は濃度に依存しないように思えますが、実際は遮蔽や溶媒和の影響で、名目上の濃度と活量に比例関係が成立しないことがほとんどであるため、モル伝導率には濃度依存性があります。
濃度の低い強電解質においては、モル伝導率\(\Lambda_\rm{m}\)が\(\Lambda_\rm{m}\)\(\displaystyle ^\circ-Kc^\frac{1}{2}\)という濃度依存性をもつとするコールラウシュの法則が経験的に求められています。
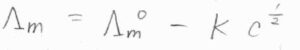
コールラウシュは、物理学者の名前です。
ここで、\(K\)は定数、\(\Lambda_\rm{m}\)\(^\circ\)は溶液を無限に希薄していったときのモル伝導率の極限で、極限モル伝導率と言います。
またコールラウシュは、極限モル伝導率がそれぞれのイオンからの寄与の総和であるとするイオンの独立移動の法則を確立しました。
イオンの極限モル伝導率を\(\lambda’\)としたとき、全体の極限モル伝導率\(\Lambda_\rm{m}^\circ\)との関係は、こちらの式のように表されます。
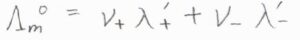
ここで、\(\nu\)は溶質である塩の化学式単位中におけるイオンの数です。
移動度(易動度)
ここからは、イオンに電圧を印加したとき、イオンにかかる力の大きさやイオンの速さを考えていきます。
まず、2つの点\(\rm{A}\)と\(\rm{B}\)は距離が\(l\)だけ離れており、電位差は\(\Delta \phi\)だったとします。

電位の大きさは\(\displaystyle \frac{\Delta \phi}{l}\)であるため、イオンにかかる力の大きさは\(\displaystyle \frac{ze\Delta \phi}{l}\)と書けます。

ここで、\(z\)はイオンの価数、\(e\)は電気素量です。
力の向きは、電位差の符号とイオンの符号によって変わりますが、今は簡単のために力の大きさだけ考えることにしています。
さらに、分子間距離が近い液体中では、イオンが移動したときに、周囲の分子からの摩擦により減速が起こります。
ここでは、速さに比例する力を考えます。

\(f\)が比例定数で、マイナスの符号は、抵抗による力が速さの向きと逆の向きにはたらくことを表しています。
イオンが半径\(a\)の球の形で、ストークスの法則が成り立つことを仮定すると、2つの力がつりあったとき、イオンの終端速さ(ドリフト速さ)\(s\)は\(\displaystyle \frac{zeE}{6\pi \eta a}\)となります。
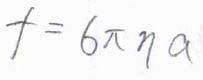
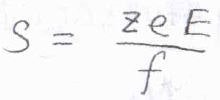
\(s\)を電位の大きさ\(E\)で除したものをイオンの動きやすさのパラメータと考えると、それは\(\displaystyle \frac{ze}{6\pi \eta a}\)と書けます。
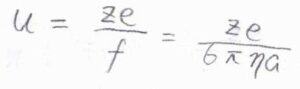
これを移動度(易動度)と呼びます。
ここでは\(u\)と表すことにします。
「いどうど」には2通りの漢字がありますが、どちらの表記を使っても構いません。
移動度は半径に反比例するので、大きなイオンほど動きにくくなります。
ただし、この式にあるイオンの半径\(a\)は、イオン自体の半径ではなく、流体力学的半径と呼ばれるものです。
流体力学的半径とは、イオンと一緒に移動する周囲の溶媒分子も含んだ有効半径のことです。
イオンの電荷が同じでも、イオン表面における電場の大きさはイオンだけの半径\(r\)の二乗に反比例することから、小さいイオンほどより多くの溶媒分子と相互作用すると言えます。
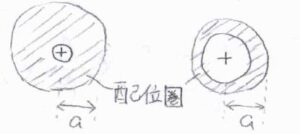
これにより、比較的小さなイオン同士では、イオン自体が大きくなるにつれて移動度が高くなることもあります。
中でも水中におけるプロトンは特別で、最も小さいイオンでありながら、とても高い移動度をもつことが知られています。
これには、結合の再配列を伴って、プロトンが実質的に長距離を移動できるグロッタス機構をはじめとして、さまざまな機構が提唱されていますが、実際のところは未だ議論中です。
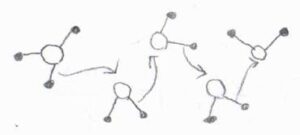
ちなみに、液体アンモニア中におけるアンモニウムイオンの移動度も高くなることが知られており、水中におけるプロトンと同様の機構であると考えられています。
イオン伝導率
最後に、イオンの移動度と電気伝導率の関係を考えて終わります。
モル濃度が\(c\)の強電解質溶液中で、カチオンとアニオンの数密度を\(\nu cN_\rm{A}\)と表します。
\(\nu\)は塩の化学式単位中におけるイオンの数で、\(N_\rm{A}\)はアボガドロ数です。
アニオンとカチオンの一方に着目したとして、イオンの流束\(J_\rm{ion}\)を考えると、\(J_\rm{ion}\)\(=s\nu c N_\rm{A}\)と書けます。
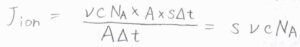
この式において、\(A\)はイオンが通過する仮想的な窓の面積、\(\Delta t\)はイオンが動いた時間です。
流束については、こちらを参照してください。

電荷の流束\(J_\rm{charge}\)は、イオンの流束と電荷\(ze\)の積なので、\(J_\rm{charge}\)\(=zs\nu cF\)と書けます。
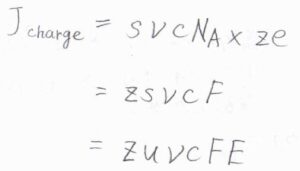
ここの\(F\)は力の大きさではなく、ファラデー定数\(N_\rm{A}\)\(e\)の意味です。
さらに、終端速さ\(s\)は、移動度\(u\)と電場の大きさ\(E\)の積であるため、\(J_\rm{charge}\)\(=zu\nu cFE\)とも書けます。
電流\(I\)は電荷の流束\(J_\rm{charge}\)と面積\(A\)の積として書けるため、\(I=zu\nu cFEA\)となります。
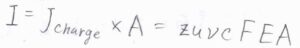
さらに、電場の大きさ\(\displaystyle E=\frac{\Delta \phi}{l}\)を代入すると、\(\displaystyle I=zu\nu cF\times \frac{A}{l}\times \Delta \phi\)となります。
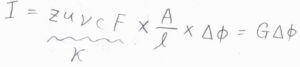
オームの法則の式と照らし合わせると、\(zu\nu cF\)が電気伝導率にあたることがわかります。
イオンのモル伝導率\(\lambda\)は、電気伝導率を濃度\(\nu c\)で割った値であるため、\(zuF\)と書けます。

これをイオン伝導率と言います。

この記事の前半でも述べたとおり、濃度\(0\)の極限においては、イオンの独立移動の法則より、全体の極限モル伝導率\(\Lambda_\rm{m}\)\(^\circ=\nu_+\lambda_++\nu_-\lambda_-\)と書けるので、\(\Lambda_\rm{m}\)\(^\circ=(z_+u_+\nu_++z_-u_-\nu_-)F\)という関係が成り立ちます。
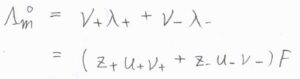
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!