こんにちは!
それでは今日も数学をやっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(cofactor-expansion)
次数が上がると、行列の成分は\(n^2\)で増えていって、置換の数は\(n!\)で増えていくので、一気に計算量が増加します。
そこで、どう対処していくのかという話をしていきます。
それでは内容に入っていきます!
行列式を変形する際のルール
まず、行列式を簡単な形へ変形させるためのルールを一気に出します。

時間がある人は、1つずつ下の定義から確かめてみてください。
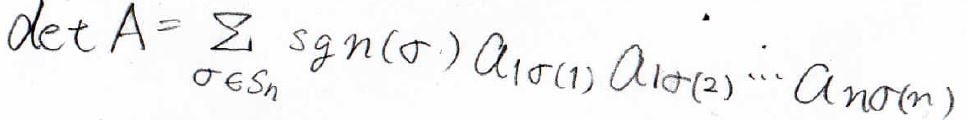
行列式の定義についてはこちらをご覧ください。

特に①、②、③が成り立てば④が成り立つというように連鎖するので、証明はそこまで難しくはありません。
4次以上の行列式の解法
では実際に、大きな行列の行列式を解いていきましょう。
なお、2次および3次の行列式の解き方については、こちらの記事で解説しています。

ここでは、便利なテクニックを2つ紹介します。
次数下げ
まず1つ目が次数下げです。
行列の\((1,1)\)成分が\(0\)ではない値で、かつ1行目または1列目の\((1,1)\)成分以外がすべて\(0\)であったとき、この行列式は下のように書くことができます。
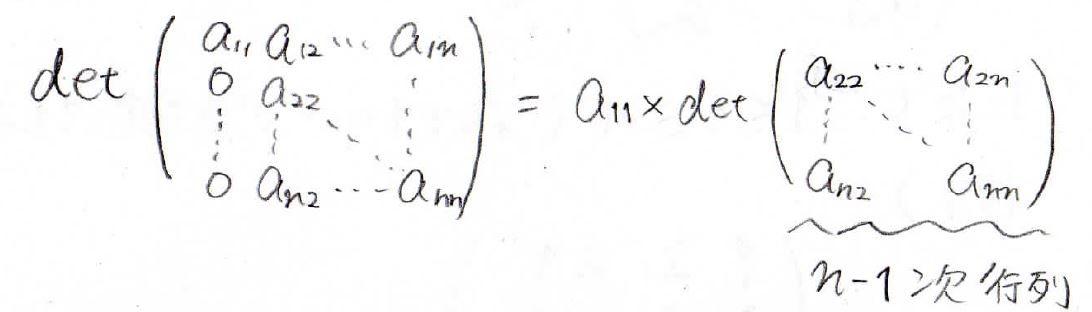
\((1,1)\)成分を前に出して、残る行列式は1行目と1列目を取り除いて次数が1つ下がったものになります。
次数が下がるほど計算が簡単になるので、この操作を繰り返して、2次や3次まで落とせば、手計算が現実的になってきます。
なぜ、次数を下げることができるのか、置換を考えてみると、\(1\)を\(1\)へ移す場合以外はすべて\(0\)になってしまうので、\(S_n\)の条件に\(\sigma (1)=1\)というのが追加されまます。
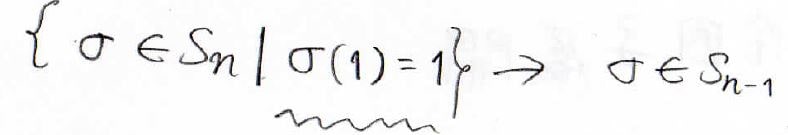
結局、\(\sigma (2)\)から\(\sigma (n)\)までを自由に変えることになるので、次数が減ることと等しくなります。
三角行列の次数下げ
この次数下げは、連続してできる場合があります。
それは、行列が三角行列や対角行列であるときで、結局、行列式は対角成分の積になります。
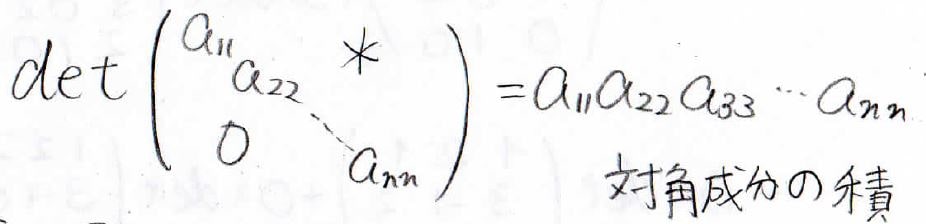
\(\ast\)の部分がどうなっていようと行列式の値は変化しません。
そのため、すべての行列式が三角行列であれば、計算は簡単にできますが、実際はそうはいきません。
そこで思い出していただきたいのが行列の簡約化です。
簡約化については、こちらの記事をご覧ください。

簡約化によって上三角行列に変形させるということをします。
ただし、簡約化した後の行列式は、元の行列式といつも同じ値になるわけではありません。
冒頭で紹介した5つのルールに則って行列式にマイナスをつけたり、定数をかけたりしながら、同時に行列の簡約化をしていくことになります。
余因子展開
では、続いて大きな行列式を解く際のテクニックの2つ目、余因子展開というものについて、お話しします。
この方法は、\(0\)が多い行または列をもつ行列について計算を行う際に、最も威力を発揮するものです。
計算式はこちらのとおりです。
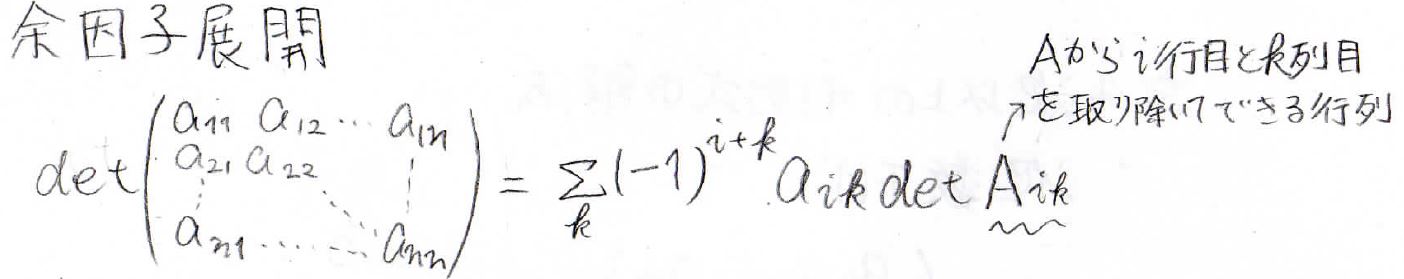
まず行列の中で着目する行または列を決めます。
ここで、着目する行はどれでもよいですが、上記の式では\(i\)行目に着目しています。
そして、今度はすべての列について考えていきます。
\(k\)列目について考えた際には、まず\((-1)^{i+k}\)に行列の\((i,k)\)成分をかけます。
最後に、元の行列から\(i\)行目と\(k\)列目を取り除いて、次数が1つ下がった行列の行列式をかけます。
実際にやってみると、次のようになります。
この行列式を2行目に着目して余因子展開していきます。
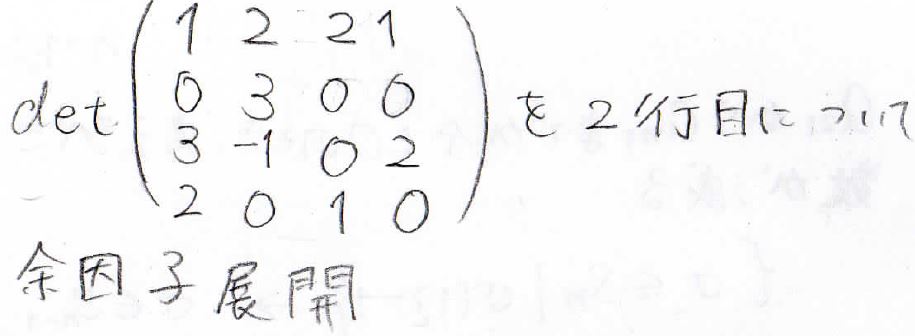
2行目を選ぶのは、成分に\(0\)が多くて計算が簡単だからです。
実際に展開するとこんな式になります。
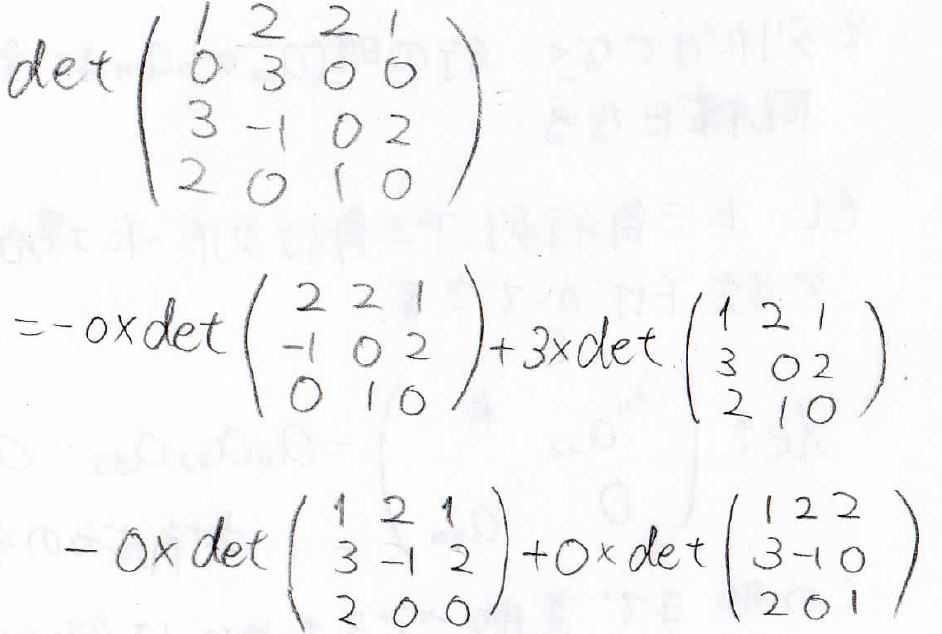
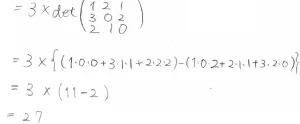
最終的には4つの項のうち3つが\(0\)になるので\(3\times 3\)次行列式という形になり、このように求めることができました。
練習問題
はい、それでは実際に練習問題をやってみましょう。
下記の行列式の値を求めてみてください。
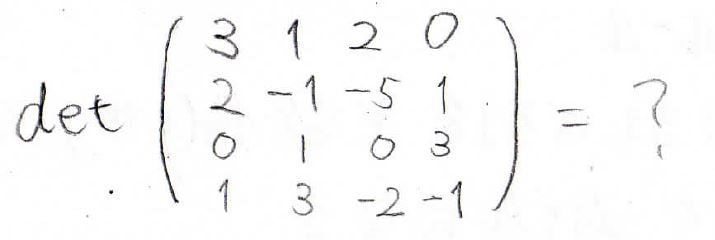
次数下げ、余因子展開どちらを使っていただいてもよいですし、両方使っても構いません。
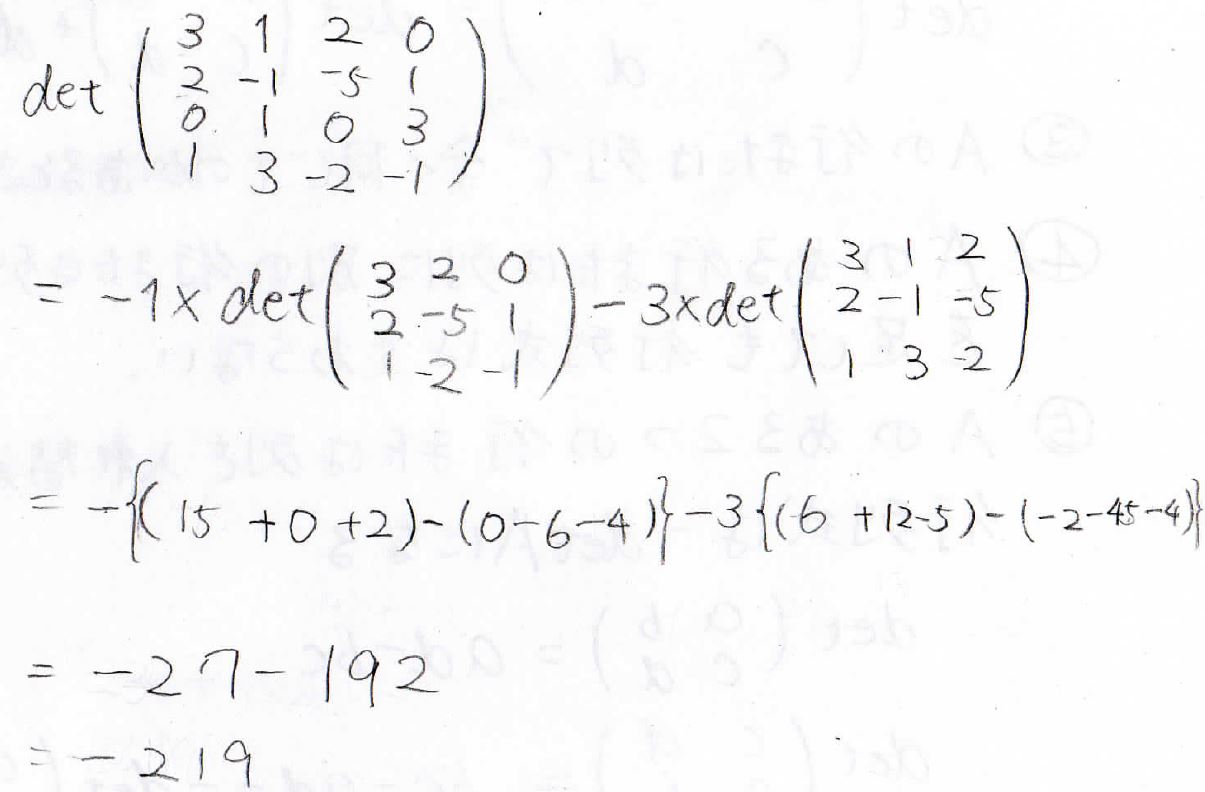
すると、最終的に\(-219\)と求められました。
次数下げでもこの値になっていれば正解です。
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




