こんにちはー!
今日は数学の話をしていきます。
今回のテーマはこちら!
行列は以前は高校で習う内容だったこともあり、化学以外にもさまざまな場面で役に立ちます。
ここでは、特に数学を専門にしない人でも使うような基本的な内容を扱いますので、行列について何も知らなくても理解いただける内容になっていると思います。
動画はこちら↓
動画で使ったシートはこちら(matrix rank)
では早速行きましょう!
行列とは
まず、行列とは?というところから入っていきます。
行列とは、例えば、下のようなものです。

\(a\)をこの行列の成分といって、\(1\)と\(0\)とか何らかの値が入ります。
そして、各成分を横に見たものを行、縦に見たものを列と呼びます。
行列の呼び方は行の数を\(n\)、列の数を\(m\)として\(n\times m\)行列と呼びます。
例えば、この行列だと\(3\times 4\)行列といいます。
そして、例えば縦のベクトル\(\boldsymbol{a}_i\)をこの行列の左から\(i\)番目の列ベクトルとして定義すると、この行列は\((\boldsymbol{a}_1, \boldsymbol{a}_2, \boldsymbol{a}_3, \boldsymbol{a}_4)\)という形で表せることになります。
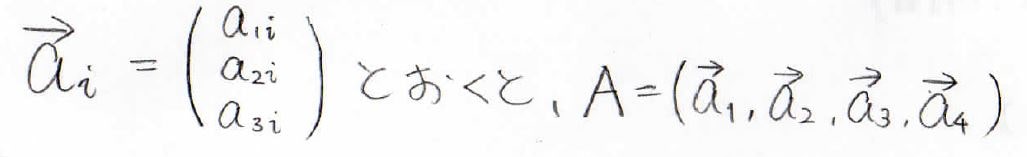
つまり、\(n\times m\)行列というのは、\(m\)個の\(n\)次列ベクトル群もしくは\(n\)個の\(m\)次行ベクトル群として考えることもできます。
特別な名前が付いている行列
そして、行列の中にはその形によって、特別な名前が与えられているものがあるので、いくつか紹介します。
まず、すべての成分が\(0\)となる行列のことを零行列と呼びます。

これはスカラーだと\(0\)、ベクトルだと零ベクトルにあたるもので、適当な行列に零行列をかけると零行列になります。
行列の演算方法については、こちらの記事をご覧ください。

そして、下の行列は\(n\times n\)行列、つまり行の数と列の数が同じ行列です。
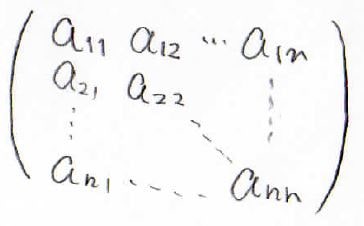
この行列を、\(\displaystyle n\)次正方行列と呼びます。
そして、正方行列の中でも対角線上の成分以外がすべて\(0\)になる場合、これを対角行列と言います。

最後は三角行列というもので、これは正方行列のうち、対角成分より下側もしくは上側の成分がすべて\(0\)になる行列です。
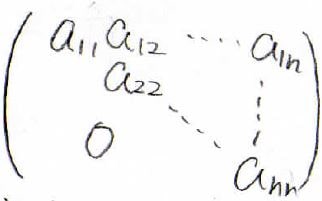
下側が\(0\)になるものは上三角行列、上側が\(0\)になるものは下三角行列と言います。
対角行列は上三角行列であり、なおかつ下三角行列でもあります。
行列の簡約化
それでは今回の動画で最も重要な簡約化という操作を説明します。
簡約化とは、行列の各行同士をスカラー倍して足したり引いたりすることで、最終的に下の形に変形させるという操作になります。
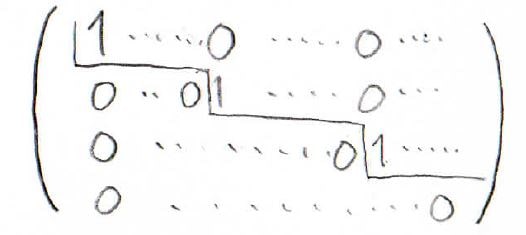
この行列では、まず各行を左から見ていったときに\(0\)ではない成分は\(1\)になるようにします。
そして、この\(1\)と同じ列の成分が\(0\)になるようにします。
続いて、左端の\(1\)が階段状になるように行を入れ替えます。
簡約化する前の行列によっては、一番下の行の成分がすべて\(0\)になることもあります。
実際にやってみたほうがわかりやすいので、試しに下の行列について、簡約化をしてみましょう。

まず、2行目の成分は\(0\)、\(2\)、\(-2\)になっていて、左端を\(1\)にしたいので\(2\)で割って\(0\)、\(1\)、\(-1\)にしておきます。
そして、1列目は\((1,1)\)成分の\(1\)以外を\(0\)にしないといけないので、この\(3\)を消すために3行目から\(3\)倍にした1行目を引きます。
続いて、2列目を\((2,2)\)成分の\(1\)以外が\(0\)になるように、1行目から2行目の\(\displaystyle 3\)倍を引いて、3行目に\(7\)倍の2行目を足します。
そうしてできた行列に最後、\((3,3)\)成分を\(1\)にして\((1,3)\)成分と\((2,3)\)成分が\(0\)になるようにすると、最終的に一番下の行列が得られました。
これは簡約化の話とは別ですが、このように成分がすべて\(1\)になる対角行列は、単位行列と呼びます。
単位行列は、スカラーでいうと\(1\)、ベクトルでいうと単位ベクトルのようなものにあたります。
何らかの行列に単位行列をかけても、かける前の行列と同じ行列になります。
行列のランク
最後、ランク(階級)という言葉も紹介しておきます。
ランクとは、その行列を簡約化したときに、すべて\(0\)にならなかった行の数です。
先ほど簡約化した行列なら、最終的に単位行列になって、\((0, 0, 0)\)という行ベクトルはなかったので、そのまま次数の\(3\)というのがランクになります。
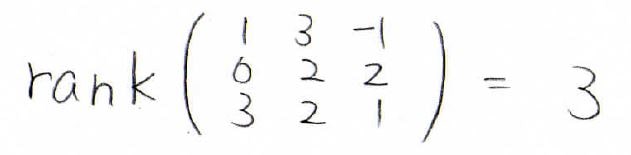
対して、例えば下のような行列の場合は、3行あるうちの一番下だけがすべて\(0\)になっているので、ランクは1つ減って\(2\)となります。

練習問題
それでは最後に、練習問題をやってみましょう。
下記の行列のランクは、いくらになるでしょうか?
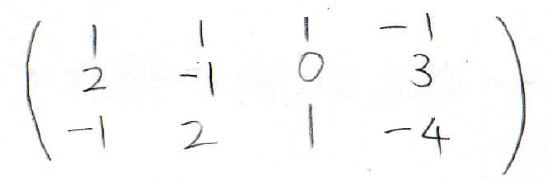
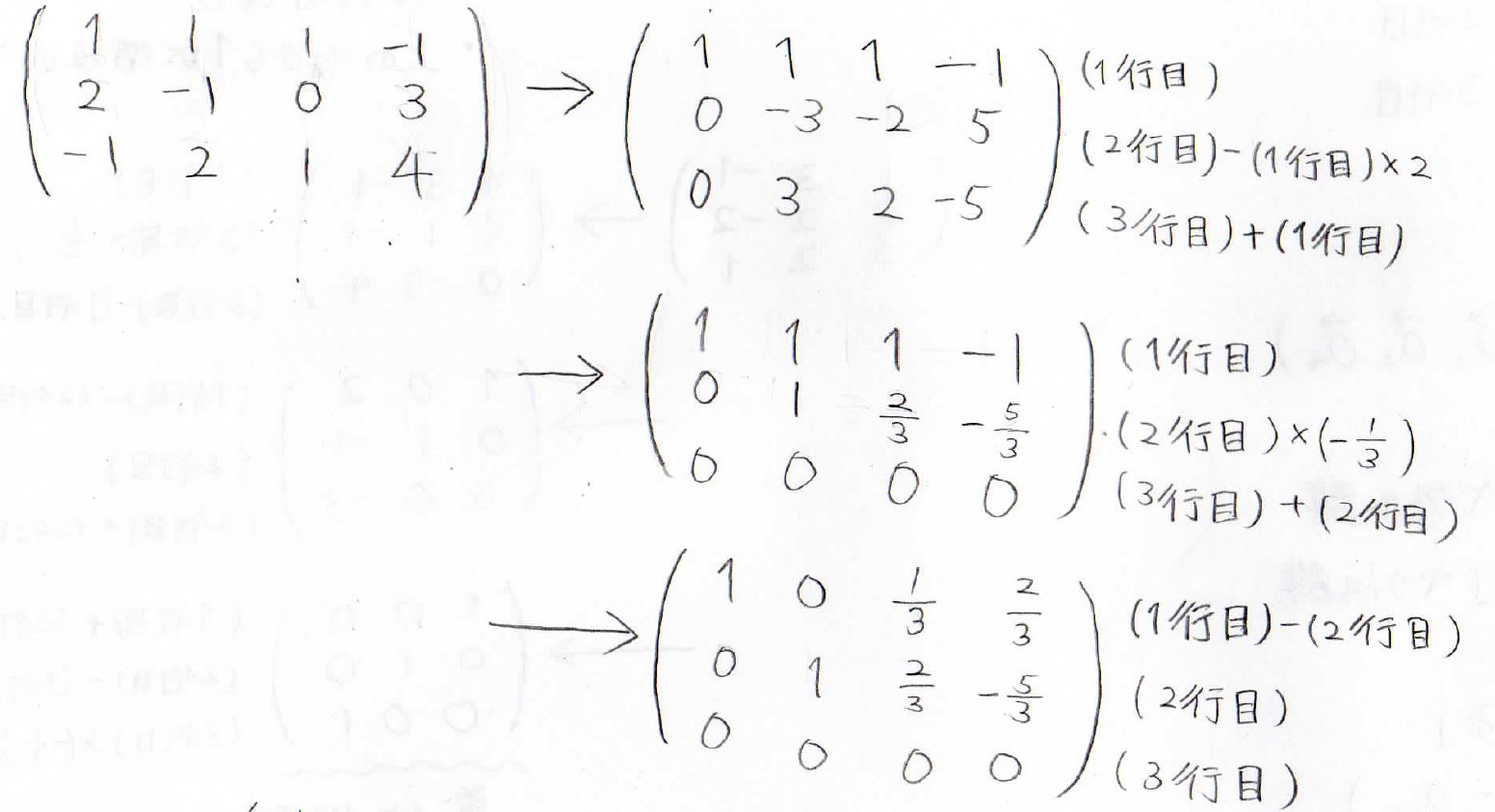
最終的に得られた行列は、3行目だけすべての成分が\(\displaystyle 0\)となっているため、そのランクは\(2\)となり、元の行列のランクも\(2\)だとわかります。
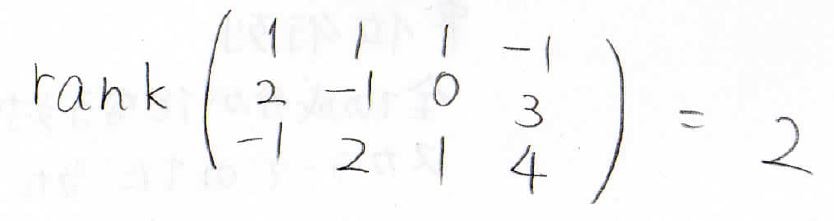
まとめ
はい、今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!
どうもありがとうございました!




