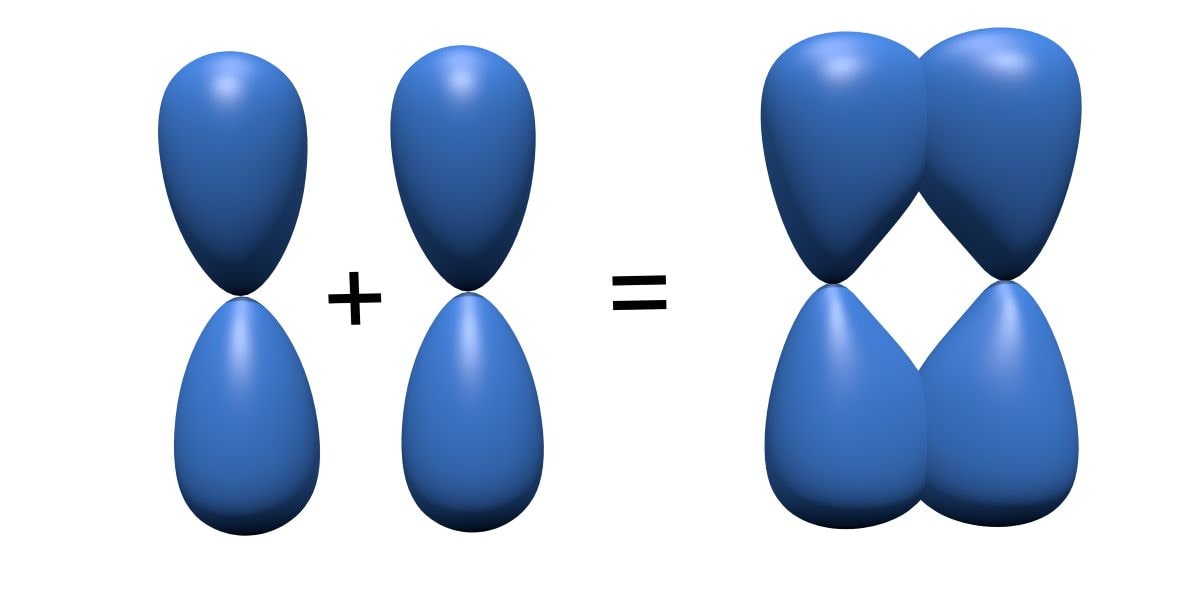こんにちは!
それでは今回も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(covalent bond)
なぜ電子を共有すると結合ができるのかということは、共鳴積分のところで説明してきましたが、今回はもっと詳しく見ていこうと思います。
共鳴積分については水素分子イオンと水素分子についてお話しした記事をご覧ください。

それでは、内容に入っていきます。
結合性軌道と反結合性軌道
まず、共有結合とは、2つ以上の原子核が電子を共有することで形成される結合のことを言います。
高校でもそれは習いますが、なぜ電子を共有すると結合ができるのかという説明はされなかったと思います。
1個の電子が2つの核に拘束されると、原子のときのエネルギーを基準に2つの効果が現れます。
その効果がクーロン積分と共鳴積分です。
詳しくは、水素分子イオンの記事でお話ししてますが、簡単におさらいしておくと、クーロン積分は新たに原子核が増えたことで電子との間にはたらく静電引力を反映しています。

これに対して、共鳴積分は静電相互作用が関係なく、量子が交換されることで安定化するという、量子力学特有の効果であす。
これらの効果を考えた結果、このようなグラフが得られます。
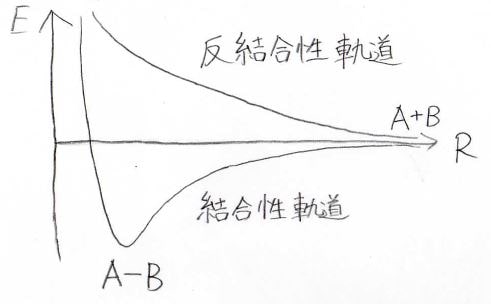
横軸が核間距離、縦軸が結合ができる前の値を基準としたエネルギーです。
エネルギーを求める過程でニ次方程式が出てくるので、解が2つ出てきます。
これらの状態には名前がついていて、単調減少しているほうを反結合性軌道、もう一方の非調和な振動ポテンシャルとなるほうを結合性軌道といいます。
では、順番に説明していきます。
結合性軌道
結合性軌道は、共有結合ができたことによる安定化がどれくらいかを表します。
ポテンシャルの極小が小さいほど、その結合は安定だと言えます。
また、一般的にはエネルギーが極小となる平衡核間距離が小さいほど安定な結合となります。
水素分子を例にすると、このように\(1\rm{s}\)軌道どうしが同じ位相となって重なることで、この状態となります。

この結合様式は対称であり、対称を指すドイツ語でgerade(ゲラーデ)というので、知っておいてください。
反結合性軌道
反結合性軌道は、結合の解離を理解する上でとても重要になります。
熱や光によってエネルギーを受け取った電子は、結合性軌道から反結合性軌道に移ります。
しかし、反結合性軌道はエネルギーが高く不安定です。
このポテンシャルカーブは核間距離に対して単調減少するため、より安定な状態になるためには核間距離が大きくなっていく必要があり、再び結合性軌道に戻らなければ、結合が切れてしまいます。
このように、反結合性軌道はエネルギーの吸収、分解、反応機構の理解などに必要な概念です。
水素分子を例にすると、下図のように2つの\(1\rm{s}\)軌道が逆位相で近づいた状態となっており、2つの核の中心には波動関数の位相が反転する節があります。

節では電子の存在確率は\(0\)となるので、この場合は、中心に電子は存在しません。
一般的に、節の数が多いほど不安定になるので、ぜひ知っておいてください。
同核、異核での共有結合におけるポテンシャルの違い
また、平衡核間距離におけるポテンシャル図は、同じ元素間と異なる元素間で、少し形が変わるので、それもお話ししておきます。
同核の場合は、結合性軌道の安定化と反結合性軌道の不安定化は、ほとんど同じくらいになります。
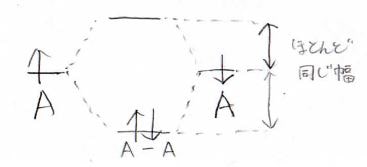
異核の場合は、そもそも結合を作る前の状態でエネルギーに差がありますが、結合性軌道は2つの原子のうちエネルギーが低いほうに近いものになります。
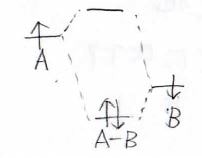
反対に、反結合性軌道はエネルギーの高いほうに近くなります。
エネルギーが近いということは構造が似ていると考えるのが自然なので、電子が一方の原子核側に少し偏在している構造が安定だと考えられます。
電気陰性度という言葉を使うとイメージしやすいと思います。
共有結合の種類
続いて、共有結合の種類を見ていきましょう。
先述のとおり、一般的に節の本数が多くなるほど、その軌道はエネルギー的に不安定になります。
節の本数で軌道の形状を分類すれば、その結合様式による安定化の度合いがだいたいわかります。
以後、説明のために、結合を作る2原子は\(x\)軸上にあるとしてお話しします。
\(\sigma\)結合
最も強い共有結合は、\(\sigma\)(シグマ)結合と言います。
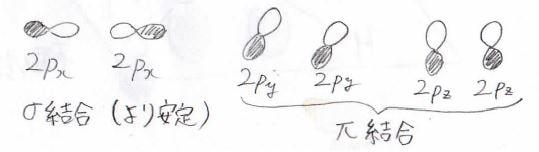
\(\sigma\)結合の例は、\(\rm{s}\)軌道どうし、\(\rm{s}\)軌道と\(\rm{p}\)\(_x\)軌道、\(\rm{p}\)\(_x\)軌道どうしなどで形成される共有結合です。
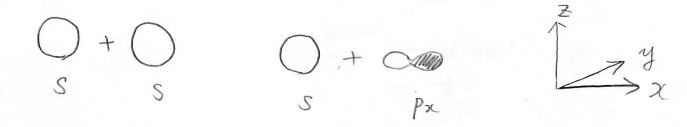
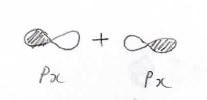
これらを\(x\)軸方向から見たときに節はなく、これが最も安定化の効果が大きいです。
\(\pi\)結合
次の結合様式は、\(\pi\)(パイ)結合です。
これは\(\rm{p}\)\(_y\)軌道どうし、\(\rm{p}\)\(_z\)軌道どうし、\(\rm{d}\)\(_{zx}\)軌道と\(\rm{p}\)\(_z\)軌道などの組み合わせでできる結合です。

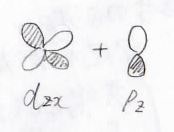
いずれも\(x\)軸方向から見たときに、\(y\)軸と\(z\)軸のいずれかが節となる形をしており、\(\sigma\)結合よりは弱い結合になります。
\(\delta\)結合
そして、節が2本となるものは、\(\delta\)(デルタ)結合と言います。
これは\(\rm{d}\)\(_{yz}\)軌道どうしなどで形成される結合を指します。
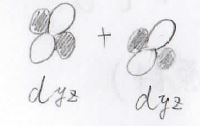
\(\sigma\)結合、\(\pi\)結合に比べると弱い結合になります。
実際にある分子を考えてみよう!
最後に、以上のことを踏まえて、実際にある分子に言えることを考えていきます。
窒素分子の三重結合
始めに、窒素分子の三重結合を考えてみましょう。
窒素原子の電子構造は、下図のように3つの\(2\rm{p}\)軌道に1つずつ電子が入っています。

希ガス構造となるためには、これら3つの電子を出し合って共有結合を作ることになります。
仮に、\(\rm{p}\)\(_x\)どうしで\(\sigma\)結合を作る場合、\(\rm{p}\)\(_y\)と\(\rm{p}\)\(_z\)は平行な形で結合を作るしかありません。
その結果、三重結合のうち1本は\(\sigma\)結合、2本は\(\pi\)結合だということになります。
そして、ポテンシャル図はこのようになります。
\(\sigma^\ast\)、\(\pi^\ast\)はそれぞれの反結合性軌道を指しています。
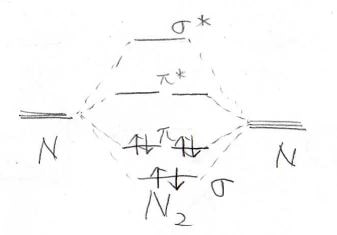
アミド結合(ペプチド結合)
次に考えるのは、アミド結合です。
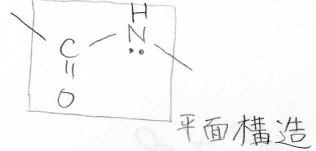
アミノ酸どうしで形成されるアミド結合は、ペプチド結合と呼びます。
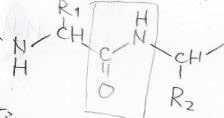
この結合は、\(\rm{C-N}\)単結合よりも強いことが知られており、ナイロンやタンパク質の力学的な強度や安定性を支えています。
この結合において、\(\rm{C}\), \(\rm{O}\), \(\rm{N}\), \(\rm{H}\)は同一平面上にあります。
この平面を横から見ると下図のようになっており、平面から垂直な方向に窒素原子の\(\rm{p}\)軌道があります。
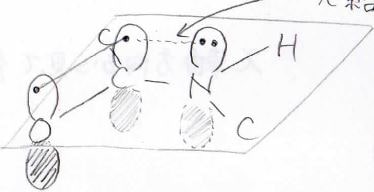
炭素原子と窒素原子それぞれの\(\displaystyle \rm{p}\)軌道どうしは直交しておらず、\(\displaystyle \pi\)結合と同じ位置関係であることから、安定化が起こります。
現実には、電子が非局在化することで、さらなる安定化が起こります。
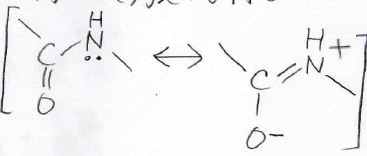
共鳴についてはこちらの記事をご覧ください。
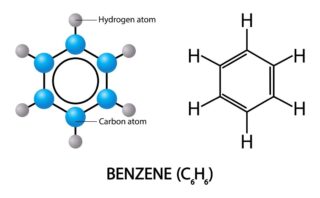
ブタジエン
同じことは、ブタジエンにも言えます。
これは合成ゴムの原料としてよく知られている物質です。
ブタジエンの構造は下図のとおりで、二重結合が2つあって、真ん中の結合だけが単結合となっています。
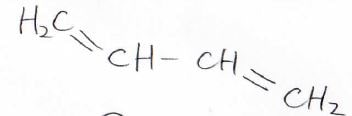
しかし、中央の単結合は、普通の\(\rm{C}\)\(-\rm{C}\)結合よりも強い結合であることが知られています。
その理由は先ほどと同じで、すべての炭素原子が同一平面上に位置して、\(\rm{p}\)軌道どうしで2つの\(\pi\)結合を作っています。
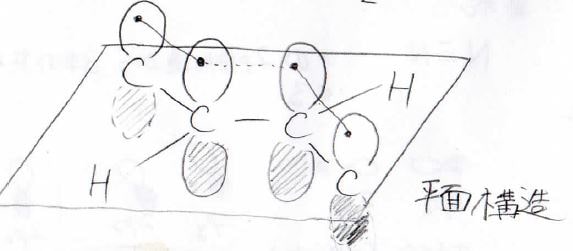
この際、2番目と3番目の炭素原子についても平行な軌道同士で\(\pi\)結合のような相互作用が起こるため、普通の単結合より安定な結合となります。
以上のように、平面に垂直な\(\rm{p}\)軌道間では、\(\pi\)結合のような安定化が起こり、一般的な単結合よりも強い結合となることがあります。
構造式で見れば単結合でも、実態は異なるということがありますので、平面になっていることをイメージすることが、その安定性を理解するためには必要になってきます。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!