こんにちは!
それでは今日も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(electronic spectrum of polydiatomic molecules)
それでは内容に入っていきます!
\(\displaystyle \rm{d}\)金属錯体
まず、\(\rm{d}\)金属錯体についてですが、過去にすでにお話ししていることも多いので、ここでは八面体錯体を例にさわりだけやっていきます。
詳しくは、こちらを参照してください。

本来の原子軌道では、すべての\(\rm{d}\)軌道が縮退していますが、これらが配位子の軌道と相互作用すると、静電的な相互作用の違いから、分裂が生じます。
\(x\)、\(y\)、\(z\)軸上に6個の配位子がある八面体錯体で考えると、\(\rm{d}\)\(_{x^2-y^2}\)軌道と\(\rm{d}\)\(_{z^2}\)軌道は軸の方向に電子が分布しているため、静電反発が大きく、ほか3つの\(\rm{d}\)軌道よりも不安定となります。
その結果、\(\rm{d}\)軌道は図のように分裂します。
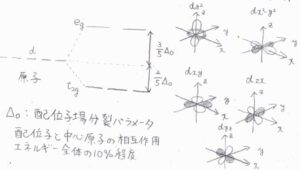
このエネルギー差は、中心原子と配位子の相互作用エネルギー全体の\(10\%\)程度であり、紫外-可視領域にある波長の電磁波を吸収することになります。
本来、\(\rm{d-d}\)遷移は\(\rm{g}\leftarrow \rm{g}\)の遷移であるため、ラポルテの選択律より禁制遷移となりますが、分子の非対称的な振動とカップリングすることで一部許容されます。
また、紫外線や可視光を吸収する別の機構として、配位子と中心原子間で電子が移動する電荷移動遷移もあります。
いちばん有名なのは、過マンガン酸イオンです。
水溶液は紫色を呈しますが、これは酸素原子からマンガン原子へと電子の移動が起こるためです。
電荷移動が起こる錯体は、電荷移動錯体や電子受容-供与錯体と呼ばれます。
さらに、配位子から金属原子へと電子が移動する錯体をLMCT錯体、金属原子から配位子へと電子が移動する錯体をMLCT錯体と言います。
電荷移動は、1つの原子内で電子が移動するよりも長い距離を移動するため、遷移双極子モーメントは大きくなり、スペクトル線の強度も強くなると考えられます。
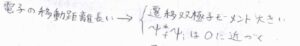
ただ一方で、被積分関数は遷移前後の波動関数の積で決まるため、移動距離が長くなるほど軌道の重なりが小さくなり、スペクトル線の強度は弱くなります。
軌道がまったく重なっていないときには、遷移双極子モーメントの大きさが\(0\)となるため、禁制遷移となります。
現実では、これらのバランスによって、強弱が決まることになります。
円偏光二色性(CD)
次に、入射光に偏光を用いた吸収スペクトルの話をします。
エナンチオマーの関係にある2種類の化合物に無偏光を照射して得られる吸収スペクトルにはほとんど差がありませんが、円偏光では差が生じます。
これを円二色性もしくは円偏光二色性と呼び、略してCDとも言います。
そもそも偏光の様式にはいくつかあり、一般的には楕円偏光を考えます。
これは、光線の進行方向に対して、電場ベクトルないし磁場ベクトルの先端が図のようならせんを描くものです。

ベクトルの大きさも周期的に変化するため、ある地点で電場ベクトルの先端の軌跡を書くと楕円になります。
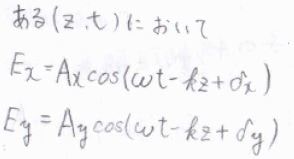
この楕円偏光の特別な例として、直線偏光や円偏光があります。
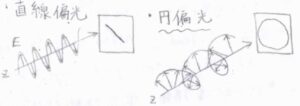
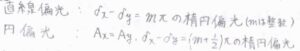
直線偏光は、電場ないし磁場の振動面が1つに限られているもので、かつては旋光度測定に用いられていました。
直線偏光は進行方向に垂直な二方向について、電場の位相差が\(m\pi\)と書ける楕円偏光と言えます。
ここで、\(m\)は整数です。
円偏光は、電場ベクトルの先端が円を描くものです。
これは、進行方向に垂直な二方向について、電場の振幅が同じ大きさで、かつ位相差が\(\displaystyle (m+\frac{1}{2})\pi\)と書ける楕円偏光と言えます。
さらに円偏光は、時計回りと反時計回りの2通りを考えることができます。

これらは、互いに二方向の位相差を\(\pi\)だけずらした関係です。
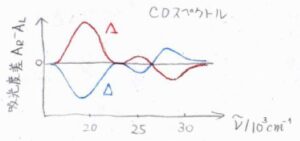
入射光に回転方向の異なる2種類の円偏光を用いると、キラルな分子で吸収スペクトルに差が生じるため、そこからこちらに示したようなCDスペクトルが得られます。
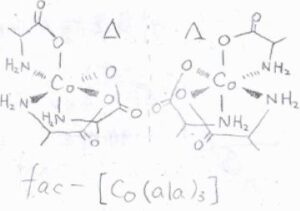
上図は、fac-トリス(アラニナト)コバルト(III)錯体の鏡像対となる2種類の分子に対して、CD測定を行ったものです。
縦軸が、右回りと左回りの円偏光を照射したときの吸光度の差で、横軸が吸収波数です。
2つのスペクトルは、\(A_\rm{R}\)\(-A_\rm{L}\)\(=0\)を基準に鏡写しの関係になります。
このCDスペクトルは、キラルな化合物の絶対立体配置を経験的、非経験的に求めるために役立つほか、タンパク質の二次構造、つまり\(\alpha-\)ヘリックスや\(\beta-\)シート、無秩序などの構造の割合を予測することに使われています。
また、CDスペクトルが得られれば、旋光分散スペクトルを計算によって得ることができるため、現在、旋光度測定をすることはあまり多くありません。
発色団
続いて、発色団というものについてお話しします。
多原子分子においても、ごく一部の構造によって吸収波数がだいたい決まることがよくあります。
特有の光学吸収を有し、可視光を吸収する場合には色の原因となる原子の集団のことを発色団と言います。
厳密な吸収波数は、発色団ではない部分に依存します。
こちらに示したのが発色団の一例です。
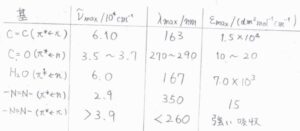
\(\tilde{\nu}_\rm{max}\)、\(\lambda_\rm{max}\)、\(\varepsilon_\rm{max}\)は、吸収ピークを与える波数と波長、そして、強度から算出したモル吸光係数を指します。
例えば、アゾ化合物には赤色や朱色っぽい色をもつものが多くありますが、これはアゾ基があることによって、紫外領域に強い吸収帯をもつほか、青色の光を少し吸収するようになるためです。
1つの発色団が与える吸収ピークは1本と限らず、また、吸収の強度には3桁ほど差が生じることもあります。
\(\pi^\ast\leftarrow \pi\)遷移と\(\pi^\ast\leftarrow \rm{n}\)遷移
最後に、発色団活性の原因となる電子遷移の機構について、お話しして終わります。
先ほどの表の中で、モル吸光係数がとる値は、4桁くらいの広い領域に及ぶことを示しましたが、これは許容遷移と禁制遷移の違いです。
まず、\(\pi\)軌道から活性な\(\pi\)軌道への遷移は、\(\pi^\ast\leftarrow \pi\)遷移と呼ばれ、許容遷移のため、強い吸収ピークを与えます。

非共役二重結合では、吸収波長は典型的に\(180\ \rm{nm}\)程度の値となります。
これは、紫外領域に相当するため、色の原因にはなりにくいですが、共役系に含まれる二重結合では、その長さによって吸収波長も長くなるため、可視光を吸収することもあります。
対して、こちらの\(\pi^\ast\leftarrow \rm{n}\)遷移は禁制遷移となるため、弱い吸収ピークとして観測されます。

この遷移は、孤立電子対に由来しています。
分子軌道法において、\(\rm{n}\)は結合形成にほとんど関与しない軌道のことを指します。
カルボニル基の吸収波長は\(290\ \rm{nm}\)程度なので、まだ可視光ではないですが、アゾ基では青色の光を吸収するため、補色である朱色に近い色を示すことになります。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!




