こんにちは!
それでは今回も化学のお話やっていきます。
今回のテーマはこちら!
動画はこちら↓
動画で使ったシートはこちら(first law of thermodynamics)
内部エネルギーの意味
まずは、内部エネルギーの意味についてお話しします。
化学の言葉で、考察の対象とする部分を表すときに、「系」という言葉を使いますが、内部エネルギーとは、その系内の全エネルギーを指します。
絶対温度\(T\)における理想気体の内部エネルギー\(U(T)\)は、\(0\ \rm{K}\)における内部エネルギー\(U(0)\)と温度に比例する熱運動のエネルギーの和で書けます。
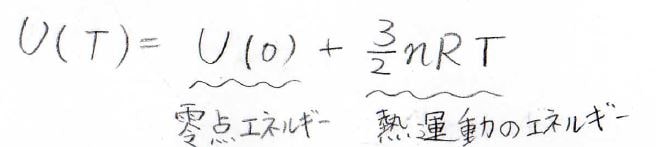
ここで、\(\displaystyle n\)は物質量、\(\displaystyle R\)は気体定数です。
熱運動のエネルギーが\(\displaystyle \frac{3}{2}nRT\)となるのは、分子が並進運動しかしていないときです。
すなわち、気体分子が単原子分子のとき、あるいは低温のときです。
\(U(0)\)は零点エネルギーとも呼ばれ、これは量子力学によって説明されます。
一次元井戸型ポテンシャルに閉じ込めた量子には、最安定状態においても\(0\)ではないエネルギーの値がありました。
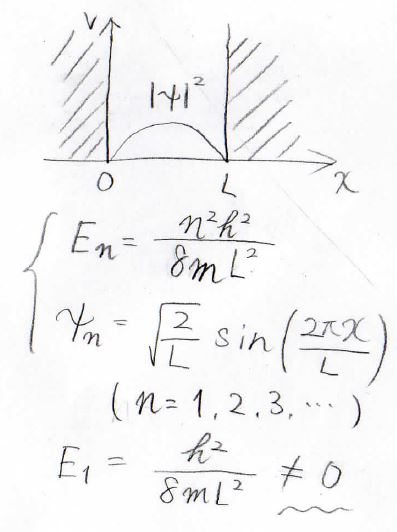
詳しくは、こちらの記事をご覧ください。

三次元の箱の中でも、これと同様に最安定状態のエネルギーは\(\displaystyle 0\)になりません。
多くの場合は、\(U(T)\)から\(U(0)\)を引いた、熱運動に帰属されるエネルギーだけを内部エネルギー\(U\)と表します。
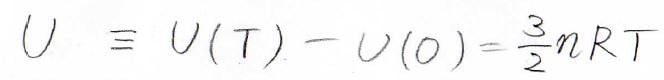
内部エネルギーが変化する要因
続いて、内部エネルギーを変化させる方法について考えてみます。
熱量
1つ目は、熱です。
系の外から熱を与え、分子の温度を上昇させます。
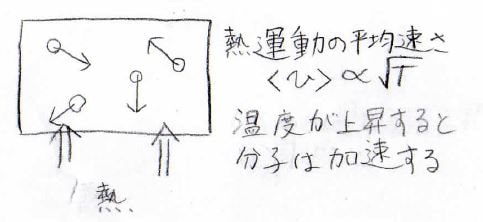
気体分子運動論やマクスウェル-ボルツマン分布で導かれるように、分子の平均の速さは、絶対温度の平方根に比例します。
つまり、温度が上昇することは分子の運動が速くなることと同じであり、内部エネルギーも温度に比例して増大します。
詳しくは、こちらを参照してください。
仕事
そして、2つ目の方法は、仕事です。
例えば、系の外から上方向へ力が与えられ、系の体積が変化したとします。
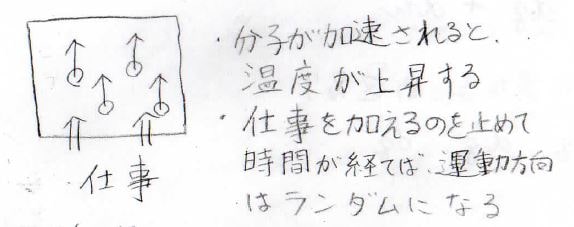
仕事をされている最中と終わった直後には、分子が壁から一方向への力を受けることで、上方向へ加速します。
この場合は、分子が加速されることが温度の上昇につながって、内部エネルギーの増大も起こります。
ちなみに、仕事をやめて少し時間がたてば、分子どうしの衝突により、運動の方向はまたランダムになります。
熱力学第一法則
以上の説明を式にすると、次のようになります。

内部エネルギーの変化量\(\Delta U\)は、系に与えられた熱量\(q\)と系がされた仕事\(w\)の和で表せます。
これは熱力学第一法則と呼ばれ、熱力学の重要なルールの1つになります。
この式から言えることは、まず孤立系、すなわち外部から熱も加えられず、仕事もされない場合には、内部エネルギーは一定になります。
熱量や仕事はエネルギーと同じ単位をもちますが、エネルギーとまったく同じものではなく、エネルギーが移動するときの形に過ぎません。
例えば、食べ物の熱量の単位は\(\rm{kcal}\)ですが、あれは食べ物を分解することで発生する熱量のことで、人に外部から与えられる化学エネルギーの大きさを指しています。
そして、この第一法則は、第一種永久機関ができないことを示しています。
第一種永久機関とは、外部から熱も仕事も加えることなく、外部へ仕事をする装置のことです。

化石燃料のエネルギー問題が一切発生しない夢の機械ですが、熱力学第一法則により、実現不可能であると言えます。
ちなみに、第二種永久機関もありますが、これは第一法則に反しないように、装置の中で仕事をする部分を組み入れたものです。
これは、熱力学の第二法則より、仮に作れたとしても役に立たず、エンジンなどのような使い方はできないとされています。
熱力学第二法則については、こちらを参照してください。

状態量と非状態量
最後に、状態量という言葉を紹介します。
状態量とは、系の状態だけで一意的に決まる量のことを言います。
それはつまり、過去の履歴や変化の経路には依存しない量とも言い換えられます。
グラフで説明すると、次のようになります。
まず、ある温度\(T_1\)の理想気体が\(p\)-\(V_\rm{m}\)グラフ上の点Aにあったとします。

そこから温度\(T_2\)の点Bへ変化させるとき、①と②の2通りの経路を通ったとします。
温度の変化量は同じであるため、内部エネルギーの変化量も等しくなります。
しかし、気体に与えられた熱量や仕事は同じにならず、経路に依存します。
内部エネルギー\(U\)は、\(p\)と\(V_m\)という状態を表す物理量の関数になるため、状態関数とも言います。
反対に、\(p\)や\(V_m\)も\(U\)の関数となります。
そして、\(p\)や\(V_m\)だけではその値が決まらず、変化の経路に依存する熱量や仕事は、経路関数と呼ばれます。
熱力学では、微小変化量を使って考えることが多いのですが、そのときにこの状態量と非状態量は明確に区別して、表記します。
例えば、内部エネルギーの微小変化量\(\rm{d}\)\(U\)は、下のように書きます。

\(\rm{d’}\)や\(\delta\)と書く場合もあります。
このブログでも、同様に書いていくので、この違いを頭に入れておいてください。
まとめ
今回の内容は以上です。
間違いの指摘、リクエスト、質問等あれば、Twitter(https://twitter.com/bakeneko_chem)かお問い合わせフォームよりコメントしてくださると、助かります。
それではどうもありがとうございました!